第七讲:素数算法优化:只需遍历1到根号n, 判断n%i==0
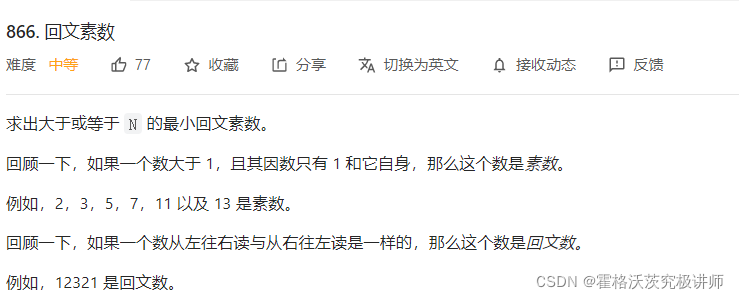
第一题
bool judgehuiwen(int n)
{
int temp;
int hui;
int old=n;
if(n<10)
{
return true;
}
while(n!=0)
{
temp=n%10;//末尾
n=n/10;
hui=hui*10+temp;
}
if(old==hui)
{
return true;
}
return false;
}
int judge_sushu(int n)
{
int j, sqrtn = sqrt(n + 1e-6);
for (j = 2; j <= sqrtn; j++)
{
if (n % j == 0)
return 0;
}
return 1;
}
int primePalindrome(int n){
for(int i=n;i<=2*(1e+8);i++)
{
if(judge_sushu(i))
{
if(judgehuiwen(i))
{
return i;
}
}
}
return 0;
}
我的思路:从n开始遍历,先检查是否是素数,再检查是否是回文数
检查素数从1到根号n遍历
检查回文数将数字翻转输出,可惜翻转后的数字overflow了
或者将数字换成字符串后翻转
运用函数itoa(number,存放的数组,几进制)
第二题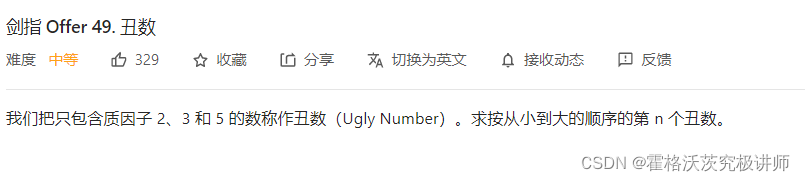
思路一:动态规划(三指针)指针即数组下标
1 2 3 4 5 6 8 9 10 11 12
观察丑数可知,丑数都是由2 3 5 乘出来的,所以丑数数组可以分为三个数组
1.由前数乘2出来的
2.前数乘3出来的
3.前数乘5出来的
由于从哪个数开始乘都一样,所以我们可以从第一个数1开始乘
因此开始归纳动态规划
状态定义:dp[n]是第n+1个丑数
状态转移方程:dp[i]=min(dp[a]×2,dp[b]×3,dp[c]×5)
初始状态:dp[0]=1
返回值:dp[n]
由于在乘的过程中三个数组会产生重复数,所以
单独判断如果是2指针乘出来的就2号指针++,3号就3号++,而不是算一次dp[n]就所有指针++
int min(int a,int b)
{
return a<b?a:b;
}
int nthUglyNumber(int n){
int a=0,b=0,c=0;
int dp[1690];
dp[0]=1;
for(int i=1;i<n;i++)
{
dp[i]=min(min(dp[a]*2,dp[b]*3),dp[c]*5);
if(dp[i]==dp[a]*2)
{
a++;
}
if(dp[i]==dp[b]*3)
{
b++;
}
if(dp[i]==dp[c]*5)
{
c++;
}
}
return dp[n-1];
}
思路2:最小堆

第八讲:
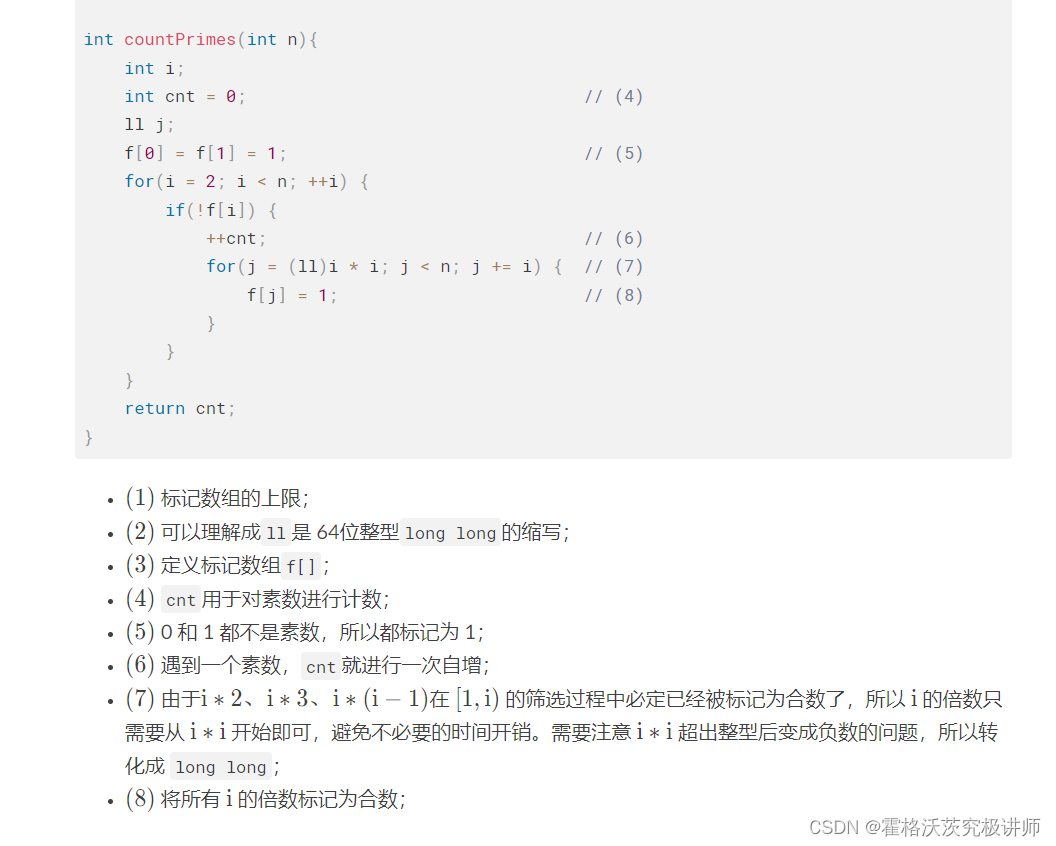
[1,\sqrt n][1,n] 范围内的素数可以通过筛选法预先筛出来,用一个数组 f[i]标记 ii 是素数与否,筛选法有很多,这里介绍一种最常用的筛选法——Eratosthenes筛选法。

1.定义标记数组
2.for(int i=0;i<n;i++)
{
if(!f[i])
{
for(int j=(long long)i*i;j<n;j+=i)
f[j]=1
第一题
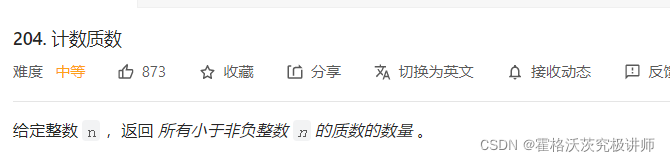
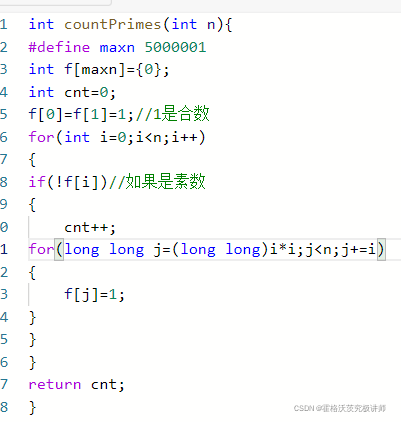
遍历1到n,如果是素数,就将素数的倍数都标记为1
为优化算法,j从i*i开始遍历,因为在之前的一定已经被标记过,到n为止(n为所给的数)





 本文探讨了素数算法的优化,通过Eratosthenes筛选法减少遍历次数,并结合动态规划解决回文数判断问题。介绍了如何利用1到根号n的遍历和三指针技巧,同时涉及了丑数的求解,展示了代码实例和优化思路。
本文探讨了素数算法的优化,通过Eratosthenes筛选法减少遍历次数,并结合动态规划解决回文数判断问题。介绍了如何利用1到根号n的遍历和三指针技巧,同时涉及了丑数的求解,展示了代码实例和优化思路。
















 85万+
85万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








