生活中,我们常常见到朋友圈有人偶尔装装逼,我挺赞赏的,很多人可能说了,越是牛逼的人,越是内敛,低调。实际上牛不牛逼,和低调不低调没有任何关系。现在不是孔融让梨的时代,不去争取机会,怎么能朝着自己的方向。实力装逼有时不是坏事。看下面这张图
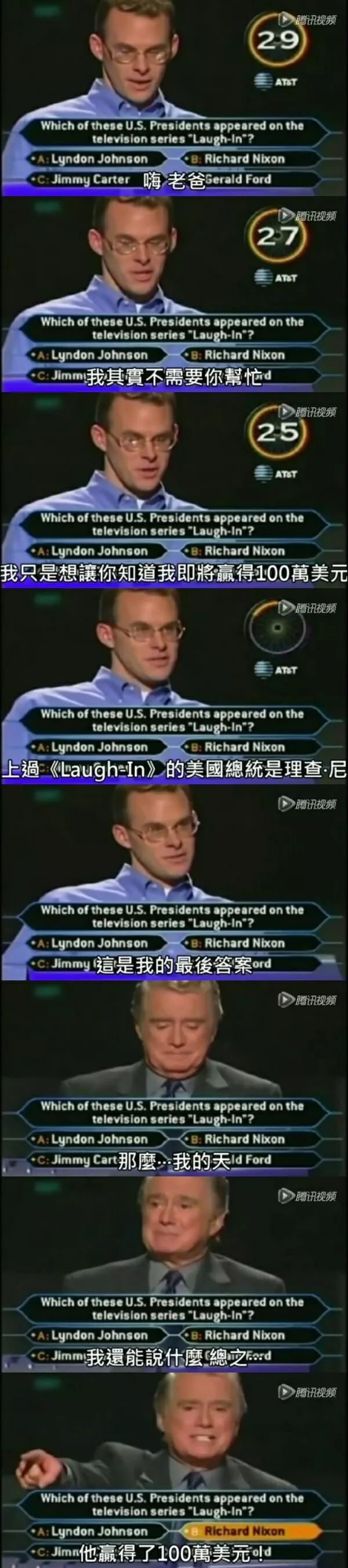
据说这是个真实的节目,这逼装的满分。可能是装逼史中立下一座供后人敬仰的丰碑了。

不说了,我也要去装个B了

生活中,我们常常见到朋友圈有人偶尔装装逼,我挺赞赏的,很多人可能说了,越是牛逼的人,越是内敛,低调。实际上牛不牛逼,和低调不低调没有任何关系。现在不是孔融让梨的时代,不去争取机会,怎么能朝着自己的方向。实力装逼有时不是坏事。看下面这张图

据说这是个真实的节目,这逼装的满分。可能是装逼史中立下一座供后人敬仰的丰碑了。

不说了,我也要去装个B了

 3万+
3万+
 2303
2303

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


