雷达覆盖问题,贪心算法。
题目来源:CSUST2012年8月暑假集训组队后第一场个人赛(貌似是8月7日)
原题链接:http://poj.org/problem?id=1328
Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 34841 | Accepted: 7737 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
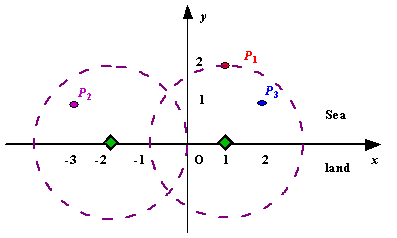
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
Source

注意:
计算左右交点时的精度问题,全部用double算,tmd 有小数
2013 暑假重做:
/*
2013-7-22晚重做code
题意:直角坐标系上方有 N 个岛屿,有一种雷达,可以覆盖半径为 d 的圆
现在在 X 轴上设置雷达,问最多修建多少个可以覆盖全部的岛屿
如果无法覆盖全部的岛屿,则输出 -1
算法:贪心
思路:1.以各个岛屿为圆心,雷达覆盖长度为半径作圆,记录与 X 轴的左右交点
2.按照各个岛屿与 X 轴的交点排序,先按照左交点从小到大排序,在按照又交点从小到大排序。
3.排序后从小到大依次遍历每个岛屿,如果有相交的区间,则用同一个雷达覆盖【同时注意缩小相交区间 [left最大的, right最小的]】,
否则另外增加一个雷达。【就和前面湖大那题一样。。。关于区间的处理】
*/
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int maxn = 1000+10;
struct Point
{
double x,y; //坐标
double left,right; //与 X 轴左右交点
}p[maxn];
bool cmp(Point a, Point b) //按照与 X 轴交点从左到右排序
{
if(a.left == b.left) return a.right < b.right;
else return a.left < b.left;
}
int main()
{
int n,d;
int test = 0;
while(scanf("%d %d", &n, &d) != EOF)
{
if(n == 0 && d == 0) break;
int ans = 0;
for(int i = 0; i < n; i++)
{
scanf("%lf%lf", &p[i].x, &p[i].y);
if(p[i].y > d) ans = -1; //一定无法满足覆盖
}
if(ans == -1) //输出无法满足的情况
{
printf("Case %d: %d\n", ++test, ans);
continue;
}
for(int i = 0; i < n; i++)
{
double s = sqrt(d*d-p[i].y*p[i].y);
p[i].left = p[i].x-s; // 与 X 轴左右交点
p[i].right = p[i].x+s;
}
sort(p,p+n,cmp);
ans = 1;
for(int i = 1; i < n; i++)
{
if(p[i].left <= p[i-1].right) // 与前面的相交区间
{
p[i].left = max(p[i].left,p[i-1].left); // 不断缩小区间
p[i].right = min(p[i].right,p[i-1].right);
}
else ans++;
}
printf("Case %d: %d\n", ++test, ans);
}
return 0;
}
2012 暑假总结
/******************************************
题意:给你一个直角坐标系;
在x轴上方给你n个小岛,再给出雷达的覆盖半径d;
当n和d为0时测试结束;
剩下n行,依次给出岛屿的坐标(测试数据是int型,注意double转换);
求在x轴上最少设置几个雷达,可以覆盖所有的岛屿,如果不能完全覆盖则输出结果为-1;
思路:1、已各个小岛小岛为圆心,以雷达覆盖半径为半径做园,记录与x轴的交点坐标(如果有交点则记录,如果有一个没有交点则表示不能完全覆盖);
2、根据各个岛屿与x轴的左右交点排序(先按照左交点从小到大排序,如果坐交点相同,则按照又交点从小到大排序);
3、那么经过上面的步骤后,各个交点区肯定会有相加范围,尽量在相加最多的范围设置雷达即可;
4、从左到右开始查找,设置一个点point为当前雷达覆盖指向的最右点,初始化为第一个圆的右交点;
5、如果下一个圆的重叠区的左交点大于当前point,雷达数目+1,并且把当前的圆的右交点赋给point;
6、如果下一个圆的重叠区的右交点小于当前point,说明它已经被覆盖,直接把它的右交点赋给point即可。
注意:由于要用到sqrt,所以要小心double型的转换。
***********************************************/
//Accepted 200K 16MS C++ 928B 2012-09-18 19:43:01
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct Node
{
double left,right;
}node[1010];//圆与x轴的交点
int cmp(Node a,Node b)
{//排序:先按照与x轴的左交点从小到大排,如果左交点相同再按照右交点从小到大排
return a.left<b.left || (a.left==b.left && a.right<=b.right);
}
int main()
{
int n;
int i;
double d;
double x,y;
int sum,ok,c=0;
double point;//记录当前雷达在x轴上覆盖区域的最右点
while(scanf("%d%lf",&n,&d)!=EOF && n)
{
ok=1;
if(d<0)//如果雷达覆盖半径<0,则不可能
ok=0;
for(i=0;i<n;i++)
{
scanf("%lf%lf",&x,&y);
if(y>d)//排除不可能情况
ok=0;
double tt=sqrt(d*d-y*y);//注意double的转换
node[i].left=1.0*x-tt;//记录左交点
node[i].right=1.0*x+tt;//记录右交点
}
if(ok==0)//如果不可能
{
printf("Case %d: -1\n",++c);
}
else
{
sort(node,node+n,cmp);
point=node[0].right;
sum=1;//设置第一个雷达
for(i=1;i<n;i++)//挨个岛屿查找
{
if(node[i].left>point)//如果当前查找的岛屿的最左边的覆盖范围都不在雷达的覆盖范围内
{
sum++;//建立新雷达
point=node[i].right;//以当前的岛屿的右交点赋给新建立的雷达的最右边的覆盖范围
}
else if(node[i].right<point)//当前岛屿的右交点都小于前面雷达覆盖位置,则说明已经被覆盖
point=node[i].right;//更新当前雷达覆盖范围
}
printf("Case %d: %d\n",++c,sum);
}
}
return 0;
}























 1186
1186

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








