4.2 图数据库
| 实验使用的数据库名称 | 描述 |
|---|---|
| MUTA | 全称mutagenicity,一共有4337个图,该图为无向图,并且顶点和边是有属性的。“突变”数据库中的图是化学分子的建模。在实验中,为了简化实验,减少比对的图的个数,从4337个图中抽样选取图分析。将抽样的图分成8个小组,除了最后一个小组外,每个小组图的顶点个数范围在10和70之间,并且每个小组都有是个图,第8个小组也有10个图,但是图顶点的大小是固定的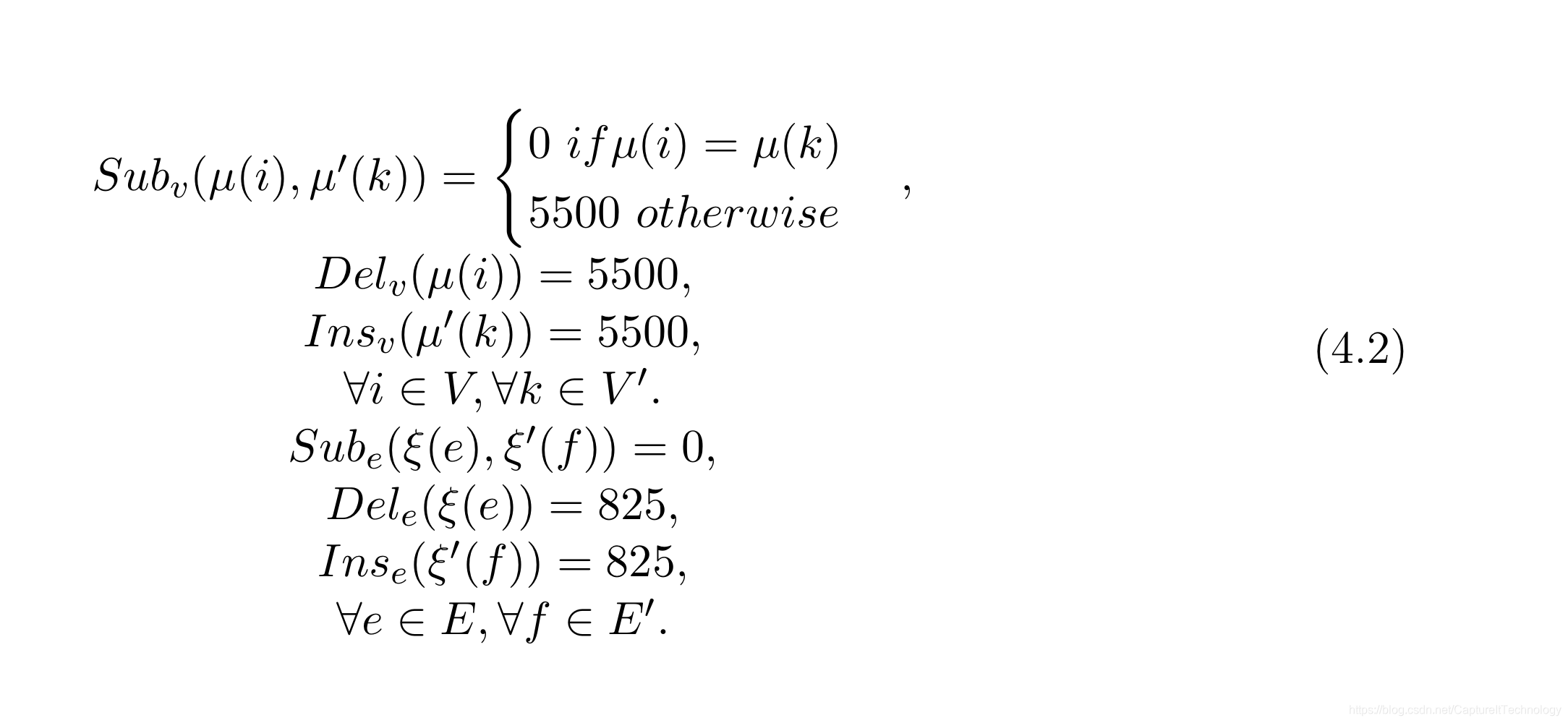 |
| PAH | 一共有94个图,对化学分子建模。每个图是无向图并且无属性的。每组图之间是比对的实例,共有8846组实例。比对的代价函数定义如下: 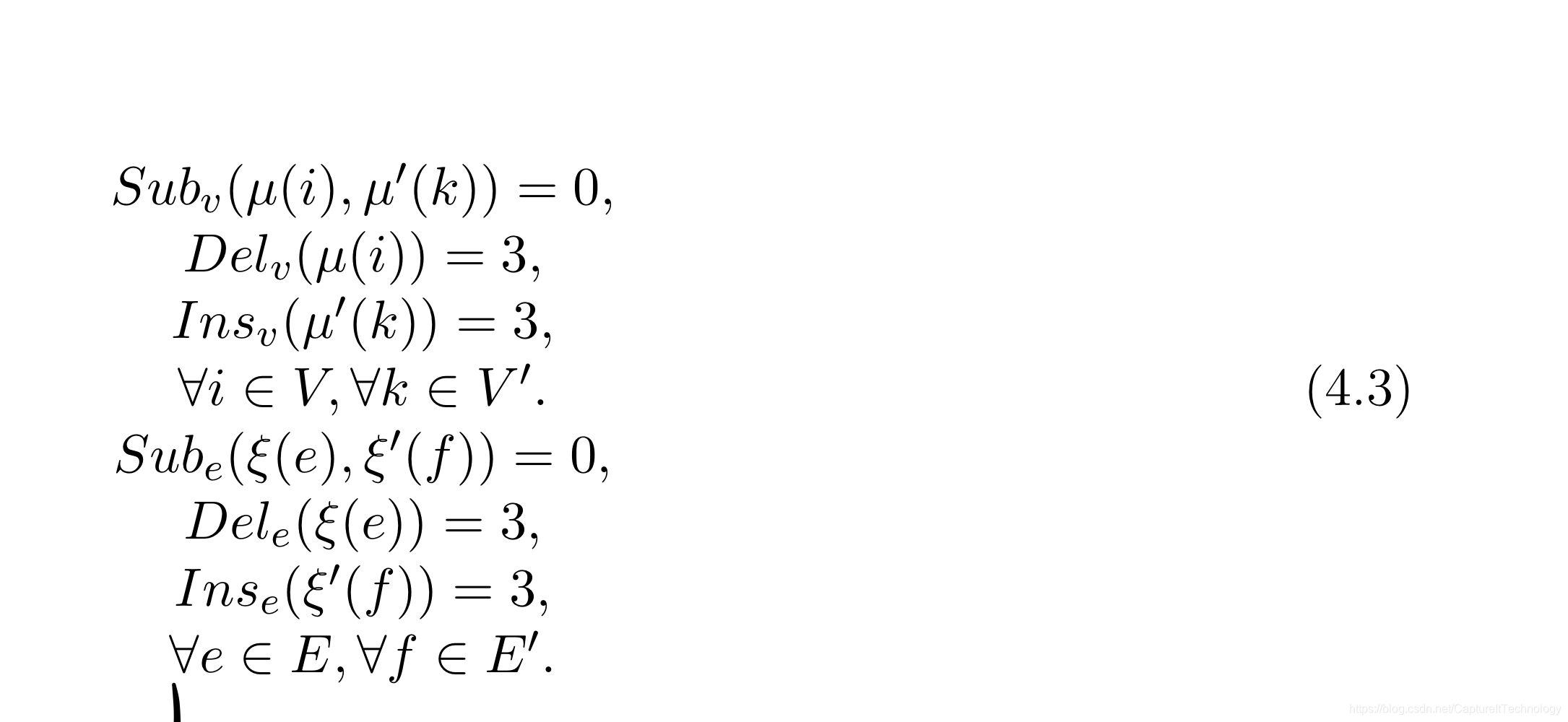 |
| CMU-HOUSE | 111个图,每个图代表了一个房间在不同角度的3D建模的图。每个图有30个顶点,但是每张图都代表的是同一个房间,不同的原因是旋转了房间的角度。每个图是有属性图,顶点的属性使用“Shape Context”的特征向量表示,边属性表示俩个入射点(incident vertices)的距离。该数据库提供了所有图对之间的真实匹配。因为这个数据库在图匹配领域应用广泛,因此代价函数分为三种:House-NA、House-A、House-REF,具体代价见表格后阐述。 House_NA: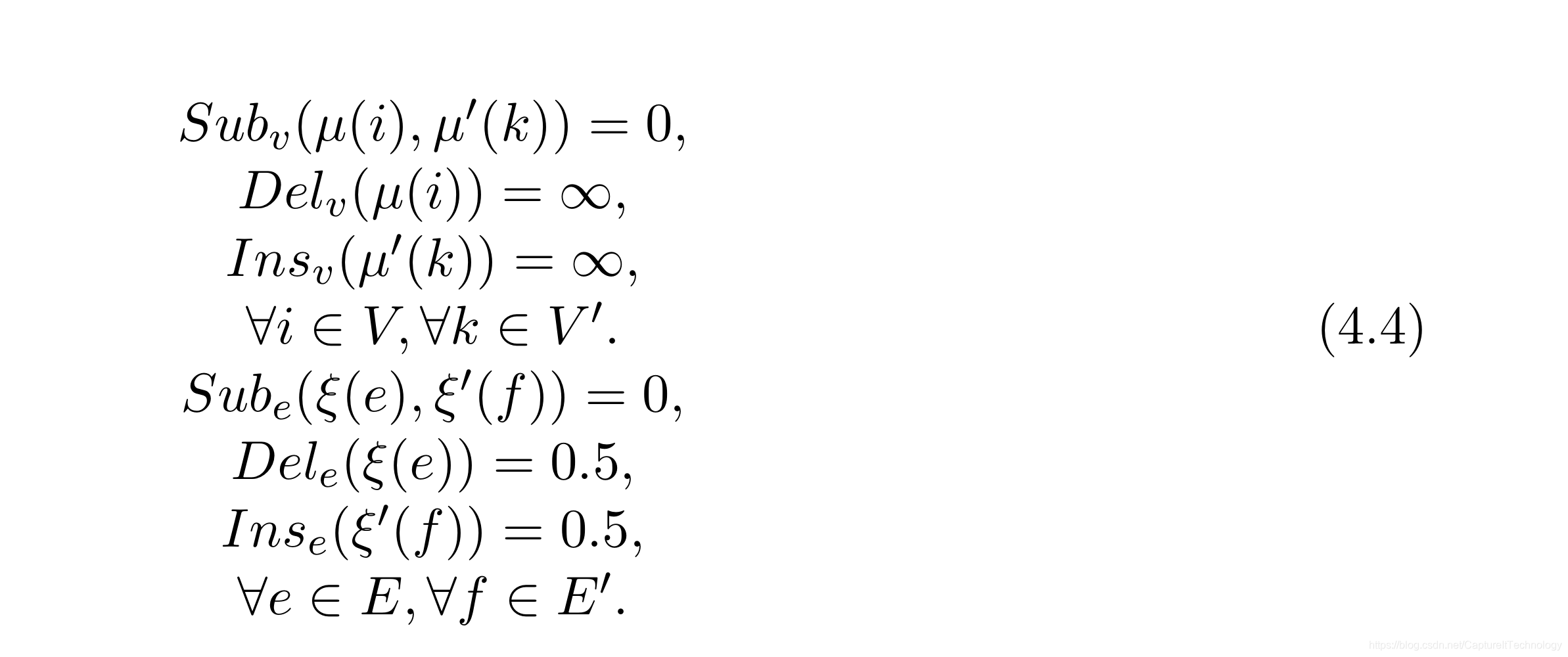 House_A: House_A: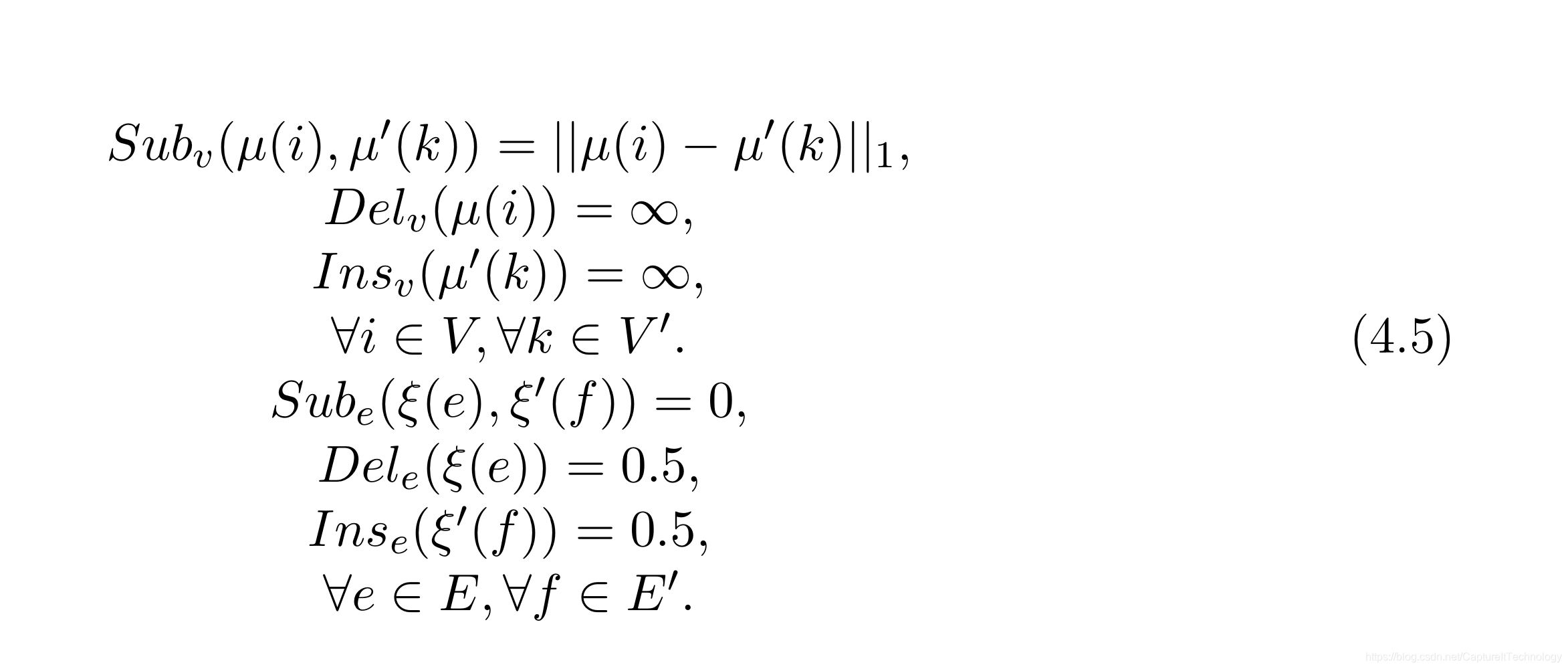 House_Ref: House_Ref: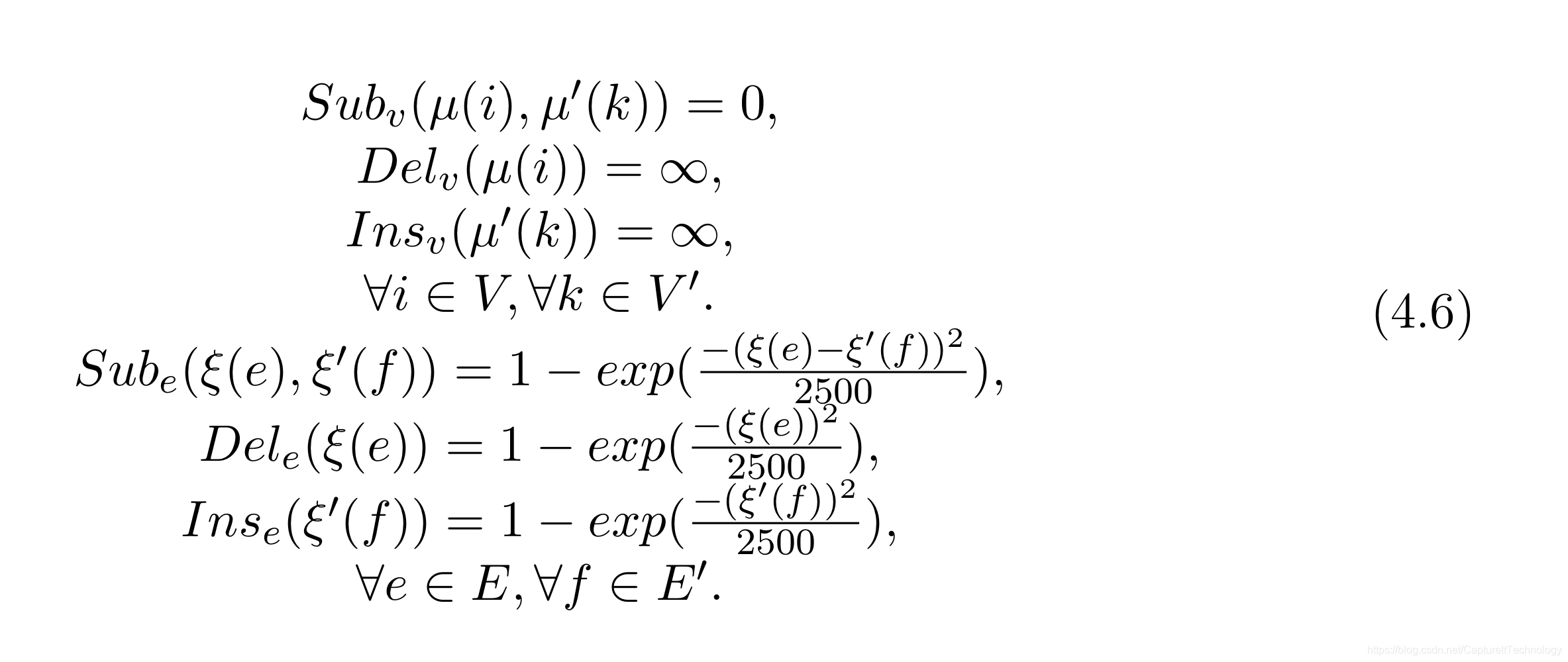 |
| CMU-HOTEL | 共101个图,和CMU-House相似,使用代价函数相同,不同之处这些图使用3D图像模拟酒店 |
| PALMPRINT | 对人的手掌进行建模,含有160个图。每个图的顶点个数大于800个,边2000个左右。每个图是属性图,表现在顶点有属性:每个顶点存储了图像的坐标,角度,类型等等,代价函数定义如下:。 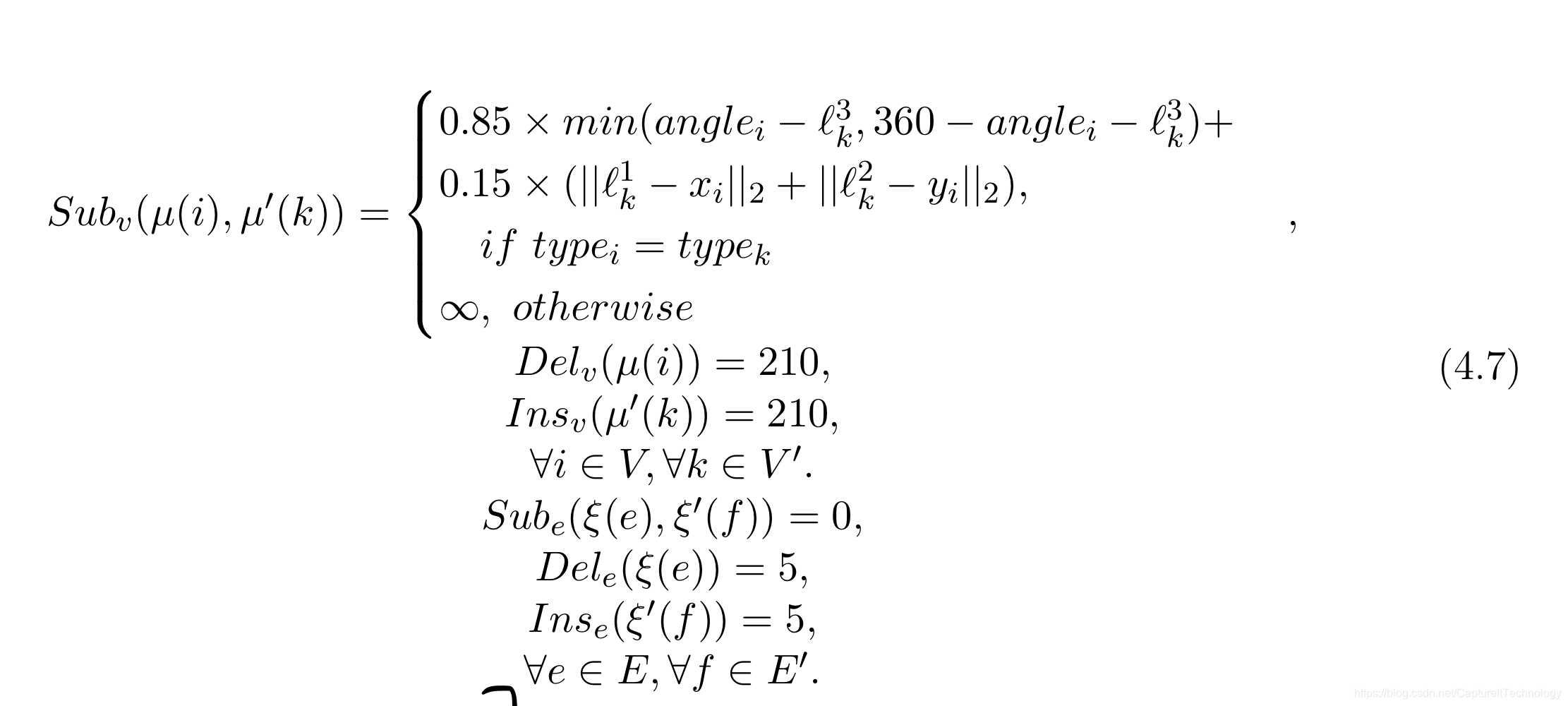 |
| VOC-CAR | 对图像中的汽车进行建模,属性图。边的属性:俩个顶点之间的距离ded_ede和俩个顶点之间的角度θf\theta_fθf ,代价函数如下: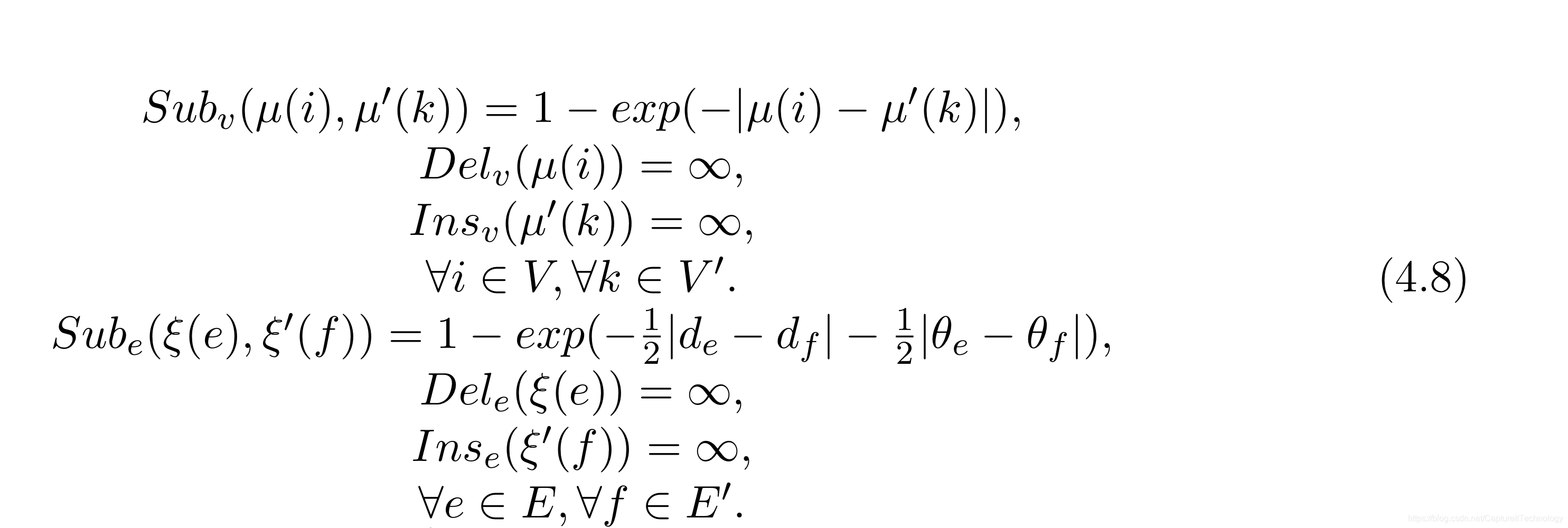 |
| VOC-BIKE | 440个无向。属性图,建模对象为自行车,代价函数上图所示。 |
| PROTEIN | 600个图,无向,有属性。顶点属性:类型、序列、序列长度;边属性:频次、一种类型或者多种类型、边的距离。举例:[freq:1,type0:1,distance0:17.1,type1:1,distance1:4.2....freq:1,type0:1,distance0:17.1,type1:1,distance1:4.2....freq:1,type0:1,distance0:17.1,type1:1,distance1:4.2....] 代价函数如下: |
| SYNTETHIC | 人工合成数据集,优点是可以控制图的密度(图中边个数和完全图边的占比)。图密度距离:如果一个图30个顶点,那么10%密度的图有多少条边?计算完全图边的个数为435条边,那么10%密度的图有43.5条边。人工生成30,100个顶点的数据集标记为:SYNTHETIC-30,SYNTHETIC-100。合成数据的目的是造出中等(30-70)和大规模(70个顶点)的图,并且在不同的GED的方法中应用这些数据,决定使用什么样的数据会使得GED的算法运行更加流畅。代价函数定义如下: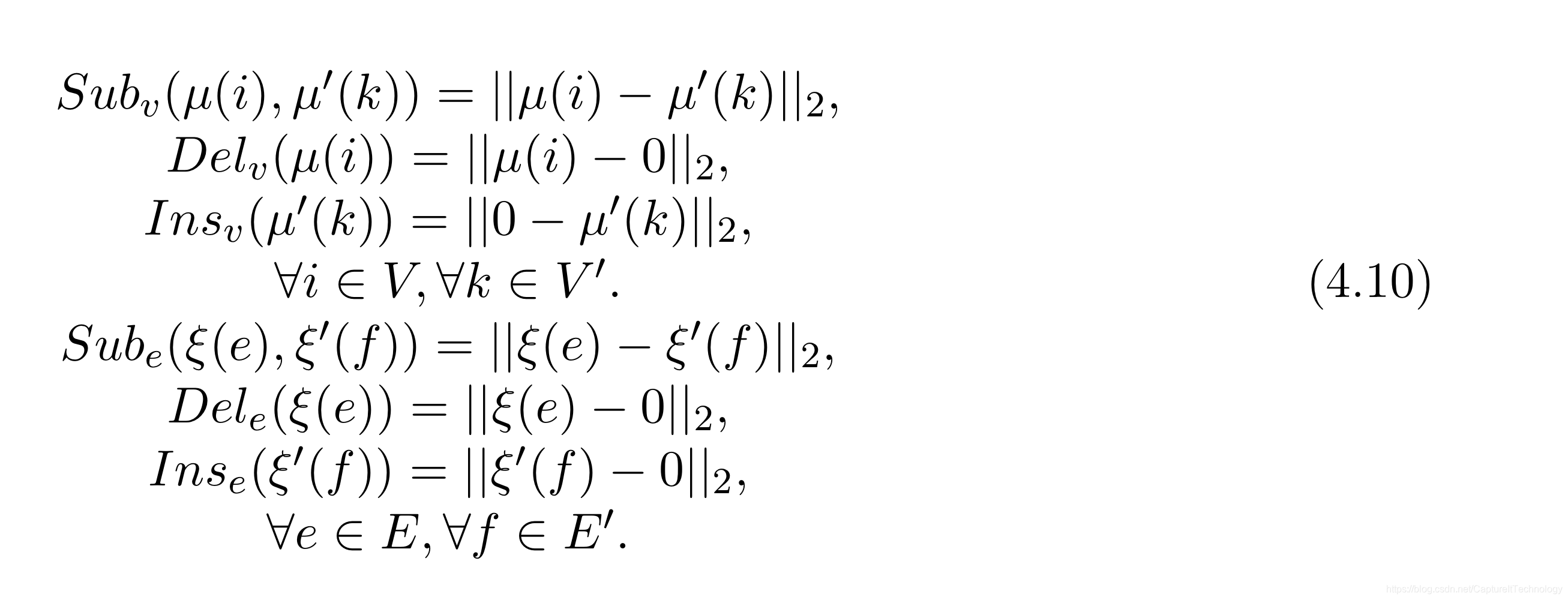 |
- 如何判断图数据库中的图是密集图还是非密集图?
答:如果边密度density>10,是密集图,否则是非密集图。下面是几种数据库中边密度。
| 图数据库名称 | 密度占比% |
|---|---|
| CMU | 18.00 |
| PROTEIN | 16.00 |
| VOC | 13.47 |
| PAH | 12.22 |
| MUTA | 9.13 |
| PALMPRINT | 0.77 |
图数据库中图格式:
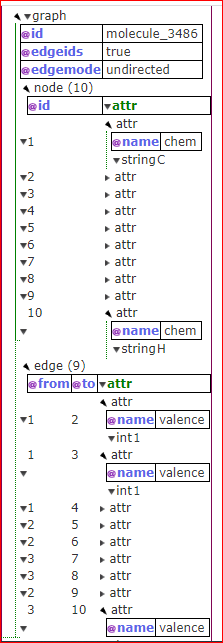
在进行俩个图之间顶点的比较时候,可以考虑到顶点的属性的值。通过考虑到属性值,来定义俩个顶点的相似程度,具体方法为:若顶点的属性可以表示成数值,可以使用L2范式(向量元素绝对值的平方和再开方)或者欧几里得距离(俩个不一样吗? 来源:P48页)定义顶点的相似;如果属性不是数值性,可以把其转变为数值型进行计算。
A*算法[Hart et al 1968]:
输入:
G1(V1 ,E1,μ1\mu_{1}μ1,ξ1\xi_{1}ξ1) G2(V2,E2,μ2\mu_{2}μ2,ξ2\xi_{2}ξ2)
输出:
pmin={u1−>v3,u2−>ϵ,.......,ϵ−>v6}p_{min}=\{u_{1}->v_{3},u_{2}->{\epsilon },.......,{\epsilon}->{v_{6}}\}pmin={u1−>v3,u2−>ϵ,.......,ϵ−>v6}返回的是将G1通过编辑路径转变为G2的最佳路径,集合里面存放的是编辑操作
初始化集合OPEN为空集合,先存放有待考察的编辑操作P。在A*路径搜索算法中,构造一棵树,树的第0层为空节点,第一层节点表示图G1中一个顶点映射到G2中任何顶点的编辑操作(包括空操作),比如替换、删除操作等。符号化记录为OPEN={u1−>w}OPEN=\{u_{1}->w\}OPEN={u1−>w}其中w表示G2中的顶点或者空点;算法目的是从OPEN中选择cost§最小的节点(一个操作)到集合P_{min}.而考察P是否最小的关键在于使用cost(p)=g(p)+h(p)cost(p) = g(p) +h(p)cost(p)=g(p)+h(p)进行评估。g(p)g(p)g(p)表示从根(空节点)到当前节点(节点中表示操作)的实际代价,h(p)h(p)h(p)表示从当前节点到目标节点的启发式估计(下面补充)。
循环开始:
从OPEN集合中选取代价最小的操作到P_{min}
如果最小操作集合P_{min}中已经有了从G1到G2的完整路径,
那么算法结束返回P_{min}
否则
令P_{min}中存放继续存放最小的编辑操作
若编辑操作数量小于G1中顶点数量
将下一个顶点(u_{k+1}->w)的编辑操作(包括删除)插入到OPEN中,
w表示G2中未处理的顶点
否则
OPEN集合中增加插入操作 $(空顶点 ->w)$
循环结束
补充:
A*算法中的节点p(表示一个编辑操作,也可以用映射符号fff表示)的启发式估计h^\hat{h}h^必须比实际的要小。计算启发式估计的方法如下:
1 计算图G1和G2中未处理的顶点个数n1,n2n_{1},n_{2}n1,n2。选择未处理的顶点个数中较小的个数作为代价矩阵的维度,这个代价矩阵是方阵。构建代价矩阵的目的是为了进行最佳分配,节点的最佳分配的代价记为assignsassign_{s}assigns
2 对于未在方阵中的顶点(比如应该构建(2,3)维度矩阵,但是为了构建方阵删除了其中一列)则这一列的代价记为max(0,n1−n2)max(0,n_{1}-n_{2})max(0,n1−n2),否则记录为max(0,n2−n1)max(0,n_{2}-n_{1})max(0,n2−n1)
因此启发式估计代价就是上面两种成本的加和。





 本文介绍了一系列图数据库实验,包括MUTA、PAH、CMU-HOUSE等数据库的特性及应用,探讨了不同图数据库的密度、顶点属性、边属性及代价函数,对比了密集图与非密集图的区别。
本文介绍了一系列图数据库实验,包括MUTA、PAH、CMU-HOUSE等数据库的特性及应用,探讨了不同图数据库的密度、顶点属性、边属性及代价函数,对比了密集图与非密集图的区别。
















 1033
1033

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








