计算机离散数学及其应用

摘要

本文档适用于计算机专业，
离散数学及其应用附带答案，
70道选择题，50道判断题.30道简答题，20道论述题。

70道选择题

1.设V=<I,+>，令f:I→I,f(x)=x+5， g:I→I,g(x)=8x，h:I→I,h(x)=-x，说法正确的是（ ）。

A、f和g都是V上的自同态映射
B、g和h都是V上的自同态映射
C、只有f是V上的自同态映射
D、f、g和h都是V上的自同态映射
参考答案 B

2.命题a）：如果天下雨，我不去。写出命题a）的逆换式 。

A、如果我不去，天下雨。
B、如果我去，天下雨。
C、如果天下雨，我去。
D、如果天不下雨，我去。
参考答案 A

3.(P→Q)→R的合取范式为（ ） 。

A、(┐P∨R)∧(Q∨┐R)
B、(P∨R)∧(┐Q∨R)
C、P∧Q∧R
D、P∨Q∨R
参考答案 B

4.假设A={a,b,c,d},考虑子集S={{a,b},{b,c},{d}}，则下列选项正确的是（ ）。

A、S是A的覆盖
B、S是A的划分
C、S既不是划分也不是覆盖
D、全部选项都不正确
参考答案 A

5.一棵有向树，如果恰有一个节点的入度为０，其余所有节点的入度都为１，则称为（ ）。

A、根树
B、普通树
C、树根
D、树节点
参考答案 A

6.设< A,+,?? >是一个环，且< B,⊕,⊙>是关于同态映射f的同态象，则< B,⊕,⊙>必定是（ ）。

A、环
B、整环
C、含幺环
D、交换环
参考答案 A

7.*k是Nk={1,2,?,k-1}的模k乘法，则当k=( )时，<Nk,*k>是群。

A、19
B、20
C、21
D、22
参考答案 A

8.对一阶逻辑公式?x?y(P(x,y)∧Q(y,z)∧?xP(x,y))的说法正确的是（ ）。

A、x是约束的，y是约束的，z是自由的；
B、x是约束的，y既是约束的又是自由的，z是自由的；
C、x是约束的，y既是约束的又是自由的，z是约束的；
D、x是约束的，y是约束的，z是约束的；
参考答案 B

9.设无向图中有6条边，3度与5度顶点各1个，其余顶点都是2度点，问该图有多少个顶点？（ ）

A、
5
B、
4
C、
2
D、
6
参考答案 B

10.设有向图（a）、（b）、（c）、（d）如下图所示，则下列结论成的是（）

11.令S={a，b}，S上有4个二元运算

12.下列推理步骤错在（）

(1)?x(F(x)→G(x)) P
(2) F(y)→G(y) US(1)
(3) ?xF(x) P
(4) F(y) ES(3)
(5) G(y) T(2)(4)I
(6) ?xG(x) EG(5)
A、(2)
B、(4)
C、(5)
D、(6)
参考答案 B

13.设h是群G上的一个同态，|G|=12，|h(G)|=3，则|K|（K是h的核）=（ ）。

A、1
B、2
C、3
D、4
参考答案 D

14.对于公式?x（??yP(x,y)→(?zQ(z)→R(x)的前束范式，下列各式中，哪式是正确的（）。

A、?x?y?z（P(x,y)∨?Q(z)∨R(x))
B、?x?y?z（P(x,y)∨?Q(z)∨R(x))
C、?x?y?z（P(x,y)∨Q(z)∨R(x))
D、?x?y?z（P(x)∨?Q(z)∨R(x))
参考答案 A

15.是命题的是（ ）。

A、x大于y
B、d是整数
C、他昨天做了十五道题
D、a是大学生
参考答案 C

16.设< , >是正实数乘法群，<R,+>是实数加法群。令f： f(x) ，则（ ）

17.不是命题的是（ ）。

A、5大于3
B、11是质数
C、他是优秀学生
D、k是太阳
参考答案 D

18.公式 为仅含有逻辑联结词┐，∧，∨及命题变元P1 ，，…，Pn 的命题公式， A*是A的对偶式，则 (┐ P1,┐P2 ，…，┐ Pn)=> ( )。

19.下面哪一个是?x(P(x)→(?y)((?z)Q(x,y)→?(?z)R(x,y)))的前束合取范式（）。

A、?x?y(P(x)??Q(x,y)??R(x,y,u))
B、?x?y(?P(x)?Q(x,y)??R(x,y,u))
C、?x?y(?P(x)??Q(x,y)?R(x,y,u))
D、?x?y(?P(x)??Q(x,y)??R(x,y,u))
参考答案 D

20.设<G,>是n阶有限群，如果n为（ ），则<G,>必是循环群。

A、奇数
B、偶数
C、质数
D、合数
参考答案 C

21.n 个节点的无向完全图Kn的边数为( )。

23.无向简单图G是棵树，当且仅当（）

A、
G连通且边数比结点数少1
B、
G连通且结点数比边数少1
C、
G的边数比结点数少1
D、
G中没有回路
参考答案 A

24.只有你走，我才留下。设P: 你走。 Q：我留下。则命题符号化为（ ） 。

A、
┐Q∧┐P
B、
Q→P
C、
P→Q
D、
Q?P
参考答案 B

25.设L(x)：x是演员，J(x)：x是老师，A(x,y)：x佩服y。那么命题“所有演员都佩服某些老师”符号化为( )

A、
?xL(x)→A(x,y)
B、
?x(L(x)→?y (J(y)?A(x,y) ))
C、
?x?y(L(x)?J(y)?A(x,y))
D、
?x?y(L(x)?J(y)→A(x,y))
参考答案 B

26.P：今天下雨。 Q：明天下雨。上述命题的合取为（ ） 。（符号表示）

A、
┐P∧┐Q
B、
┐P∨Q
C、
┐P∨┐Q
D、
P∧Q
参考答案 D

27.设G是连通(n,m)的平面图，有r个面，且每个面的次数至少为L( L≥3 )，则（ ）。

A、
m≥3n-6
B、

C、
m+n-r=2
D、
m+r-n=2
参考答案 B

28.设R(x)：x是实数，Q(x)：x是有理数。命题“并非每个实数都是有理数”可符号化为（ ）。

A、
?(?x)(R(x)→Q(x)
B、
?(?x)(R(x)→?Q(x)
C、
?(?x)(R(x)→Q(x)
D、
?(?x)(R(x)?Q(x)
参考答案 A

29.图G所示平面图deg(R3)为( )。

A、
4
B、
5
C、
6
D、
3
参考答案 B

30.从 {0,2}到{a，b，c，d}的二元关系R：{<<0,0>,a>,<<0,1>,b>,<<1,0>,c>,<<1,1>,b>}是( )函数。

31.设有向图D为欧拉图，则图D中每个结点的入度（ ）出度。

A、
等于
B、
大于
C、
小于
D、
不能确定
参考答案 A

32.没有不犯错误的人。M(x)：x为人。F（x）：x犯错误。则命题可表示为（ ）。

A、
(?x)(M(x)→F(x)
B、
(?x)(M(x)?F(x)
C、
（?x）(M(x)?F(x))
D、
(?x)(M(x)→F(x)
参考答案 A

33.（1）燕子北回，春天来了。设P: 燕子北回。 Q：春天来了。则（1）可以表示为（ ） 。

A、
P→Q

B、
Q→P

C、
P?Q

D、
P ∨Q

参考答案 C

34.群<R, >与<R-{0}, >之间的关系是（ ）。

A、
同态
B、
同构
C、
后者是前者的子群
D、
B、C均正确
参考答案 A

35.命题公式(P→Q∧┐P)的类型是（ ）。

A、
重言式

B、
矛盾式

C、
可满足式

D、
永真式

参考答案 C

36.函数f：R×R→R，f(x,y)=（x+y）/2是( )函数。

A、
入射

B、
满射

C、
双射

D、
以上答案都不对

参考答案 B

37.设完全图Kn有n个结点（n>2），m条边，当（ ）时，Kn中存在欧拉回路。

A、
m为奇数
B、
n为偶数
C、
n为奇数
D、
m为偶数
参考答案 C

38.设G 为至少有三个结点的连通平面图，则G 中必有一个结点u，使得（ ）。

A、
deg(u)<5
B、
deg(u)=5
C、
deg(u)>5
D、
deg(u)≤5
参考答案 D

39.下列关系中哪些能构成函数？（ ）

A、
{〈x,y〉|x,y∈ N,x+y<10}
B、
{〈x,y〉|x,y∈ N,x+y=10}
C、
{〈x,y〉|x,y∈ R,|x|=y}
D、
{〈x,y〉|x,y∈ R,x=|y|}
参考答案 C

40.对于公式?x?y((?zP(x,y,z)∧?uQ(x,u)→?vQ(y,v)的前束范式，下列各式中，哪式是正确的？（ ）

A、
?x?y?z?u?v(?P(x,y,z)∨?Q(x,u)∨Q(y,v)
B、
?x?y?z?u?v(?P(x,y,z)∨?Q(x,u)∨Q(y,v)
C、
?x?y?z?u?v?P(x,y,z)∨?Q(x,u)∨Q(y,v)
D、
?x?y?z?u?v(?P(x,y,z)∨?Q(x,u)∨Q(y,v)
参考答案 D

41.设个体域是整数集合， 下面描述正确的是（ ）。

A、
P是一阶谓词公式，但不是命题
B、
P是假命题
C、
P是真命题
D、
P不是一阶谓词公式
参考答案 A

42.谓词公式F(x,y,z)→?x?yG(x,y,z)中的变元x（ ）。

A、
是自由变元但不是约束变元
B、
既不是自由变元又不是约束变元
C、
既是自由变元又是约束变元
D、
是约束变元但不是自由变元
参考答案 C

43.设G为Mn®上的加法群，n≥2，下列哪个子集不能构成G的子群。（ ）

A、
全体对称矩阵
B、
全体对角矩阵
C、
全体行列式大于等于0的矩阵
D、
全体上（下）三角矩阵
参考答案 C

44.设G=是24阶的循环群，则G共有（ ）个生成元。

A、
4
B、
6
C、
8
D、
10
参考答案 A

45.关于半群的性质，下面说法不正确的是（ ）。

A、
若<S,>是一个半群，B?S 且在B上是封闭的，那么<B,*>也是一个半群。

B、
若<S, * >是一个半群，如果S是一个有限集，则必有a∈S,使得a * a=a。

C、
若? 表示普通的乘法运算，那么<[0,1],?>、< [0,1) ,?>和<I,?>都是<R,?>的子半群

D、

参考答案 D

46.设〈G , *〉是一个独异点，并且对于G中的每一个元素a都有（ ），则〈G , * 〉是一个阿贝尔群。

A、
a * a= a
B、
a * a= e
C、
a * e= e
D、
e* a= e
参考答案 B

47.设集合 A={1,{2},a,4,3}，下面命题为真是 （ ）。

A、
2∈A
B、
1∈A
C、
5∈A
D、
{2}
参考答案 B

48.张三或李四都可以做这件事。设P：张三可以做这件事。Q：李四可以做这件事。则命题符号化为（ ） 。

A、
┐P∧┐Q
B、
┐P∨Q
C、
┐P∨┐Q
D、
P∧Q
参考答案 D

49.设是代数系统，+和是普通数的加法和乘法。当X=（ ）时，是整环。

A、
{x│x=2n,n∈I}

B、
{x│x=2n+1,n∈I}

C、
{x│x≥0,x∈I}

D、
{x│x=a+b√3,a,b∈R}

参考答案 D

50.在一个具有n个节点的图中，则任何简单路的长度均不大于（ ）。

A、
n
B、
n-1
C、
n+1
D、
2n
参考答案 B

51.设A、B两个集合，当（ ）时A-B=B。

A、
A=B
B、
A?B
C、
B?A
D、
A=B=?
参考答案 D

52.设U={1，2，3，4，5}，A={2，4}，B={4，3，5}，C={2，5，3}，确定集合(A-C)-B = （ ）。

A、
{1,4}

B、
{2,3,4,5}

C、
{4}

D、
?

参考答案 D

53.设G是有6个结点的完全图，从G中删去（ ）条边，则得到树。

A、
6
B、
9
C、
10
D、
15
参考答案 C

54.下列命题公式与A→B等价的是( ) 。

A、
A→┐B
B、
┐B∧A

C、
┐A∨B

D、
B∧A

参考答案 C

55.设图G是汉密尔顿图，则G一定是（ ）。

A、
欧拉图
B、
树
C、
多重图
D、
连通图
参考答案 D

56.A={2,4,6,8}上的二元运算定义为：ab=max{a,b}，则在代数系统中，幺元和零元分别是（ ）。

A、
2和8
B、
4和6
C、
6和8
D、
8和2
参考答案 A

57.S(a)?W(a)可以表示什么意思？（ ）

A、
小明的学习很好，但是体育不好
B、
小明工作好，小花学习好
C、
小明工作和学习都好
D、
小明和小花都很高
参考答案 C

58.欧拉公式的原型为（ ）。

A、
v+e+r＝2
B、
v-e+r＝2
C、
v-e-r＝2
D、
v+e-r＝2
参考答案 B

59.下面关于广群，半群，独异点，群的关系正确的是（ ）。

A、
{群}{独异点} {半群} {广群}

B、
{广群}{半群} {独异点} {群}

C、
{半群}{独异点} {群} {广群}

D、
{群}{半群} {独异点} {广群}

参考答案 A

60.下图的最小生成树的权为（ ）。

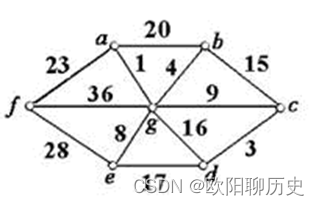
A、
40
B、
44
C、
48
D、
52
参考答案 C

61.设G是有n个结点，m条边的连通图，必须删去G的( )条边，才能确定G的一棵生成树．

A、
m-n+1
B、
m-n
C、
m+n+1
D、
n-m+1
参考答案 A

62.联结词↑可以转化为由┐和∧表示，P↑Q?（ ） 。

A、
┐P∧┐Q

B、
┐P∧Q

C、
┐(P∧Q)

D、
┐P∨Q

参考答案 C

63.下图的最小生成树是（ ）。

A、

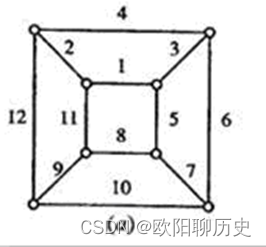
B、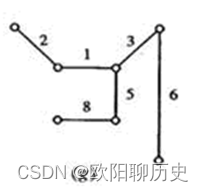

C、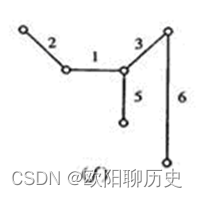

D、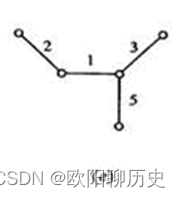

参考答案 D

64.下列表达式正确的有（ ）。

A、
?(P→Q)=>Q
B、
P?Q=>P
C、
(P?Q)?(P??Q)<=>P
D、
P→(P→Q)<=>T
参考答案 C

65.设< X,+, × >是代数系统，+和是普通加法和乘法，当X=（ ），< X,+, × >是域。

A、
{x│x≥0,x∈I}

B、
{x│x=a+b√3,a,b∈Q}

C、
{x│x=a+b?5,a,b∈Q}

D、
{x│x=a/ b,a,b∈N,a≠kb}

参考答案 B

66.给定序列集合｛000，001，01，10，0｝，若去掉其中的元素（ ），则该序列集合构成前缀码。

A、
000

B、
001

C、
01

D、
0
参考答案 D

67.在代数系统中，整环和域的关系为( )。

A、
整环一定是域
B、
域不一定是整环
C、
域一定是整环
D、
域一定不是整环
参考答案 C

68.给定一命题公式，若无论对分量做怎样的指派，其对应的真值永为T，则称该命题公式为（ ） 。

A、
重言式
B、
永假式
C、
可满足式
D、
矛盾式
参考答案 A

69.对偶式为P↑Q表达式是（ ） 。

A、
P∧Q

B、
P↓Q

C、
P∨Q

D、
P→Q

参考答案 B

70.设G是有n个结点，m条边的连通图，必须删去G的（ ）条边，才能确定G的一棵生成树。

A、
m-n+1
B、
n-m
C、
m+n+1
D、
n-m+1
参考答案 A

50道判断题

1.补交转换律的公式为A-B = A∩~B。

正确
错误
参考答案 正确

2.一般情况下，笛卡尔积不满足交换律和结合律。（ ）

正确
错误
参考答案 正确

3.设Z为整数集，? a,b∈Z,a°b=a+b-1,? a,b∈Z,a 的逆元a-1是2-a

正确
错误
参考答案 正确

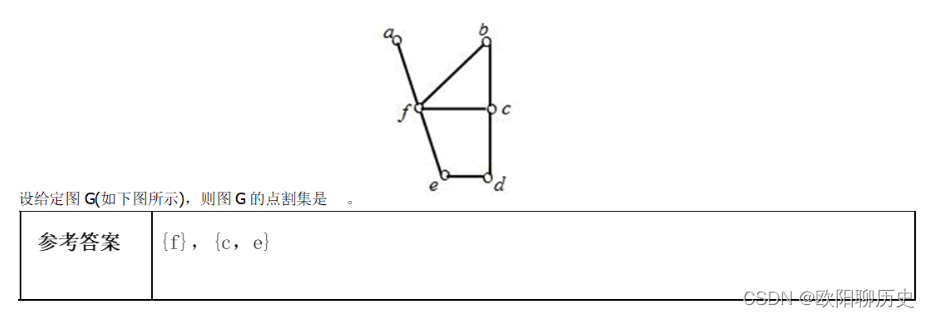
4.给定的图G，则图G的点割集｛f｝，｛c，e｝。

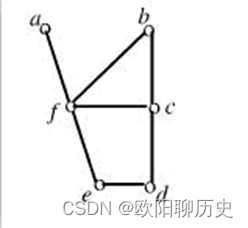
正确
错误
参考答案 正确

5.粗线描绘出的是下图的最小生成树。

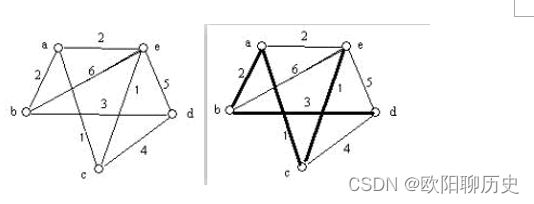
正确
错误
参考答案 错误

6.由公式的等价性知：C1∧C2∧…∧Cn→(A→B)? C1∧C2∧…∧Cn∧(A→B)。

正确
错误
参考答案 正确

7.N为自然数集，N上的运算定义为：xy=min{x,y}，其中x,y∈N，则<N,*>是独异点。

正确
错误
参考答案 正确

8.设<A,+.*>是一个代数系统，如果满足：

(1)<A,+>是阿贝尔群;
(2)<A,>是可交换独异点;
(3)运算?对于运算+是可分配的。
则称<A,+.>是域。
正确
错误
参考答案 错误

9.设P、Q为两个命题公式，若P↑Q的真值为F，则P为T且Q为T。

正确
错误
参考答案 正确

10.可满足式一定是重言式。（ ）

正确
错误
参考答案 错误

11.设G是平面图。将G嵌入平面后，由G的边将所在的平面划分为若干个区域，每个区域称为G的一个面。

正确
错误
参考答案 正确

12.可达性矩阵用来表明了图中任意两个结点间是否至少存在一条路以及在任何结点上是否存在回路。

正确
错误
参考答案 正确

13.最优二叉树是唯一的。

正确
错误
参考答案 错误

14.设G是一个联结词的集合，若任意一个命题公式都可用G中联结词构成的公式来表示，则称G为最小联结词组。

正确
错误
参考答案 错误

15.下图是汉密尔顿图。（ ）

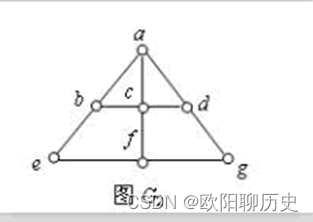
正确
错误
参考答案 正确

16.对于存在指定规则，其指定的客体c是任意的。

正确
错误
参考答案 错误

17.在一阶谓词公式中，同一变元符号不能够既约束出现又自由出现。

正确
错误
参考答案 错误

18.任何一棵二叉树的树叶可对应一个前缀码。 （ ）

正确
错误
参考答案 正确

19.若公式F的主合取范式是一空公式且为1，则F是永假公式。

正确
错误
参考答案 错误

20.两个具有固定次序的客体组成一个有序序列，称为序偶，简记为<a,b>，它常常表达两个客体之间的关系。

正确
错误
参考答案 正确

21.一个连通平面图的对偶图也必是平面图。

正确
错误
参考答案 正确

22.设集合,B={a,b,{c}},判断{?}?B是否正确。

正确
错误
参考答案 错误

23.循环群一定是阿贝尔群，阿贝尔群也一定是循环群。

正确
错误
参考答案 错误

24.设Z为整数集合，在Z上定义二元运算*：? x,y∈Z,xy=x+y-2，则<Z,>是群。

正确
错误
参考答案 正确

25.今天天气真好啊！这句话是个命题。

正确
错误
参考答案 错误

26.设〈G，〉是一个循环群， a是其生成元。若|G|＝m， 则〈G，〉与〈Zm, +m〉同构。

正确
错误
参考答案 正确

27.如果P?Q，那么P?Q。

正确
错误
参考答案 错误

28.在真值表中，对于每一个H1, H2,…, Hm真值均为T的行，若C也有真值T，则H1∧H2∧…∧Hm ? C成立。 （ ）

正确
错误
参考答案 正确

29.下图存在一条欧拉回路。（ ）

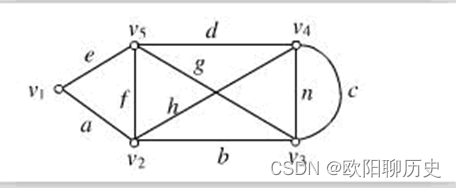
正确
错误
参考答案 正确

30.下列句子是一个命题：是大学生。

正确
错误
参考答案 错误

31.设n∈Z,n≥2,则n阶实矩阵的集合Mn®关于矩阵加法和乘法构成环，它是含幺环，交换环，也是无零因子环。（ ）

正确
错误
参考答案 错误

32.若A?B，则B?┐A。 （ ）

正确
错误
参考答案 错误

33.设△和δ是简单图G的最大度和最小度，则δ≤2m / n≤△。（ ）

正确
错误
参考答案 正确

34.若2大于3.则2大于4。S(x,y)：x大于y。a：2，b：3。c ：4。于是命题的谓词表达式可以为：S（a,b）。

正确
错误
参考答案 错误

35.一个图是平面图，当且仅当它不包含与K3,3或K5在2度结点内同构的子图。这是Kuratowski库拉托夫斯基定理。

正确
错误
参考答案 正确

36.数理逻辑的主要任务是提供一套推理规则。 （ ）

正确
错误
参考答案 正确

37.公式?xP(x)→?yQ(x,y)的前束范式是?x?y(P(x)→Q(x,y)。（ ）

正确
错误
参考答案 错误

38.设A是一个集合,如果A上的一个关系R,满足自反性、对称性、传递性，则称R是A上的一个偏序关系，并把它记做 “≤” ；如果集合A上有偏序关系≤ ，则称A为偏序集，用序偶<A，≤>表示之。 （ ）

正确
错误
参考答案 正确

39.设A = { a+bi | a ,b∈Q }, 其中i2= -1, 运算为复数加法(+)和乘法(*).则是整环。（ ）

正确
错误
参考答案 正确

40.若命题P为真，则?P为假。

正确
错误
参考答案 正确

41.若公式中有n个命题变元，则按二进制从小到大的顺序共有2n种赋值。

正确
错误
参考答案 正确

42.下图中（c）和（d）是根树。 （ ）

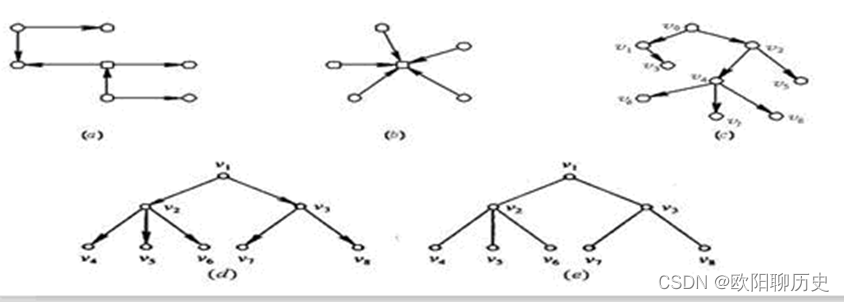
正确
错误
参考答案 正确

43.┐(P∧Q)不是命题公式。 （ ）

正确
错误
参考答案 错误

44.陈述句“x+y>4”是个命题。

正确
错误
参考答案 错误

45.四个顶点的非同构简单图有11个 。（ ）

正确
错误
参考答案 正确

46.连通图至少有一棵生成树。 （ ）

正确
错误
参考答案 正确

47.若 为一个群，<H,>和<K,>都是群<G,>的子群，则<H∩K，>也是<G,*>的子群。

正确
错误
参考答案 正确

48.设代数系统V=?{a,b},?是半群，且aa=b,则ab=ba。 ( )

正确
错误
参考答案 正确

49.设G为非零有理数乘法群，H={1,-1}，则H的左陪集是：? a∈Q+，aH={a,-a}，其中Q+是正有理数集。

正确
错误
参考答案 正确

50.“中国人民是伟大的。"是一个命题。 （ ）

正确
错误
参考答案 正确

30道填空题

1.设给定图G(如下图所示)，则图G的点割集是 。

2.P：你努力，Q：你失败。“除非你努力，否则你将失败”的翻译为_____________。

3.设< {a,b,c}, * >为代数系统，* 运算如下：

4.设<R，+，·>是代数系统，如果①<R，+>是交换群 ②<R，·>是半群 ③_____________，则称<R，+，·>为环。 参考答案 ·对+可分配

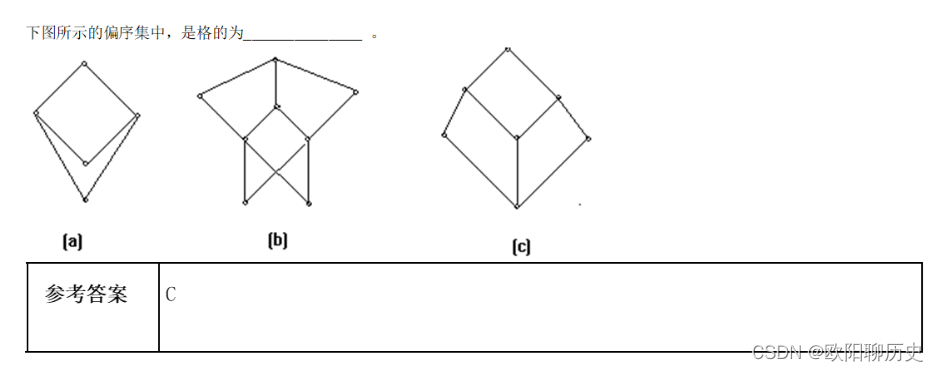
5.下图所示的偏序集中，是格的为______________ 。

6.若解释I的论域D仅包含一个元素，则

7.设<G,*>是非零实数乘法群，f:G→G是同态映射，f(x)=1/x，则f(G)=_，Ker(f)=。

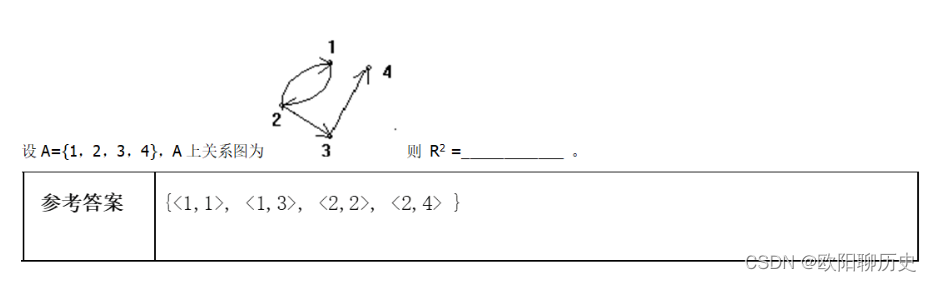
8.设A={1，2，3，4}，A上关系图为 则 R2 =____________ 。

9.A，B，C表示三个集合，文图中阴影部分的集合表达式为____________________。

11.在一阶谓词逻辑中，将命题“没有不能表示成分数的有理数”符号化为________(设F(x):x是有理数；G(x):x能表示成分数。)

参考答案 ??x(F(x)∧?G(x))或?x(F(x)→G(x))

12.设A是素数集合，B是奇数集合，则A-B=__________。

参考答案 {2}

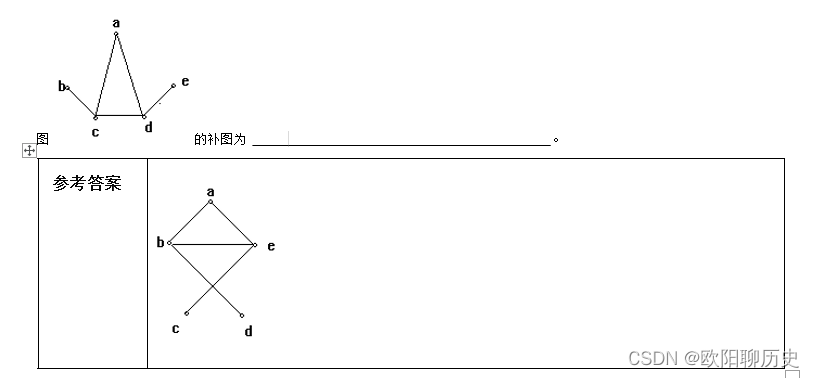
13.图 的补图为

14.设<S,>是一个代数系统，其中S={a,b,c}，的定义如表5-1所示，则<S,>_______半群，<S,>______独异点。

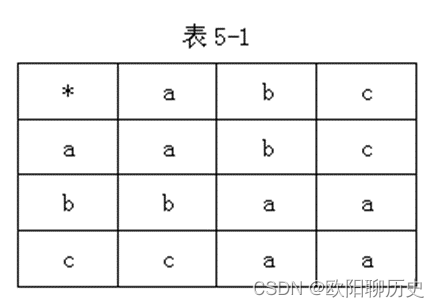
参考答案 不是；不是

15.论域D={1，2}，指定谓词P

16.逻辑学是一门研究________及________的科学。

参考答案 思维形式、思维规律

17.给定一个序列集合{1，01，10，11，001，000}，若去掉其中的元素________，则该序列集合构成前缀码。

参考答案 1

18.设S={a1 ，a2 ，…，a8}，Bi是S的子集，则由B31所表达的子集是__________________。

19.设代数系统<A，*>，其中A={a，b，c},则具有的性质为_____________________.

20.令[a,b]表示实数的闭区间，即[a,b]={x|a≤x≤b}，f:[0,1]→[a,b]定义为：f(x)=(b-a)x+a，则这个映射是_______映射。

参考答案 双射

21.设X={0,1,2},Y={a,b,c}。若f:X→Y为：f={<0,c>,<1,a>,<2,b>}，则有f-1:Y→X，则f-1=_____________。

参考答案 {<a,1>,<b,2>,<c,0>}

22.有向图 中从v1到v2长度为2的通路有________条。

23.设G为9阶无向图，每个结点度数不是5就是6，则G中至少有__________个5度结点。

参考答案 6

24.用列举法表示下列集合A={x|x∈N且x2≤9}，则可表示为______________。

参考答案 {1,2,3}

25.设|X|=n，|Y|=m，则当n,m满足___________ 时，存在双射，有_______________个不同的双射。

参考答案 n=m、n!

26.设 P（x）：x是素数， E(x)：x 是偶数，O(x)：x是奇数 N (x,y)：x可以整数y。则谓词 的自然语言是（）

27.已知图G中有1个1度结点，2个2度结点，3个3度结点，4个4度结点，则G的边数是________。

参考答案 15

28.设X={a,b,c,d},Y={1,2,3,4,5}，且有f={<a,1>,<b,3>,<c,4>,<d,4>}，则 dom f=,Rf=___ .

参考答案 {a,b,c,d};{1,3,4}

29.设完全图 有n个结点(n2)，m条边，当 （）时， 中存在欧拉回路．

30.设个体域D={1,2}，那么谓词公式?xA(x)∨?yB(y)消去量词后的等值式为（）。

参考答案 A(1)∨A(2)∨(B(1)∧B(2))

30道简答题

1.n为何值时，无向完全图Kn是欧拉图？n为何值时，无向完全图Kn仅存在欧拉道路而不存在欧拉回路？

参考答案 当n为大于2的奇数时，无向完全图Kn是欧拉图，因为每个节点的度数为偶数。当n为2时，K2，是唯一存在两个奇度点的完全图，因此此图只存在欧拉道路。

2.设R为实数集合，对x∈R，有f(x)=x+2, g(x)=x-2 ,h(x)=3x，求g°f, h°g,(h°g)°f与h°(g°f)。

参考答案 g°f={<x,x>|x∈R}
h°g={<x,3(x-2)>│x∈R}
(h°g)°f={<x,3x>│x∈R}
h°(g°f)={<x,3x>|x∈R}
所以有h°(g°f)=(h°g)°f 。

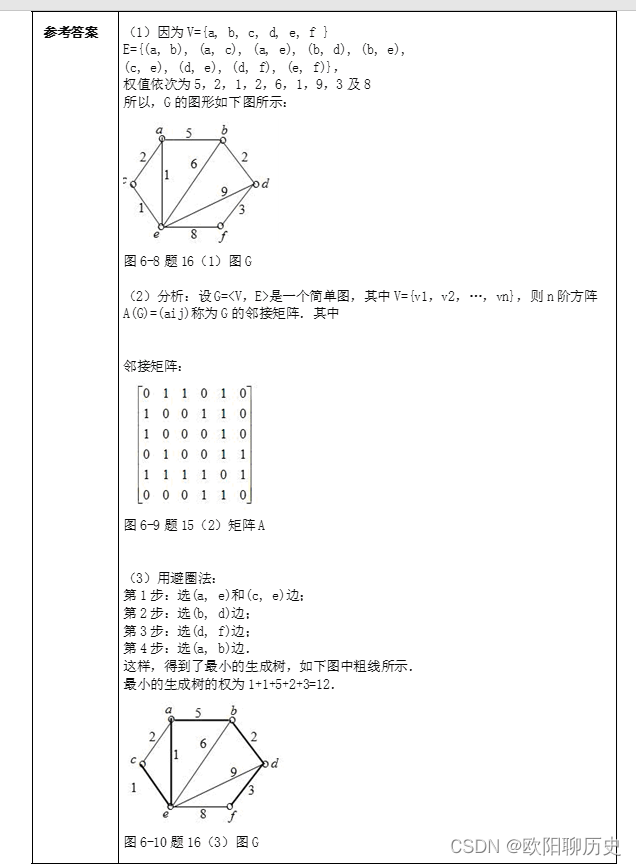
3.图G=<V, E>，其中V={a, b, c, d, e, f }，E={(a, b), (a, c), (a, e), (b, d), (b, e), (c, e), (d, e), (d, f), (e, f)}，对应边的权值依次为5，2，1，2，6，1，9，3及8．

（1）画出G的图形；
（2）写出G的邻接矩阵；
（3）求出G权最小的生成树及其权值．

4.将命题符号化：李强比王飞高。

参考答案 符号化为B(c,d)，其中，c：李强，d：表示王飞，B(x,y)：…比…高”。

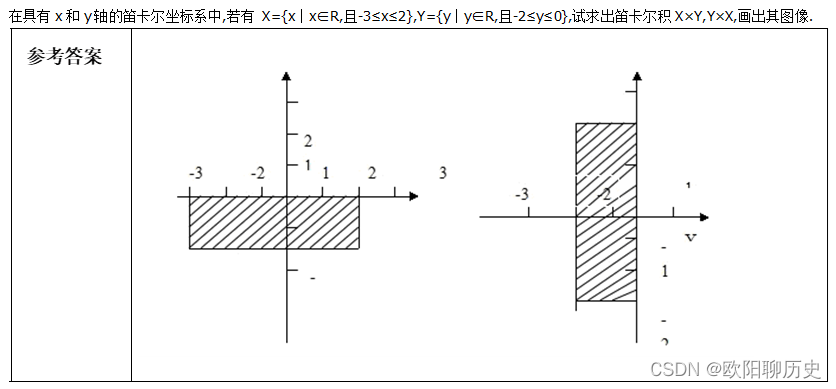
5.在具有x和y轴的笛卡尔坐标系中,若有 X={x︱x∈R,且-3≤x≤2},Y={y︱y∈R,且-2≤y≤0},试求出笛卡尔积X×Y,Y×X,画出其图像.

6.对于正整数k, Nk={0,1,2,?,k-1},设k是Nk上的一个二元运算,使得ak b=(a*b) mod k, a,b∈Nk

a) 当k=4时，试造出*k的运算表
b) 对于任意正整数k,证明?Nk,*k ?是一个半群。

7.设解释R如下：DR是实数集，DR中特定元素a=0，DR中特定函数 ，特定谓词 ，问公式 的涵义如何？真值如何？

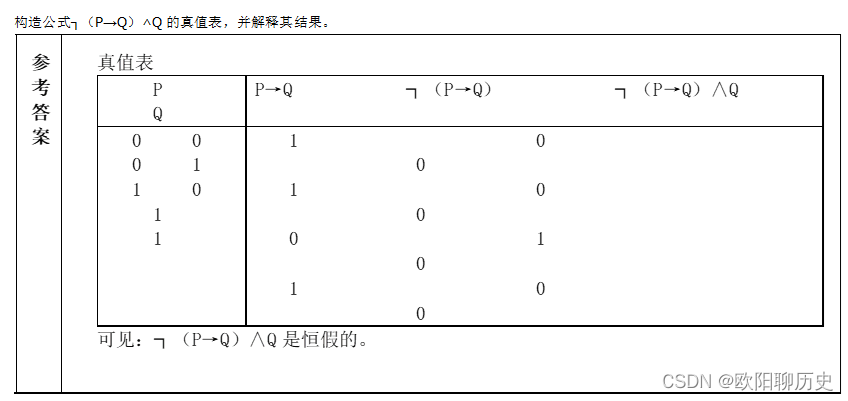
8.构造公式┐（P→Q）∧Q的真值表，并解释其结果。

9.判定以下论断哪些是恒成立的?哪些是恒不成立的?哪些是有时成立的?

(1)若a∈A,则a∈A∪B;
(2)若a∈A,则a∈A∩B;
(3)若a∈A∪B,则a∈A;
(4)若a∈A∩B,则a∈B;
(5)若a A,则a∈A∪B;
(6)若a A,则a∈A∩B;
(7)若A?B，则A∩B=A;
(8)若A?B,则A∩B=B.

参考答案
(1)恒成立.因为A? A∪B,若a∈A,则a∈A∪B.
(2)有时成立.若a∈A,但a?B,则a? A∩B;若a∈A,且a∈B,则a∈A∩B.
(3)有时成立.若a∈A∪B,可能有三种情形: a∈A,但a?B,或者a?A但a?B或者a∈A且a∈B对于第一、三种情形，有a∈A，但是第二种情形，a?A。
（4）恒成立。因为a∈A∩B，必有a∈A，且a∈B。
（5）有时成立。虽然a?A，但是，有a∈B或a?B两种可能，若a?B，则a?A∪B；若a∈B，有a∈A∪B。
（6）恒不成立。因为a?A，即使a∈B，也有a?A∩B，若a?B，更有a?A∩B
（7）恒成立。当A?B，A是B的子集，当然满足A∩B=A。
（8) 有时成立。既然A?B，就有两种可能：A=B或者A?B。若A=B，则A∩B=B成立；若A?B，则A∩B=B就不成立。

10.求等价于下面wff的前束合取范式与前束析取范式：?xP(x)??xQ(x)→(?x)(P(x)?Q(x)。

参考答案 因为 ，所以为永真式，不写为前束范式的形式。

11.设f,g均为实函数，f(x)=2x+1 ,g(x)=x2+1。求f°g, g°f,f°f,g°g。

12.S=Q×Q，Q为有理数集，为S上的二元运算，? ?a,b?,?x,y?∈S有 ?a,b?* ?x,y?=?ax,ay+b?。 问 * 运算是否有幺元、零元？如果有，请指出，并求S中所有可逆元素的逆元。

参考答案 容易验证?1,0?为幺元，没有零元。当a≠0时，?a,b?的逆元为?1/a,b/a?

13.对于给定的 f 和集合A，请判断 f 性质(类型)；并求A在 f 下的像f(A)。

(1) f∶ R→ R ，f(x)=x，A={8}
(2) f∶ N→N×N，f(x)=〈x,x+1〉，A={2,5}
(3) f∶ Z→N，f(x)=|x|，A={-1,2}
(4) f : S→ R ，f(x)=1/(x+1) ,S=［0,+∞)，A=［0,7)
(5) f∶ [0,1]→[a,b],a ≠b,f (x)=(b-a) x +a,A=[0,1/2)

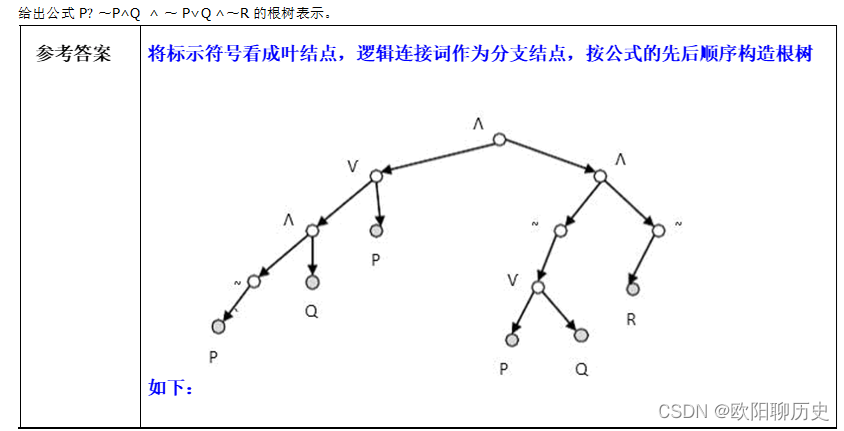
14.给出公式 P? ～P∧Q ∧ ～ P∨Q ∧～R 的根树表示。

15.设R1和R2是非空集合A上的等价关系，下列各式哪些是A上的等价关系？哪些不是A上的等价关系？

16.设集合A={1,2,3,4}，A上的关系R，求出它的自反闭包、对称闭包和传递闭包。

参考答案

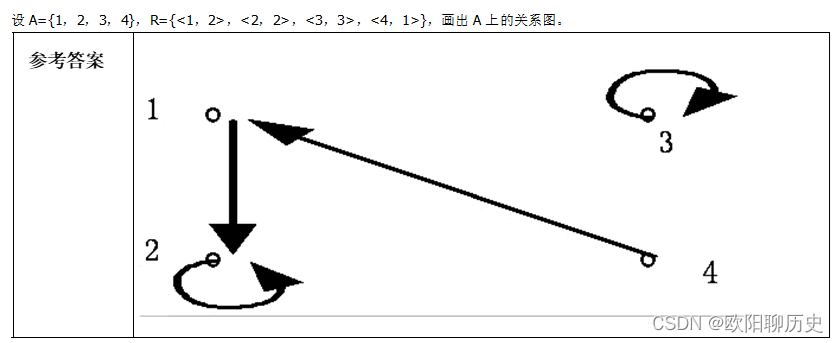
17.画出A上的关系图。

18.设X求和 。

19.集合A={1,2,3,4}，A上的关系R的关系矩阵为

20. 试给出G的图形表示；

求G的邻接矩阵；

判断图G是强连通图、单侧连通图还是弱连通图？

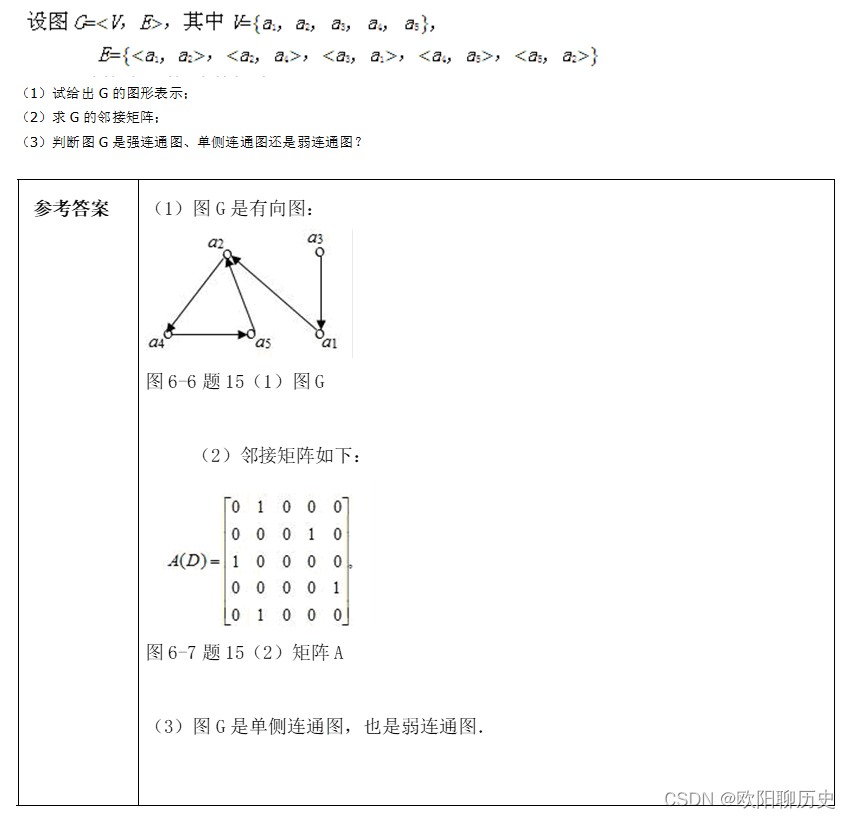
21.设G={[1],[2],[3],[4],[5],[6]}，G上的二元运算×7如表所示。

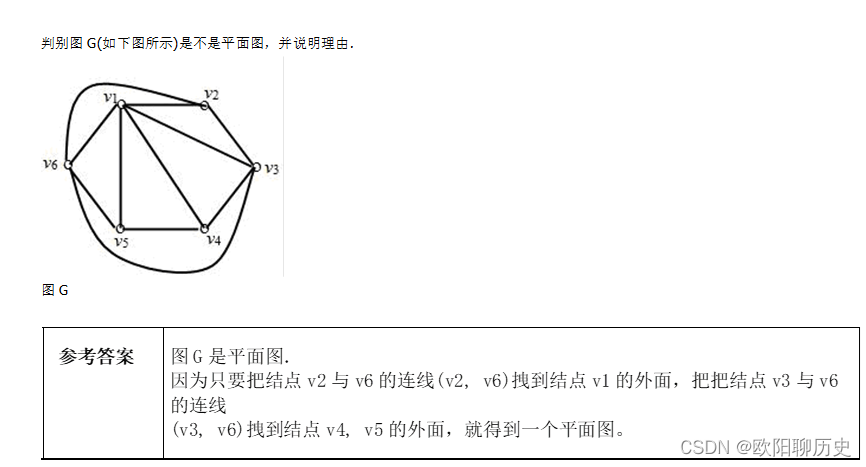
22.判别图G(如下图所示)是不是平面图，并说明理由．

23.试将公式化成等价的前束范式：?xF(x)→?xQ(x)。

参考答案 ?xF(x)→?xQ(x)=??xF(x)∨?xQ(x)=?x?F(x)∨?xQ(x)=?x(?F(x)∨Q(x))

24.给定两个图G1，G2（如下图所示）

（1）试判断它们是否为欧拉图、汉密尔顿图？并说明理由。
（2）若是欧拉图，请写出一条欧拉回路。

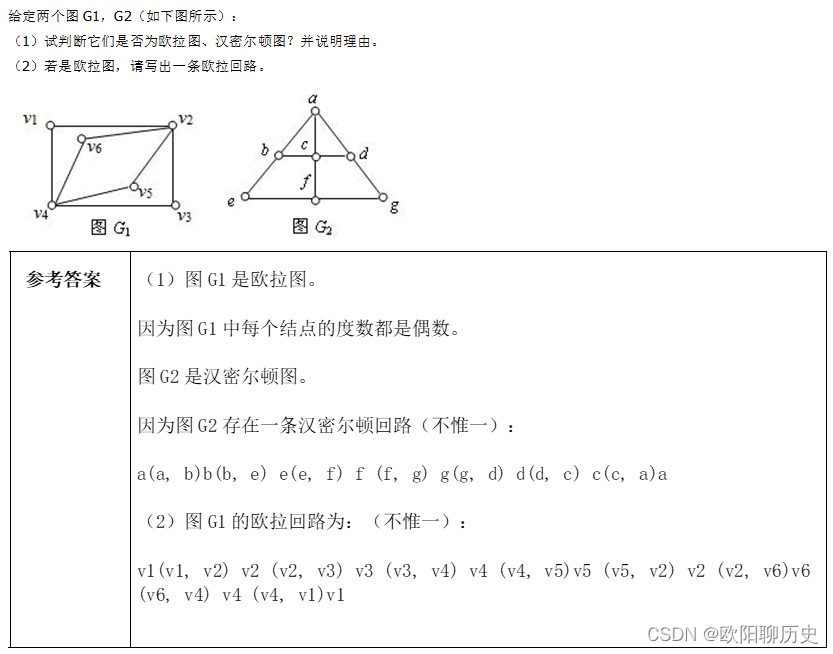
25.求等价于下面wff D的前束合取范式与前束析取范式。

26.设集合A={1,2,3,4}，A上的四个偏序关系分别为

试分别画出它们的哈斯图，并判断起其中哪个具有全序关系？哪个具有良序关系？

27.设R为实数集合

对x∈R，有f(x)=x+2, g(x)=x-2 , h(x)=3x，求g°f , h°g, (h°g)°f与h°(g°f)
参考答案 解：
g°f={<x,x>|x∈R}
h°g={<x,3(x-2)>│x∈R}
(h°g)°f={<x,3x>│x∈R}
h°(g°f)={<x,3x>|x∈R}
所以有h°(g°f)=(h°g)°f

28.下列集合中，哪些是映射？并求映射的定义域和值域。

（1）S1={<1,<2,3?,<2,❤️,4?,❤️,<1,4?,<4,<1,4?}
（2）S2={<1,<2,3?,<2,❤️,4?,❤️,❤️,2?}
（3）S3={<1,<2,3?,<1,<2,4?,<2,❤️,4?
（4）S4={<1,<2,3?,<2,<2,3?,❤️,<2,3?
参考答案 （1）是映射。domS1={1,2,3,4}，RS1={<1,4>,<2,3>,❤️,4>}
（2）是映射。domS2={1,2,3}，，RS2={<2,3>,❤️,2>,❤️,4>}
（3）不是映射。
（4）是映射。domS4={1,2,3}，RS4={<2,3>}

29.设R的关系图如下图所示，试画出r®,s®和t®的关系图。

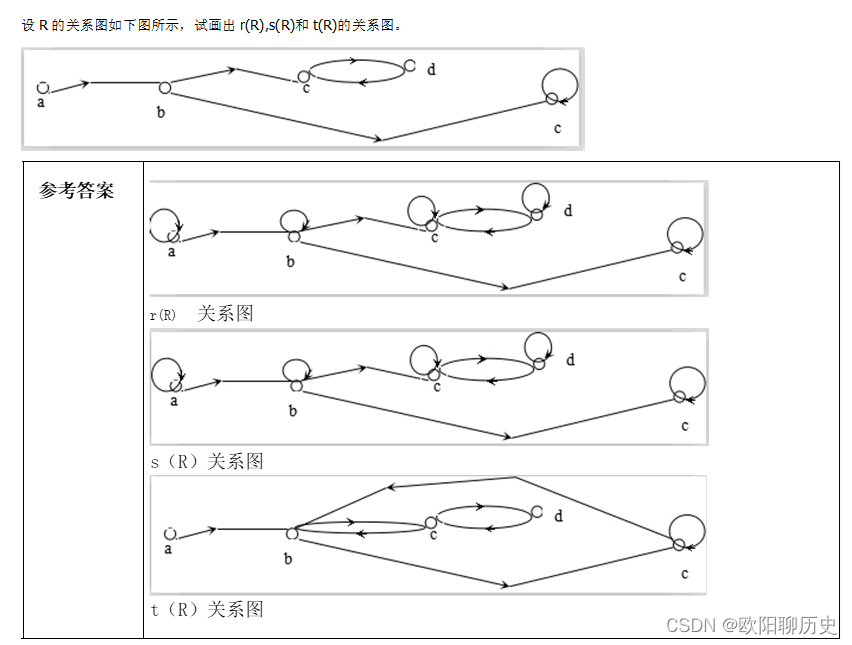
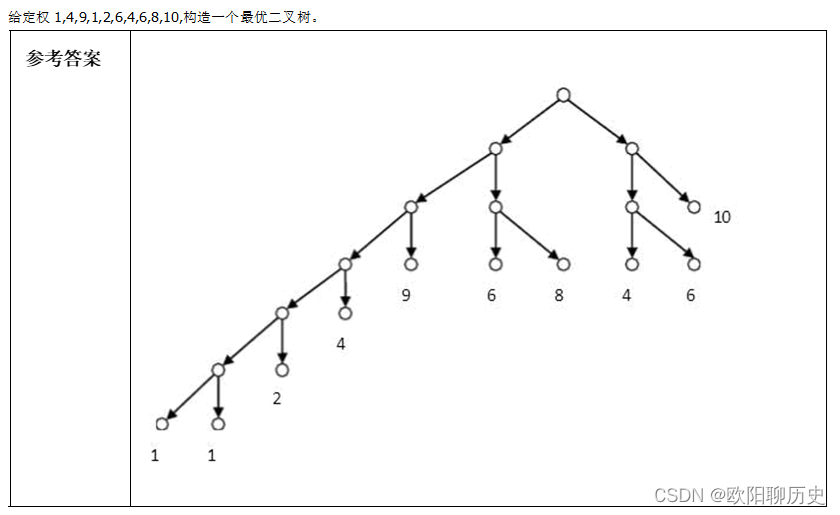
30.给定权1,4,9,1,2,6,4,6,8,10,构造一个最优二叉树。

20道论述题

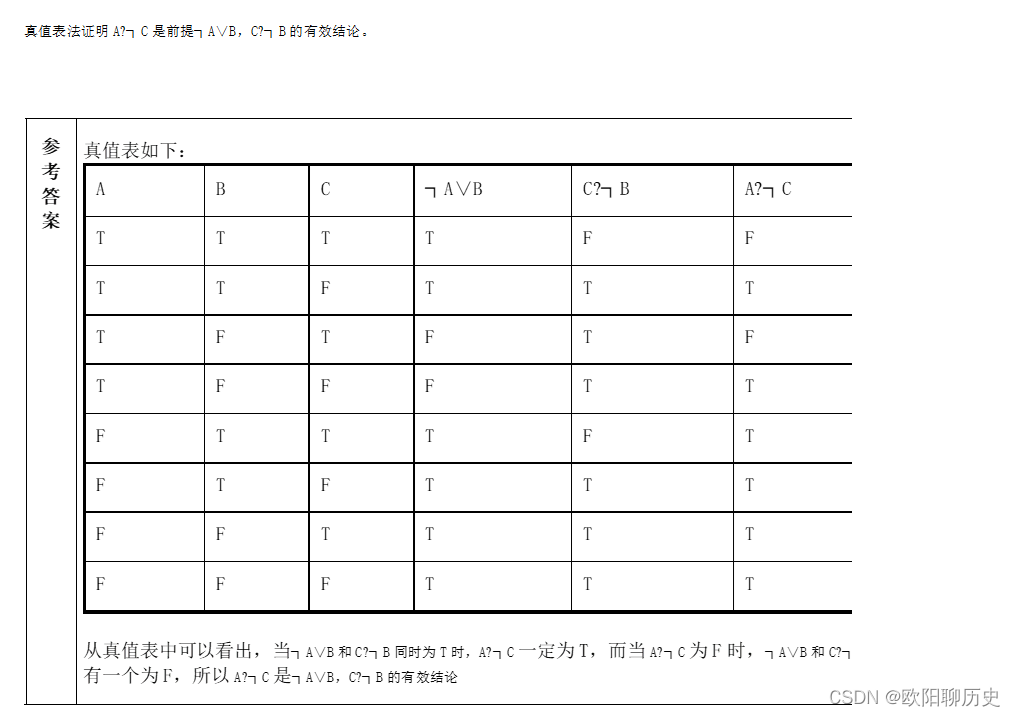
1.真值表法证明A┐C是前提┐A∨B，C┐B的有效结论。

2. 试证明：设π={A1，A2，…，An}是集合A的一个划分，定义R={<a，b>︱a、b∈Ai，i=1，2…，n}，则R是A上的等价关系.

3.图G=<V, E>，其中V={a, b, c, d, e, f }，E={(a, b), (a, c), (a, e), (b, d), (b, e), (c, e), (d, e), (d, f), (e, f)}，对应边的权值依次为5，2，1，2，6，1，9，3及8．

（1）画出G的图形；
（2）写出G的邻接矩阵；
（3）求出G权最小的生成树及其权值．

4.设A和B是全集E的子集，

5.G为n阶无向简单图，边数m=(n-1)(n-2)/2+2，证明G是汉密尔顿图。

参考答案 证明：根据汉密顿图的判别条件，在无向简单图G=<V,E>中，若能找到u,v两个顶点，使得deg(u)+deg(v)>=|V| ，则G是哈密顿图。
在该题中，|v|=n，首先，所有顶点的度数之和为：
2E=(n-1)(n-2)+4=nn-3n+6
其次，在该图中，任意去掉两个顶点u和v后，一个有(n-2)个顶点的无向完全图来说，共有(n-2)(n-3)/2条边，即一个有(n-2)个顶点的无向图中所有点的度数之和最大为(n-2)(n-3)=nn-5n+6，所以，与顶点u和v相关的边的度数之和大于等于(nn-3n+6)-(n*n-5n+6)=2n，即deg(u)+deg(v)>=n。所以G是哈密顿图。

6.设<G,>为一群。证明：若对任意a 有 ，则<G,>为阿贝尔群。

7.设A，B，C 是三个任意集合，求证: (A∪B)∩(B∪C)∩(C∪A)=(A∩B)∪(B∩C)∪(C∩A)

8.设R为实数集，σ:R×R,σ(x,y)=x+y,又τ:R×R→R,τ(x,y)=x?y，试证明σ和τ都是满射，而不是单射。

参考答案 证明：对于任意a∈R，可以使a=x+y成立的x,y有无数对，且(x,y)∈R×R，也就是说值域R中每个元素都有无数原象在R×R中，所以σ是满射，而不是单射。
对于任意a∈R，能使a=x?y成立的x,y也不止一对实数存在。例如a=6，而x=2,y=3，或
x=3,y=2,?，即象集中每一元素都有原象，而且原象不唯一，所以τ是满射，而不是单射。
证毕。

9.设给定集合A上的等价关系R，请证明：对于a,b∈A有aRb当且仅当[a]R=[b]R。

10.证明任何阶大于1的简单无向图必有两个结点的度相等。

参考答案 证明：设简单无向图G有n个结点，则每个结点的度最多为n-1。如果存在某个
结点的度为n-1，则任何结点都不可能为孤立点，于是，任何结点的度均大于等于1，小于等于n-1，由抽屉原理知，这样的n个数中至少有两个是相同的。所以必有两个结点的度相等。

11.用CP规则证明：?x(A(x)→B(x) )=>?xA(x)→?xB(x)

12.设整数集Z上的二元关系R定义如下：R={<x,y>|x,y∈Z,(x-y)/2是整数}，证明R在Z上是自反的。

参考答案
证明: ?x∈Z,(x-x)/2=0,，即<x,x>∈R，故R是自反的。

13.若无向图G中只有两个奇数度结点，则这两个结点一定是连通的。

参考答案
用反证法．设G中的两个奇数度结点分别为u和v．假设u和v不连通，即它们之间无任何通路，则G至少有两个连通分支G1，G2，且u和v分别属于G1和G2，于是G1和G2各含有一个奇数度结点．这与定理3.1.2的推论矛盾．因而u和v一定是连通的。

14.设<R,>是一个代数系统，是R上的一个二元运算，使得对于R中的任意元素a,b都有 ab=a+b+a?b，试证明：0是幺元且<R,>是独异点。
设<R,>是一个代数系统，是R上的一个二元运算，使得对于R中的任意元素a,b都有 ab=a+b+a?b，试证明：0是幺元且<R,>是独异点。
参考答案
对任意? a∈R，有
0a=0+a+0?a=a
a0=a+0+a?0=a
故0是幺元。
对任意? a,b∈R，有
ab=a+b+a?b∈R
所以是封闭的。
对任意? a,b,c∈R，有
(ab)c=(a+b+a?b)+c+(a+b+a?b)?c=a+b+c+a?b+ a?c+b?c+ a?b?c
a(bc)=a+(b+c+b?c)+a?(b+c+b?c)=a+b+c+a?b+ a?c+b?c+ a?b?c
所以(ab)c=a(bc)
故是可结合的。
综上所述，<R,>是独异点。

15.设<G,>是群，对任一a ∈G，令H={y | ya=ay,y∈G}，试证明：<H,>是<G,*>的子群。

设<G,>是群，对任一a ∈G，令H={y | ya=ay,y∈G}，试证明：<H,>是<G,>的子群。
参考答案 证明:显然HG.运算在H中满足结合律。
? p,q∈H, a ∈G
pa=ap, qa=aq
故(pq)a=p(qa)=p(aq)=(pa)q=(ap)q=a(pq)
从而pq∈H。这说明H对运算是封闭的。
由于ea=ae，所以e∈H。
对于任意的p∈H，由于pa=ap，有
p-1(pa)p-1=p-1(ap)p-1
所以ap-1=p-1a,故p-1∈H。
综上所述，<H,>是<G,*>的子群。

16.证明K3,3图不是平面图。

17.设<A,>半群，e是左幺元且对每一个 x∈A，存在x-1∈A，使得x-1x=e。

a)证明：对于任意的a,b,c∈A，如果ab=ac，则b=c。
b)通过证明e是A中的幺元，证明<A，>是群。
设<A,>半群，e是左幺元且对每一个 x∈A，存在x-1∈A，使得x-1x=e。
a)证明：对于任意的a,b,c∈A，如果ab=ac，则b=c。
b)通过证明e是A中的幺元，证明<A，>是群。

参考答案 证明：a)对于任意的a,b,c∈A
由e是左幺元，得b=eb=b
因为是半群，所以是可结合的
又因为a-1a=e 和ab=ac
所以b=eb=a-1ab=a-1ac=ec=c
b)对任意a∈A
a-1(ae)= (a-1a)e=ee=e=a-1a
所以ae= a
因此e也是右幺元。
e既是左幺元又是右幺元，e是幺元得证。
(aa-1)a=a(a-1a)=ae=a=ea
所以aa-1=e
a-1a= aa-1=e
也就是说任意a∈A均有逆元a-1。
综上所述，<A，>是群。

18.设G={a,b,c,d,e}，G上的二元运算*如表所示。

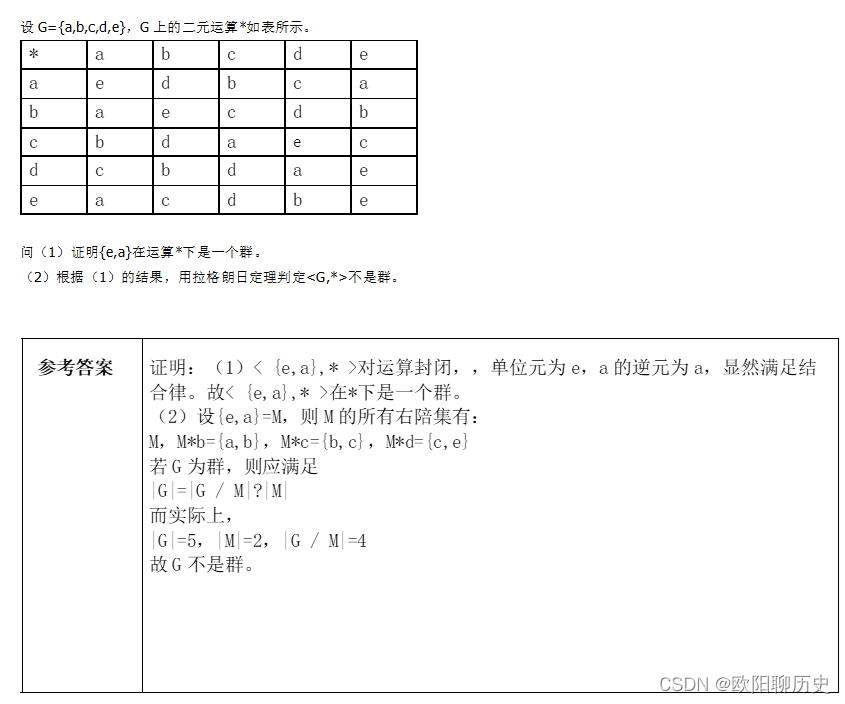
19.证明：有限整环必定是域。

20.设集合A={x,y,z}，集合B={a,b,c,d,e}，R是集合A上的关系，S是A→B上的关系。

R={<x,x>,<x,z>,<y,x>,<y,y>,<z,x>,<z,y>,<z,z>}
S={<x,a>,<x,d>,<(y,a>,<y,c>,<y,e>,<z,b>,<z,d>}
试证明： M(R?S）-1=MS-1?MR-1