单源最短路径问题（Dijkstra算法）

1、问题描述

给定一个带权有向图G=（V,E），其中每条边的权是一个实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和，这个问题通常称为单源最短路径问题。该问题的经典求解方法为迪克斯特拉算法，该算法基于贪心法进行设计，能够有效求解单源最短路径问题。

2、问题提炼

（1）给定带权有向图G =(V,E)，其中每条边的权是非负实数。（V是顶点集合，E是边集合）

（2）给定V中的一个顶点，称为源。

（3）计算从源到所有其它各顶点的最短路长度。这里路的长度是指路径上各边权之和。

3、算法选择

我选择的是Dijkstra算法：是解单源最短路径问题的贪心算法。

**贪心算法的基本要素：

（1） 贪心选择性质

指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。

这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

（2） 最优子结构性质

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。

拿单源最短路径当例子，从顶点5到顶点1的最短路径假设是5->4->2->1，那么，顶点4到1的最短路径一定是4->2->1，顶点2到1的最短路径一定是2->1。这种性质就叫做最优子结构性质。

问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

4、基本思想

（1）一个顶点属于集合S，当且仅当从源到该顶点的最短路径长度已知。

（2）设置顶点集合S，并不断地作贪心选择来扩充这个集合。

（3）贪心策略：每次都从V-S中找出具有最短特殊路长的顶点u加入S。

5、设计思路

（1）初始时，S中仅含有源点。

（2）设u是G的某一个顶点，把从源点到u且中间只经过S中顶点的路称为从源点到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。

（3）Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。

（4）一旦S包含了V中所有顶点，dist就记录了从源到其它所有顶点之间的最短路径长度。

6、算法步骤

   一、初始化：

（1）设定源点 s，将源点到自身的距离设置为 0，即 dist[s] = 0，对于其他顶点 v（v ≠ s），将距离初始化为无穷大（在程序中通常用一个足够大的数值表示），即 dist[v] = ∞。

（2）记录每个顶点的前驱顶点（用于后续回溯最短路径），初始时都设为 null。

（3）创建已确定最短路径的顶点集合 S，初始为空；未确定最短路径的顶点集合就是图中所有顶点组成的集合，记为 V - S。

   二、迭代过程：

（1）从 V - S 集合中找出距离源点 s 最短的顶点 u，将 u 加入到 S 集合中。

（2）对于顶点 u 的每一个邻接顶点 v：

计算经过 u 到达 v 的路径长度 new_dist = dist[u] + w[u][v]（这里 w[u][v] 表示从 u 到 v 边的权值）。

如果 new_dist < dist[v]，则更新 v 到源点的距离，即 dist[v] = new_dist，并且将 v 的前驱顶点设置为 u，即 prev[v] = u。

（3）重复步骤 2，直到 V - S 集合为空，此时所有顶点都已加入 S 集合，各顶点到源点的最短路径长度以及对应的前驱顶点都已确定。

7、算法设计

          

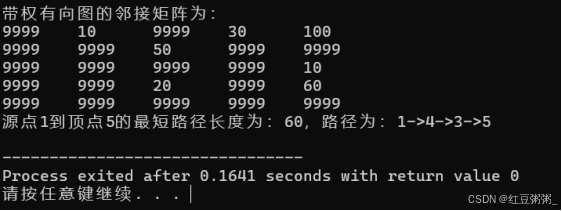
2、运行结果