大数定律和中心极限定理

大数定律

        大数定律的本质其实就是证明了在n很大的时候，样本均值依概率收敛于总体期望。

（1）切比雪夫大数定律

        条件：A）相互独立的随机变量序列，B）方差均值存在，且方差DXi 都是由上界的，即都小于等于某个数。

        那么样本均值 就会依概率收敛于  每个随机变量期望的均值

（2）辛钦大数定律

        条件：A）独立同分布的随机变量序列，B）期望存在，为u。

        辛钦大数定律是在独立同分布情况下发生的，且只需要期望存在，这是与切比雪夫大数定律的区别。正式因为有了独立同分布，所以每一个随机变量的期望都是u，且所有期望的均值也是u

        那么有 样本均值 依概率收敛于  = u

（3）伯努利大数定律

         伯努利大数定律是辛钦大数定律的特殊情况，在确定了{Xn}全部都是独立同0-1分布情况下所有的情况。

        由于二项分布中的随机变量的取值只有：0,1两种情况，所以样本均值 就变成了在n此伯努利试验中，试验成功的次数（Un表示次数），即，而此时0-1分布的总体期望是p，所以就有：

                样本均值  = 依概率收敛于 = p

中心极限定理

        中心极限定理的本质是样本均值以总体期望为中心变动，当n很大的时候，样本均值

服从的是：以总体期望为期望的，以总体方差的为方差的正太分布。

        即 样本均值服从正太分布N（,）

        即  服从正太分布N（,）

（1）列维-林德伯格定理

        条件：1）随机变量序列独立同分布 ，2）总体均值和总体方差都存在，且分别为 和

         随后可以对样本均值和n倍的样本均值进行单位化，就有了下列的公式：

                 

                 即 

    

（2）拉普拉斯定理

        拉普拉斯定理是林德伯格定理的一种特殊情况，其中的随机变量序列{Xn}满足独立同0-1分布。

         

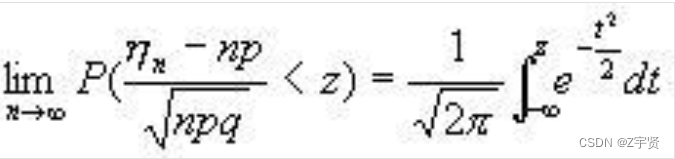
 上述是  的情况。

 样本均值服从正态分布N（,）

        即  服从正态分布N（,）

大数定律和中心极限定律的关系

        大数定律告诉你 样本均值趋向的方向是没有错的，即依概率收敛于每个随机变量期望的均值。但趋向的过程是怎么样的呢？中心极限定律就告诉你，样本均值在趋向的过程中，是服从某个正态分布的。