动态规划入门学习

本文内容主要来自于下面的链接，推荐大家观看学习动态规划(dp)入门 | 这tm才是入门动态规划的正确方式! | dfs记忆化搜索 | 全体起立!!_哔哩哔哩_bilibilid

引入：跳台阶问题

这个问题应该都很熟悉，大一的时候一般会当作例题来学函数递归

常规解法会得到一个时间复杂度O(2^n)的算法，分析发现有一半的递归是不必要的

暴力搜索

#include <iostream>

using namespace std;

int n;
int dfs(int x){
    if(x==1) return 1;
    else if(x==2) return 2;
    else{
        return dfs(x-1)+dfs(x-2);
    }

}

int main(){

    scanf("%d",&n)
    printf("%d",dfs(n));

    return 0;
}

记忆化搜索

通过记忆每一级台阶的方案数，达到递归树剪枝的效果

记忆化搜索 = dfs + 记录答案

#include <iostream>
using namespace std;
int mem[20];//记忆数组，空间换时间
int n;
int dfs(int x){
    if(mem[x]) return mem[x];//有记忆直接返回

    int sum = 0;
    if(x==1) sum = 1;
    else if(x==2) sum = 2;
    else{
        sum = dfs(x-1)+dfs(x-2);
    }
    mem[x] = sum;//记忆当前台阶方案总数
    return mem[x];
}

int main(){
    scanf("%d",&n);
    printf("%d",dfs(n));
    return 0;
}

递推（dp）

常用的递归从树根“递”到树的叶子，再由叶子“归”到根，但若是我们已有叶子节点的结果，是不是能只执行“归”的过程，从而达到递推到所需答案的效果（有点像数列的递推方程），使用迭代的方法

递推的公式 = dfs向下递归的公式

递推公式的初始值 = 递归的边界（出口）

#include <iostream>
using namespace std;

int f[20];

int main(){
    scanf("%d",&n);

    f[1] = 1;f[2] = 2;
    for (int i = 3; i <= n; i++)
    {
        f[i] = f[i-1] + f[i-2];
    }
    printf("%d",f[n]);
    // printf("%d",dfs(n));
    return 0;
}

还可以进一步优化空间，不用数组，用三个变量也可以得到答案，这里不在赘述

第一题：打家劫舍

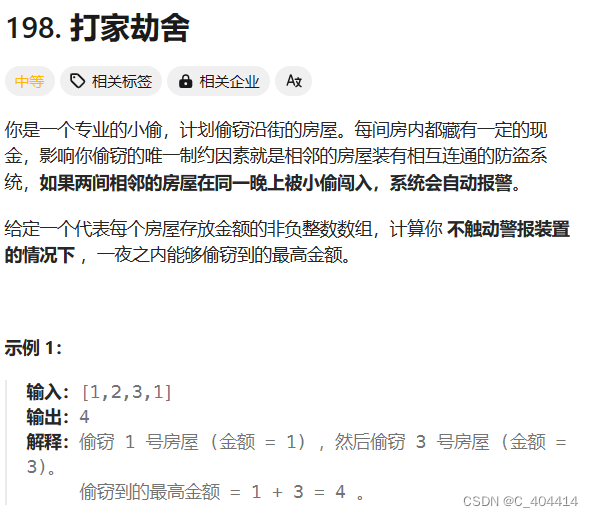
暴力搜索

不是完全按力扣的输入输出和模板写的

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

const int N = 100000;
int n;
int store[N];


int dfs(int x){
    if(x>n) return 0;
    else return max(dfs(x+1),dfs(x+2)+store[x]);
}
int main(){
    scanf("%d",&n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d",&store[i]);
    }
   cout<<dfs(1); 
    
    return 0;

}

记忆化搜索

按记忆化搜索的模板写，但是要注意记忆化搜索要注意实现记忆化搜索时要尽可能减少dfs的参数，方便实现记忆化搜索，因为记忆数组的下标数对应的是dfs的参数数，数组就是记录了函数的返回值

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100000;
int n;
int store[N];
int mem[N];

int dfs(int x){

    if(mem[x]) return mem[x];
    int sum = 0;
    if(x>n) sum = 0;
    else sum = max(dfs(x+1),dfs(x+2)+store[x]);

    mem[x] = sum;
    return sum;
}

int main(){
    scanf("%d",&n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d",&store[i]);
    }

   cout<<dfs(1); 
    
    return 0;

}

递推

递推公式就是上面dfs返回的式子

由此来写递推的代码

#include<iostream>
using namespace std;
const int N = 150;
int n;
int store[N];
int f[N];

int main(){
    scanf("%d",&n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d",&store[i]);
    }
    for (int i = n; i >= 1; i--)
    {
        f[i] = max(f[i+1],f[i+2]+store[i]);
    }
    cout<<f[1]; 
    
    return 0;

}

leecode正解

上面哪些步骤都做下来之后，其实就很容易做出这道题了

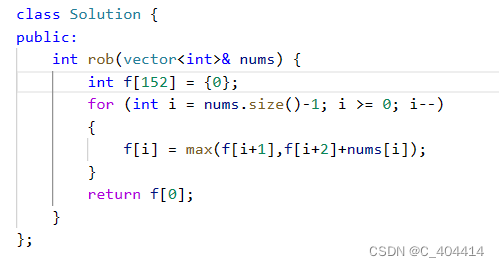
完全的代码

#include<iostream>
#include<vector>
using namespace std;

class Solution {
public:
    int rob(vector<int>& nums) {
        int f[152] = {0};
        for (int i = nums.size()-1; i >= 0; i--)
        {
            f[i] = max(f[i+1],f[i+2]+nums[i]);
        }
        return f[0];
    }
};

int main(){
    vector<int> nums;
    int item;
    while (scanf("%d",&item)!=EOF)
    {
        nums.push_back(item);
    }
    Solution S;
    cout<<S.rob(nums);
    

    return 0;

}

第二题：数字金字塔

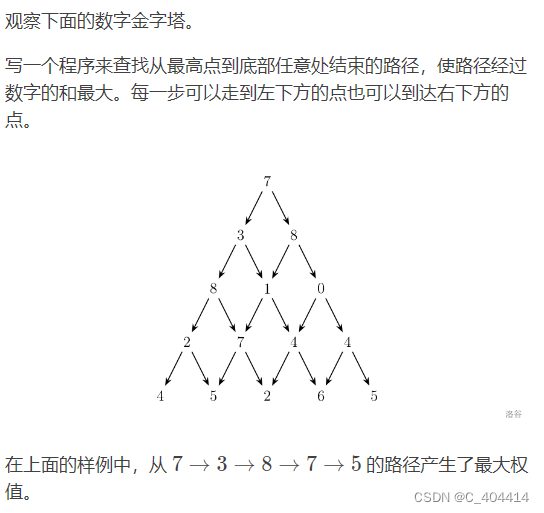
重启了一下电脑忘记保存了，导致这题写的东西丢失了，直接看代码吧

记忆化搜索+DP

对DP进行了一次内存优化，由二维降到了一维

#include <iostream>
#include <math.h>
using namespace std;
int n = 0;
int temp = 0;
int mem[1001][1001];
int arr[1002][1002];
int f[1001];


int dfs(int i,int j){

    if(mem[i][j]) return mem[i][j];

    int sum = 0;
    if(i > n) 
        sum = 0;
    else 
        sum = max(dfs(i+1,j)+arr[i][j],dfs(i+1,j+1)+arr[i][j]);

    mem[i][j] = sum;
    return mem[i][j];

}

int main(){

    scanf("%d",&n);
    
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= i; j++)
        {
            scanf("%d",&arr[i][j]);
        }
        
    }
    for (int i = n; i >= 1; i--)
    {
        for (int j = 1; j <= i; j++)
        {
            f[j] = max(f[j]+arr[i][j],f[j+1]+arr[i][j]);
        }
        
    }
    
    cout<<f[1];
    cout<<dfs(1,1)

    return 0;
}

第三题：背包问题

记忆化搜索

#include <iostream>
#include<math.h>

using namespace std;

#define MAX 1010
int arr[MAX][2];
int n,b;
int mem[MAX][MAX];
int f[MAX][MAX];

int mymax(int a,int b,int c){
    if(a>=b&&a>=c){
        return a;
    }
    else if(b>=a&&b>=c){
        return b;
    }
    else{
        return c;
    }
}

int dfs(int i,int b){
    if(mem[i][b]) return mem[i][b];
    int sum = 0;

    if(i>n) sum = 0;
    else if(arr[i][0]>b){
        sum = dfs(i+1,b);
    }
    else if(arr[i][0]<=b){

        sum = mymax(dfs(i+1,b-arr[i][0])+arr[i][1] ,dfs(i,b-arr[i][0])+arr[i][1] , dfs(i+1,b) );
    }
    mem[i][b] = sum;
    return mem[i][b];
    
}

int main(){

    scanf("%d %d",&n,&b);
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j < 2; j++)
        {
            scanf("%d",&arr[i][j]);
        }

    }
    
    cout<<dfs(1,b);

    return 0;
}

记忆化搜索已经AC

---------------------------------更新中-----------------------------------------