作者 | 浮城大亨 编辑 | 汽车人
原文链接：https://zhuanlan.zhihu.com/p/431489290
点击下方卡片，关注“自动驾驶之心”公众号
ADAS巨卷干货，即可获取
点击进入→自动驾驶之心【目标跟踪】技术交流群
本文只做学术分享，如有侵权，联系删文
问题描述
卡尔曼滤波模型假定系统状态由 t-1 时刻发展到 t 时刻，
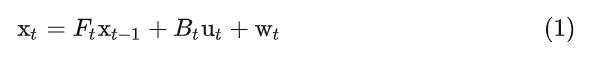
其中 是系统 t 时刻的状态向量，包含重要信息，例如位置，速度，朝向等；
是控制输入向量，例如转向角，油门控制，刹车力等；
是状态转移矩阵， t-1 时刻的状态量作用于 t 时刻的系统状态，例如 t-1 时刻的位置和速度影响着 t 时刻的位置；
是控制矩阵，控制输入影响系统状态，例如油门影响着速度和位置；
是状态向量的过程噪声，假定是均值为 0 的多元正态分布，其协方差矩阵为 。系统观测如下，
其中 是观测向量；
是变换矩阵，将状态向量映射到观测领域；
是观测向量的过程噪声，假定是均值为 0 的多元正态分布，其协方差矩阵为 。
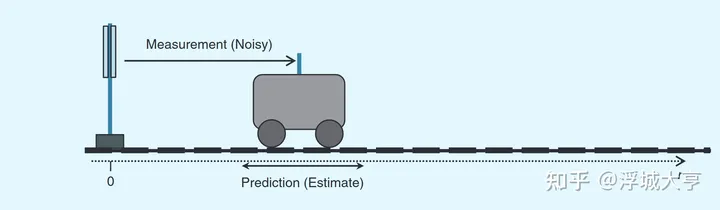
考虑一个一维系统，如图 1 所示。状态向量 包含火车的位置和速度，
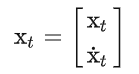
列车员会施加减速或加速控制，假定是施加力 和火车质量 m 的函数，
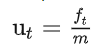
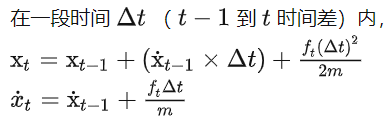
上述线性方程组可以写成矩阵形式，
但是无法直接观测到 真值，卡尔曼滤波通过融合系统模型和噪声参数来估计 ，状态参数的值表达为概率密度函数（PDF），而不是离散的值。为了描述高斯函数，需要知道方差和协方差，这些都保存在协方差矩阵 中，其对角线上元素是状态向量的方差，其他是状态向量之间的协方差。
卡尔曼滤波包括两个步骤：预测和观测更新。预测方程为
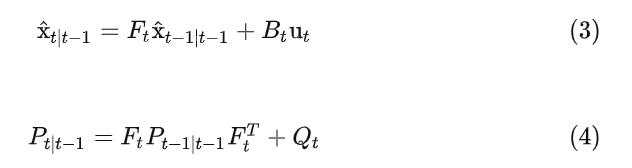
其中 是有噪声的控制量的过程噪声协方差矩阵。
式（3）可直接推导出，式（4）的推导如下。
其中
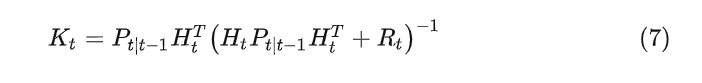
求解
每一观测时刻都想知道火车位置的最优估计，信息有两个来源：根据上一已知位置和速度的预测；火车上无线电观测。
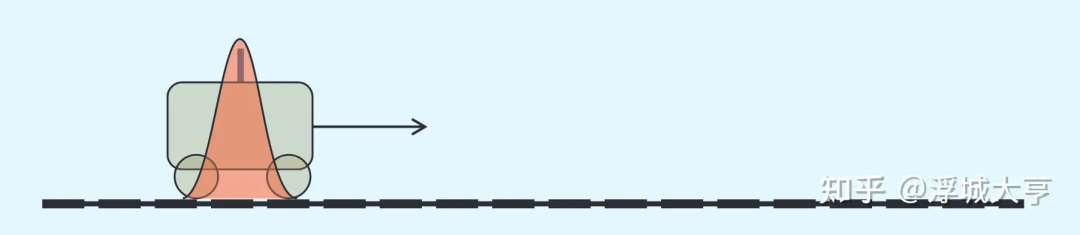
如图 2 所示，系统初始状态（t=0s）有已知精度，在下一时刻（ t=1s ）依据初始位置、速度、最大加速度和减速度等信息来估计其新位置，例如图 3 所示，方差增大了，表示不确定度增加了。
在 t=1 时刻，也通过火车上无线电观测给出火车位置，如图 4 中蓝色高斯 pdf。
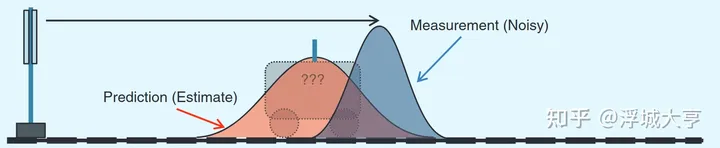
能给出的火车位置最优估计是将两个 pdf 相乘，如图 5 中绿色 pdf。
高斯函数有一关键性质：两个高斯函数的乘积仍然是高斯函数。因此它允许无限制高斯 pdf 相乘，并且结果不增大复杂度，每个时刻都有一个新的高斯 pdf。图 3 中预测的红色高斯分布为
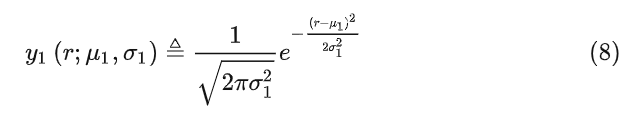
图 4 中观测的蓝色高斯分布为
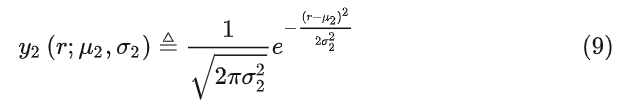
图 5 中融合预测和观测的高斯分布为
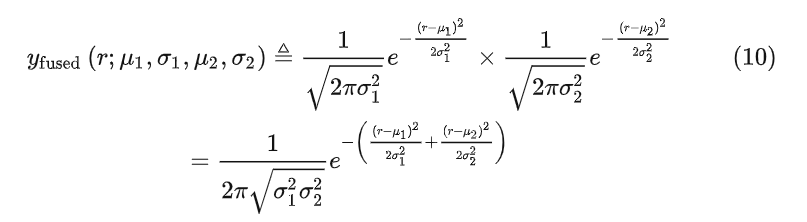
重写一下为
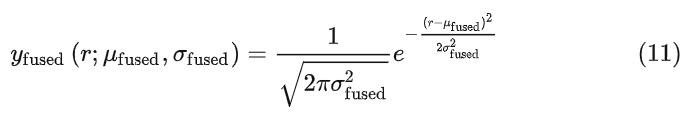
其中
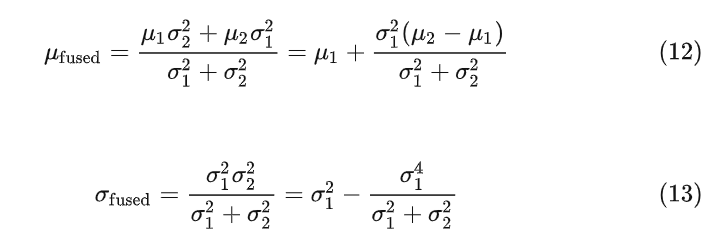
上式给出了卡尔曼滤波更新步骤，但是对于一般情况，需要扩展公式。
上面例子假定预测和更新在同一坐标系下，但是实际中需要变换矩阵 将预测转到观测空间下（统一度量衡）。重回式（8）和（9），将 分布视为 TOF，因此要把 转到 空间，
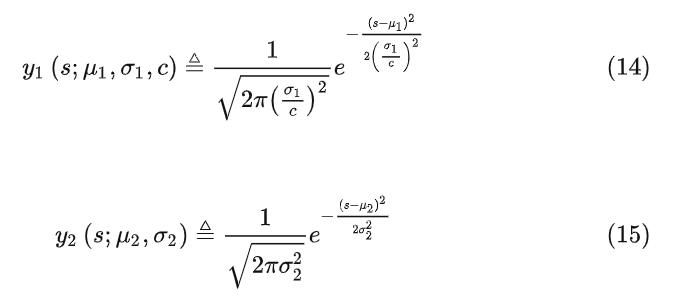
两个高斯分布都是在观测领域下，即时间 ，于是有
https://courses.engr.illinois.edu
① 全网独家视频课程
BEV感知、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、点云3D目标检测、目标跟踪、Occupancy、cuda与TensorRT模型部署、协同感知、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频（扫码即可学习）
视频官网：www.zdjszx.com
② 国内首个自动驾驶学习社区
近2000人的交流社区，涉及30+自动驾驶技术栈学习路线，想要了解更多自动驾驶感知（2D检测、分割、2D/3D车道线、BEV感知、3D目标检测、Occupancy、多传感器融合、多传感器标定、目标跟踪、光流估计）、自动驾驶定位建图（SLAM、高精地图、局部在线地图）、自动驾驶规划控制/轨迹预测等领域技术方案、AI模型部署落地实战、行业动态、岗位发布，欢迎扫描下方二维码，加入自动驾驶之心知识星球，这是一个真正有干货的地方，与领域大佬交流入门、学习、工作、跳槽上的各类难题，日常分享论文+代码+视频，期待交流！
③【自动驾驶之心】技术交流群
自动驾驶之心是首个自动驾驶开发者社区，聚焦目标检测、语义分割、全景分割、实例分割、关键点检测、车道线、目标跟踪、3D目标检测、BEV感知、多模态感知、Occupancy、多传感器融合、transformer、大模型、点云处理、端到端自动驾驶、SLAM、光流估计、深度估计、轨迹预测、高精地图、NeRF、规划控制、模型部署落地、自动驾驶仿真测试、产品经理、硬件配置、AI求职交流等方向。扫码添加汽车人助理微信邀请入群，备注：学校/公司+方向+昵称（快速入群方式）
④【自动驾驶之心】平台矩阵，欢迎联系我们！
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
