数据结构课程设计（五）反距离加权法插值

5 反距离加权法插值

5.1 需求规格说明

【问题描述】

插值是数据处理的常用手段，反距离加权插值（IDW）是一种常用而简便的空间插值方法，它以插值点与样本点间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大。

具体方法是：给出一系列平面上的点，构成插值空间。选择想要获取的属性的未知点，以此点为中心进行四邻域遍历，当遍历点数为m时，停止遍历。将遍历获取点按照插值点与样本点之间距离进行加权插值。

反距离加权参考资料：GIS中的反距离加权法插值算法 | 麻辣GIS

【输入格式】

第一行即输入点的总数n，第二行输入插值所需临近点的个数m。接下来n行依次给出各点的横纵坐标和属性值，横坐标、纵坐标、属性值间用空格分隔，构成插值空间。输入想要获取的未知的点横纵坐标。

【输出格式】

输出输入未知点的属性值。

可基于界面编程将凸包可视化。要求算法代码和界面代码分离。

5.2 总体分析与设计

（1）设计思想

①存储结构

在反距离加权法插值（IDW）的实现中，我采用了以下存储结构：

QVector<QPointF> points_：用于存储所有已知点的坐标，其中QPointF是Qt框架中用于表示二维点的类。

QVector<double> attributes_：用于存储与已知点对应的属性值。

int m_：表示在进行插值时考虑的最近邻点的数量。

这些结构简单而高效，能够快速访问和处理空间数据，便于实现IDW算法。

②主要算法思想

反距离加权法插值（IDW）的核心思想是利用已知点的属性值和它们到目标点的距离，通过加权平均的方式来估算目标点的属性值。权重通常与距离的倒数成正比，即距离目标点越近的已知点对插值结果的影响越大。

距离计算：首先计算目标点与所有已知点之间的欧几里得距离。

权重分配：然后根据距离计算每个点的权重，通常采用距离的倒数或倒数的幂次（由参数m控制）。

加权平均：最后按照计算出的权重对已知点的属性值进行加权平均，得到目标点的插值结果。

（2）设计表示

反距离加权法插值的UML类图如图5.2-1所示。

图5.2-1 程序UML类图

程序中主要设计了两个类，其中Question_5类继承自QMainWindow，主要实现了文本数据的加载和可视化操作，而IDW类主要就是实现了反距离加权算法。

（3）详细设计表示

反距离加权法插值的程序流程图如图5.2-2所示。

图5.2-2 反距离加权法插值流程图

该程序的流程步骤如下所示：

1.初始化：创建IDW对象时，传入已知点的坐标、属性值和参数m。

2.距离计算：对于目标点与每个已知点，使用欧几里得距离公式计算距离。

3.权重计算：根据距离和参数m计算每个点的权重。

4.插值计算：使用权重和已知点的属性值计算目标点的插值结果。

5.结果输出：返回计算得到的插值结果。

5.3 编码

【问题1】：如何改进算法？通过对每个点计算距离，然后排序，选取最近点。本题算法中最耗时的就是排序过程，快速排序算法时间复杂度最好也在O(nlogn)，最坏情况下时间复杂度为O(n2)，而本题提供数据已经达到两万八千条，使用原始方法计算效率十分低效。

【解决方式】：本题采用通过设定一个搜索半径radius。在这个搜索半径内查找输入点，如果找到的点的数量少于m（需要的最近邻点的数量），那么就将搜索半径扩大一倍，继续搜索，直到找到足够数量的最近邻点。如果找到的最近邻点的数量超过m，那么就按照距离从小到大排序，然后只保留最近的m个点。这一步大大减少了需要待排序的点的数量，使排序速度提高。

5.4 程序及算法分析

①使用说明

打开程序后，即可出现初始化程序样式，如图5.4-1所示。

图5.4-1 初始化程序

同样，这里可以点击界面的QAction“Txt”实现文本插值，这里我预设的默认X和Y都是0，如图5.4-2所示。

图5.4-2 文本插值

当然，这里也没必要必须再原点处插值，比如可以更改一下数据，在（1,1）处插值，如图5.4-3所示。

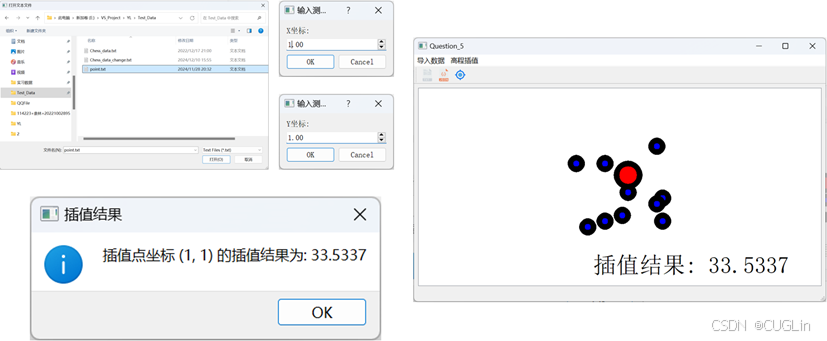
图5.4-3 更改插值点后的文本插值结果

除去文本插值，这里也支持进行在加载等高线的条件下进行插值，点击“Geojson”进行等高线可视化展示，如图5.4-4所示。

图5.4-4 等高线可视化展示

接下来，再点击“IDW”即可进行反距离加权算法的运行，这里默认输入数据经度为“102.6”，维度为“23.1”，操作如图5.4-5所示。

图5.4-5 反距离加权法插值

接下来，可以修改数据进行插值的尝试，点击“IDW”即可进行反距离加权算法的运行，这里默认输入数据经度为“102.8”，维度为“23.5”，操作如图5.4-6所示。

图5.4-6 修改数据后的反距离加权法插值

5.5 小结

IDW插值的优点是简单易用，不需要复杂的参数设定，而且能够较好地适应各种类型的空间分布。他的核心思想我觉得并不难，重点在于如何优化。本题虽然没有采用划分格网建立索引的方式，但原理类似，采用步长搜索。确定一个好的步长的基础上，甚至时间复杂度、空间复杂度都要更优。

程序在处理数据可视化时，能够根据数据点的边缘位置自动调整主窗口的比例，从而能够确保数据的清晰度和可读性。本程序采用浮点型计算，大大提高了计算的精度。一个精确的等高线图可以帮助我们更好地理解地形的特征和变化。通过使用浮点型计算，程序能够提供更准确、更可靠的数据可视化结果。

该程序还特别注重用户体验。它采用了渐变色来显示等高线，使得地形展示更加直观。这种视觉效果不仅使数据更加易于理解，还能帮助用户更快地识别出关键信息。程序具备保存计算出的点击点的位置，展示插值过程的功能，并实时更新绘图，从而实现良好的可视化效果。

然而，该程序目前尚无法二次打开文件，这在一定程度上限制了其应用范围。在未来，我们计划改进这一功能，使程序能够重复打开文件进行操作。图像标签绘制还有叠影，仍需要进行一些界面美化工作。我还将注重规范命名规则，以规范化代码。

5.6 附录

//IDW算法
IDW::IDW(const QVector<QPointF>& points, const QVector<double>& attributes, int m)
    : points_(points), attributes_(attributes), m_(m) {}

double IDW::distance(const QPointF& p1, const QPointF& p2) {
    return std::sqrt(std::pow(p2.x() - p1.x(), 2) + std::pow(p2.y() - p1.y(), 2));
}
double IDW::interpolate(const QPointF& point) {
    QVector<std::pair<double, double>> distances; // 存储距离和属性值的配对
    // 计算所有已知点与目标点之间的距离，并与属性值一起存入distances
    for (int i = 0; i < points_.size(); ++i) {
        double dist = distance(point, points_[i]);
        if (dist != 0) { // 排除与目标点重合的情况
            distances.append({ dist, attributes_[i] });
        }
    }
    // 按照距离从小到大排序
    std::sort(distances.begin(), distances.end(), [](const std::pair<double, double>& a, const std::pair<double, double>& b) {
        return a.first < b.first;
        });
    // 选择m个最近的点
    double numerator = 0.0;
    double denominator = 0.0;
    for (int i = 0; i < m_; ++i) {
        double dist = distances[i].first;
        double attr = distances[i].second;
        if (dist > 0) {
            double weight = 1.0 / std::pow(dist, 2); // 逆距离的平方作为权重
            numerator += weight * attr;
            denominator += weight;
        }
    }
    // 计算加权平均值并返回
    return numerator / denominator;
}

项目地址：Data-structure-coursework/5/Question_5 at main · CUGLin/Data-structure-courseworkhttps://github.com/CUGLin/Data-structure-coursework/tree/main/5/Question_5