树的平衡问题的引入

基本定义

参考博文

来龙去脉

**疑惑：**B树(又称B-树),B+树，B*树这么多B啥子的是要闹哪样？

首先，在数据结构中大家都知道查找，那么B树的出现是为了提高查找的效率；
我们 知道的查找主要有：顺序查找，折半查找，分块查找，树查找；前三个查找比较简单，在此就不说了，树查找，是采用树结构在进行数据查找操作；

了解
对一棵查找树（search tree）进行查询/新增/删除 等动作, 所花的时间与树的高度h 成比例, 并不与树的容量 n 成比例。如果可以让树维持矮矮胖胖的好身材, 也就是让h维持在O(lg n)左右, 完成上述工作就很省时间。能够一直维持好身材, 不因新增删除而长歪的搜寻树, 叫做balanced search tree（平衡树）。

二叉排序树（BST）引出平衡二叉树(AVL)

二叉搜索树，存在的问题是在对BST进行多次 的更新操作之后，会使BST的结构发生很大的变化。最优情况下BST的搜索性能逼近二分查找，最坏的情况下和顺序查找相当；

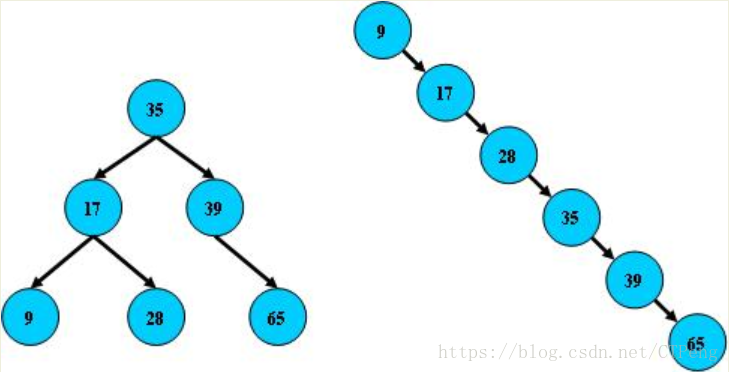
图中看到右边也是一个BST，但它的搜索性能是线性的；同样的关键字集合有可能导致不同的树结构索引；所以，使用BST还要考虑尽可能让BST保持左图的结构，和避免右图的结构，也就
是所谓的“平衡”问题；实际使用的BST基础上加上平衡算法，即“平衡二叉树”；平衡算法是平衡二叉树的关键；

平衡算法：
所谓平衡算法就是某种在B树中插入和删除结点的策略，这种策略使得B树可以保持平衡，从而保证了B树的搜索性能逼近二分查找；
平衡二叉树：
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

B树，B+树，B*树可以说是AVL的变体，主要目的就是为了进行高效的外部查找。