leetcode 1252. Cells with Odd Values in a Matrix 详解 python3

一.问题描述

Given n and m which are the dimensions of a matrix initialized by zeros and given an array indices where indices[i] = [ri, ci]. For each pair of [ri, ci] you have to increment all cells in row ri and column ci by 1.

Return the number of cells with odd values in the matrix after applying the increment to all indices.

 

Example 1:

Input: n = 2, m = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix will be [[1,3,1],[1,3,1]] which contains 6 odd numbers.

Example 2:

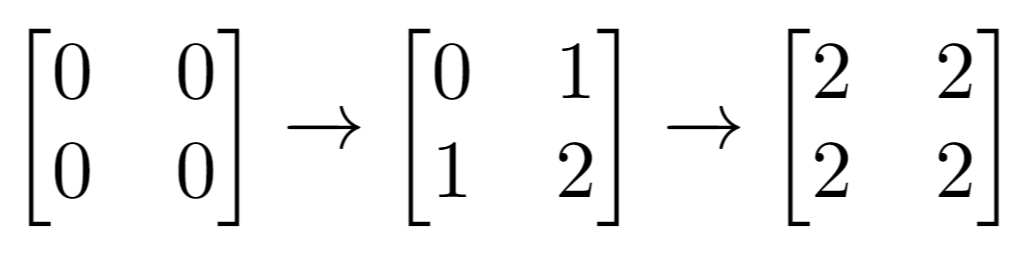
Input: n = 2, m = 2, indices = [[1,1],[0,0]]
Output: 0
Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.

 

Constraints:

• 1 <= n <= 50
• 1 <= m <= 50
• 1 <= indices.length <= 100
• 0 <= indices[i][0] < n
• 0 <= indices[i][1] < m

二.解题思路

这道题的意思就是把indices给出的那行和那列的数在原有的基础上+1。

如果用numpy有高级索引的话，这道题顺秒。

原生python的索引没有高级索引，所以只能老老实实用for循环。

处理完之后，计算数组中奇数的个数。

更新一个高效算法：

目的：计算奇数的个数

计算方法：可以统计对于nums[i][j]，即第i行第j列的值，它的值为indices中索引i,j的出现次数。

我们只需要统计i和j的出现次数和，如果和为偶数，则nums[i][j]为偶数，否则为奇数。

同时有一个优化技巧，偶数+偶数必然是偶数，偶数+奇数是奇数，奇数+奇数是偶数。

我们最后只需要知道的是他们俩和的奇偶，并不需要知道它们和具体的值，因此计算i和j在indices中出现的次数的时候，

只需要保存0或1，0偶数，1奇数，这样子可以用位运算符来做，会非常快。

更多leetcode算法题解法: 专栏 leetcode算法从零到结束

三.源码

class Solution:
    def oddCells(self, n: int, m: int, indices: List[List[int]]) -> int:
        matric=[[0]*m for i in range(n)]
        for cordinate in indices:
            r,c=cordinate[0], cordinate[1]
            matric[r]=[num+1 for num in matric[r]]
            for t in range(n):
                matric[t][c]+=1
        return sum([1 for row in matric for num in row if (num%2)!=0])

2.位运算，来自：https://leetcode.com/problems/cells-with-odd-values-in-a-matrix/discuss/425212/Simple-Python-solution

odd_count = 0
rows = [0] * n
cols = [0] * m

for i, j in indices:
	rows[i] = rows[i] ^ 1
	cols[j] = cols[j] ^ 1

for i in range(n):
	for j in range(m):
		if(rows[i] ^ cols[j] == 1): odd_count += 1

return odd_count