钰的BFS的学习笔记

最新推荐文章于 2022-03-28 14:18:37 发布

CSY�

最新推荐文章于 2022-03-28 14:18:37 发布

阅读量222

点赞数

CC 4.0 BY-SA版权

分类专栏：算法学习笔记

本文链接：https://blog.youkuaiyun.com/CSY94CFY/article/details/111319386

算法学习笔记专栏收录该内容

4 篇文章

订阅专栏

BFS（Breadth First Search）

什么是用BFS？

BFS，其英文全称是Breadth First Search。 BFS并不使用经验法则算法。从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实验里，其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为 closed 的容器中。（open-closed表）*

自然界的宽搜（想出来的真的是个天才）

为什么用BFS？

同作为搜索，相对于dfs来说，bfs是在用空间换时间。也就是说，他快啊！！！

怎么用BFS？

*用两个队列（queue）也就是open closed表存节点用来搜下一层的节点

具体见郭炜老师的mooc：https://www.icourse163.org/learn/PKU-1001894005?tid=1461679488#/learn/announce

其实大家学到这应该和我有一样的问题

dfs明明代码实现更简单，为什么要用bfs？

来拜见知乎大佬，顺便他的文章中的bfs的两个典型，也就是郭炜老师的两道经典例题

https://zhuanlan.zhihu.com/p/136183284

例题：

迷宫问题

Description

定义一个二维数组：

int maze[5][5] = {

	0, 1, 0, 0, 0,

	0, 1, 0, 1, 0,

	0, 0, 0, 0, 0,

	0, 1, 1, 1, 0,

	0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

Input

一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。

Output

左上角到右下角的最短路径，格式如样例所示。

Sample Input

Sample Output

(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)

Source

#include<bits/stdc++.h>
using namespace std;
int ma[7][7];
struct pos
{
    int r,c;
    int father;//父亲点在队列中的下标,-1 表示本节点是起点
    pos(int rr=0,int cc=0,int ff=0):r(rr),c(cc),father(ff) { }//重载pos
};
pos que[100];//队列
int head,tail;//队列头尾指针
pos dir[4]={pos(-1,0),pos(1,0),pos(0,-1),pos(0,1)};//移动方向
int main()
{
    memset(ma,0xff,sizeof(ma));
    for (int i=1;i<=5;i++)
    {
        for (int j=1;j<=5;j++)
            cin>>ma[i][j];
    }
    head=0;
    tail=1;
    que[0]=pos(1,1,-1);
    while(head!=tail)//队列不为空
    {
        pos ps=que[head];
        if(ps.r==5&&ps.c==5)//目标节点出队列
        {
            vector<pos> vt;
            while(true)
            {
                vt.push_back(pos(ps.r,ps.c,0));
                if(ps.father==-1)//起点
                    break;
                ps=que[ps.father];
            };
            for(int i=vt.size()-1;i>=0;i--)
                cout<<"("<<vt[i].r-1<<", "<<vt[i].c-1<<")"<<endl;
            system("pause");
            return 0;
        }
        else 
        {//队头节点不是目标节点
            int r=ps.r,c=ps.c;
            for (int i=0;i<4;i++)
            {
                if (!ma[r+dir[i].r][c+dir[i].c])
                {
                    que[tail++]=pos(r+dir[i].r,c+dir[i].c,head);
                    //新扩展出来的节点的父节点在队列里的下标是head
                    ma[r+dir[i].r][c+dir[i].c]=1;
                }
            }
            head++;
        }
    }
    system("pause");
    return 0;
}

抓住那头牛

农夫知道一头牛的位置，想要抓住它。农夫和牛都位于数轴上，农夫起始位置位于点`N(0≤N≤100000)`，牛位于点`K(0≤K≤100000)`。农夫有两种移动方式：

从X移动到X-1或X+1，每次移动花费一分钟
从X移动到2*X，每次移动花费一分钟

假设牛没有意识到农夫的行动，站在原地不动。农夫最少要花多少时间才能抓住牛。

策略1·深度优先搜索：从起点出发，随机挑一个方向，能往前走就往前走（扩展），走不动了则回溯。不能走已经走过的点（要判重）。
要想求最优解，则要遍历所有走法。可以用各种手段优化，比如，若已经找到路径长度为n的解，则长度大于n的走法就不必尝试。
运算过程中需要存储路径上的节点，数量较少。用栈存节点。
策略2·广度优先搜索：
给节点分层。起点是第0层。从起点最少需要n步就能到达的点属于第n层
搜索过程（节点扩展过程）：
3
2 4 6
1 5
问题解决。
扩展时，不能扩展出已经走过的节点（要判重）。
可确保找到最优解，但是因扩展出来的节点较多，且多数节点都需要保存，因此需要的存储空间较大。用队列存节点。

#include<bits/stdc++.h>
using namespace std;
int n,k;
int visited[100005];//判重标记,visited[i] = true 表示i已经扩展过
struct step
{
    int x;//位置
    int steps;//到达x所需的步数
    step(int xx,int s):x(xx),steps(s){ }
};
queue<step> q;//队列,即Open表
int main()
{
    cin>>n>>k;
    memset(visited,0,sizeof(visited));
    q.push(step(n,0));
    visited[n]=1;
    while(!q.empty())
    {
        step s=q.front();
        if (s.x==k)//找到目标
        {
            cout<<s.steps<<endl;
            return 0;
        }
        else 
        {//走x+1,x-1,x*2,
            if (s.x-1>=0&&!visited[s.x-1])
            {
              q.push(step(s.x-1,s.steps+1));//将s压进去
              visited[s.x-1]=1;
            }
            if (s.x+1<=100000&&!visited[s.x+1])
            {
                q.push(step(s.x+1,s.steps+1));
                visited[s.x+1]=1;
            }
            if (s.x*2<=100000&&!visited[s.x*2])
            {
                q.push(step(s.x*2,s.steps+1));
                visited[s.x*2]=1;
            }
            q.pop();
        }
    }
    return 0;
}

P5318 【深基18.例3】查找文献

题目描述

小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 n(n\le10^5)n(n≤105) 篇文章（编号为 1 到 nn）以及 m(m\le10^6)m(m≤106) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

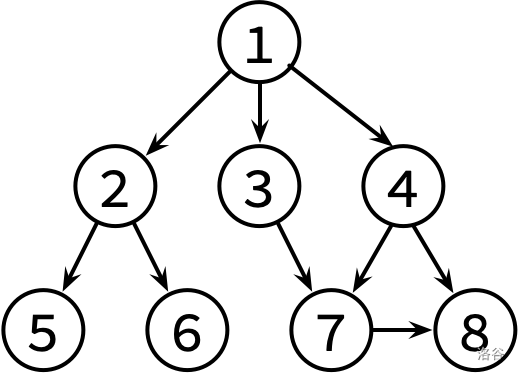
请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

无

输出格式

无

输入输出样例

输入 #1复制

输出 #1复制

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8

#include<bits/stdc++.h>
using namespace std;  
struct edge{       //存边结构体
	int u,v;
}; 
vector <int> e[100001];  //两个vector刚才已经详细讲过了
vector <edge> s;
bool vis1[100001]={0},vis2[100001]={0}; //标记数组
bool cmp(edge x,edge y){  //排序规则
	if(x.v==y.v)
	return x.u<y.u;
	else return x.v<y.v;
}
void dfs(int x){  //深度优先遍历
	vis1[x]=1;
	cout<<x<<" ";
	for(int i=0;i<e[x].size();i++){
		int point=s[e[x][i]].v;
		if(!vis1[point]){
			dfs(point);
		}
	}
}
void bfs(int x){  //广度优先遍历
	queue <int> q;
	q.push(x);
	cout<<x<<" ";
	vis2[x]=1;
	while(!q.empty()){
		int fro=q.front();
		for(int i=0;i<e[fro].size();i++){
			int point=s[e[fro][i]].v;
			if(!vis2[point]){
				q.push(point); 
				cout<<point<<" ";
				vis2[point]=1;
			}
		}
		q.pop();
	}
}
int main(){
	int n,m;  //输入，存边
	cin>>n>>m; 
	for(int i=0;i<m;i++){
		int uu,vv;
		cin>>uu>>vv;
		s.push_back((edge){uu,vv});   
	}
	sort(s.begin(),s.end(),cmp);  //排序
	for(int i=0;i<m;i++)   
		e[s[i].u].push_back(i); 
	dfs(1);   //从1号顶点开始深搜
	cout<<endl;
	bfs(1);   //广搜亦同理
}