引导方法深度补全系列—早期融合模型—5—《Depth completion via deep basis fitting》

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

创新点

一、文章概述

二、方法详解

1.网络结构

2.具体方法

总结

---

创新点

1.用最小二乘拟合模块代替大多数深度完井网络中使用的最后1×1卷积层

2.使用了非线性最小二乘法，处理实际数据中的噪声测量和异常值

---

一、文章概述

主要是替换了多变单通道的卷积层

二、方法详解

1.网络结构

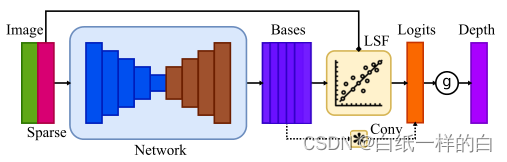
 实线表示模块的数据流，而虚线表示基线方法的数据流。baseline只是一个卷积层。我们的LSF模块可以取代卷积层，而不改变网络的其余部分。

2.具体方法

线性最小二乘法拟合模块（LSF）

*最小二乘法对异常值很敏感

模块输入多通道的特征和稀疏深度，输出单通道的结果L,一般深度估计网络最后卷积层把多通道的特征B转换为单通道结果L，称为logits层，最后一层的输入范围较大，使用非线性激活函数g将值映射到正深度，本文选择的g为

a控制最小深度的比例因子，设为1

像素的预测深度为

这个权重w通过从多通道的特征B到有效像素处的稀疏深度S的最小二乘拟合得到，替代最终卷积层

最小化最小二乘问题的目标函数为

si为单个稀疏深度，N为S中的有效像素数，此时优化的函数为

但这个函数g是非线性的，所以把变量换成g-1（）

得到新的函数之后重新整理最小二乘拟合问题，转换成矩阵形式

求解这个新的函数，用的是伪逆（Moore-Penrose），原因是B不是方阵严格意义上没有逆矩阵这个概念，所以根据伪逆的定义得到一个使得Bw与t欧式距离最小的解，也就完成了最小二乘拟合问题求解

B表示Nx（M+1）的堆叠特征矩阵，t为对应的稀疏深度向量，下一步使用λ正则化

非线性最小二乘法

这一步用于处理真值的异常值，首先对原始非线性最小二乘问题做处理

对w求导

J就是雅可比矩阵表示残差函数r对于w求导，∆w就是权重的变化，求解这个∆w

引入Cholesky 分解W=LTL其中的项和噪声成反比，引入的Huber函数为

 

求解并且迭代计算∆w，目的是更新w

w的初始化由上一小节求得，为了缓解梯度消失或梯度爆炸使用不完全优化，固定迭代次数，减少内存消耗和时间

 

自监督的多尺度训练

自监督训练把学习问题表达为视图合成，这个和深度估计类似，在多尺度上训练并对图像重建，在每个解码器层分辨率下预测深度，由于光度误差的模糊性，这会在低分辨率深度图中的大纹理区域中产生伪影。通过将所有低分辨率深度图上采样到输入图像分辨率，改进了这种方法；但这个方法在每个尺度预测的深度图是独立的，在训练阶段使用较低分辨率深度图，但在推断过程中丢弃，导致参数浪费。

本文的方法是预测一组基础的Bk，没有直接预测每个尺度的深度，然后走文章中提到的LSF模块得到最后的深度

每个基础向量都是通过对解码器中相应尺度的特征进行上采样获得的，所以对应尺度的深度预测就将尺度因子s对应起来，按需重建全分辨率深度图，然后对其进行升采样并重新分组，以执行拟合步骤

---

总结

不是在最后一层使用一组固定的权重，而是从倒数第二个特征到稀疏深度进行最小二乘拟合，以获得一组数据相关的权重