CometOJ C0210 [2012普及组-A]质因数分解（附：质数打表模板）

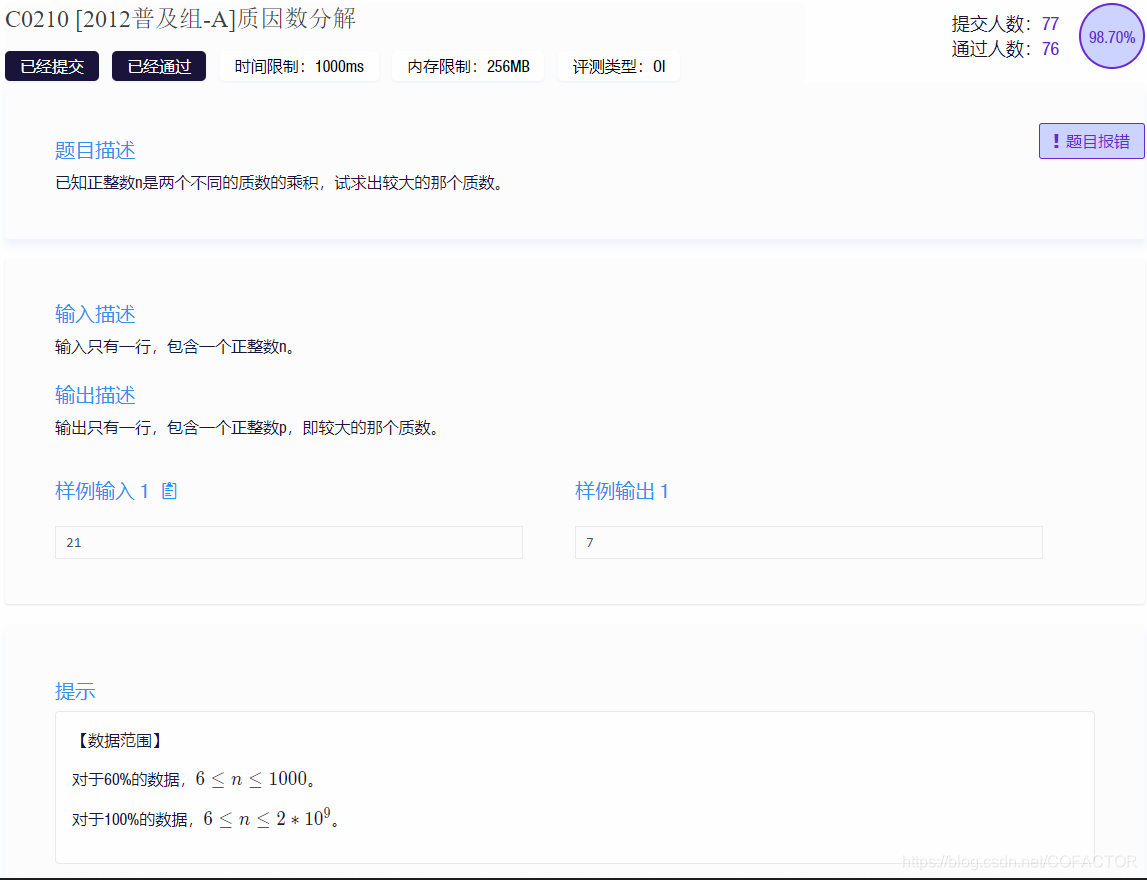
一、题目描述

二、算法分析说明

先把前 sqrt(n) 个质数算出来，方便后续分解质因数。
因为 n ≤ 2e9 ，而 sqrt(2e9) ≈ 44721 ，所以只需要求前 44721 个质数。

质数打表模板说明
设需要生成前 qty_of_prime 个质数，prime 数组用于存储已经验证为质数的数。
设 a 为当前正在验证是否为质数的正整数，t = sqrt(a) 为需要试除的范围。
用已知的质数去除 a ，如果能整除，a 就有除了 1 和 a 本身以外的因数，终止当前的判断，准备判断 a + 1 。
为什么只用试除到 t = sqrt(a) 呢，因为因数是一对一对的，例如：
100 的因数有：1 2 4 5 10 20 25 50 100
我们发现，1 * 100 == 2 * 50 == 4 * 25 == 5 * 20 == 10 * 10
如果验证到 sqrt(a) 后，还没有发现第 3 个 a 的因数，自然也不会再有了。
换句话说，还是以 100 为例子，如果找出了因数 2 ，同时就可以计算出因数 50 。如果找到了因数 4 ，就可以计算出因数 25 。
如果验证了某个数 d 不是 a 的因子，那么 d 的倍数也不是 a 的因子。
比如 2 不是 a 的因子，那么 4 6 8 …… 都不用验证了。
比如 3 不是 a 的因子，那么 6 9 12 …… 都不用验证了。
如果要验证是否为 a 的因子的数 d 是质数，那么在之前验证过的数及其倍数都不是这个质数 d 的因数，也就是说 d 还没有用于验证过。
可见，用质数试除是不能避免的。对于合数来说，如果已知它的一个质因数不是 a 的因子，那么这个合数也不用再验证是否为 a 的因子 ，
意即，要用这个合数去除 a ，就相当于用 a 的每个质因数去除 a 。如果某个质因数不能整除 a ，那么这个合数也不能整除 a 。
从几个角度都啰嗦完了，相信总有一种角度适合你的理解。

然后用已知的某个质数 p 去试除 n ，如果能整除，就输出 n / p 即为答案。

三、AC 代码

（59 ms）

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#pragma warning(disable:4996)
const unsigned long long qty_of_prime = 44721;
unsigned long long prime[qty_of_prime] = { 2, 3 };
inline void genprime() {
	unsigned long long a = 4, t; bool flag = true;
	for (unsigned long long i = 2; i < qty_of_prime;) {
		t = sqrt(a), flag = true;
		for (unsigned long long j = 0; prime[j] <= t; ++j) {
			if (a % prime[j] == 0) { flag = false; break; }
		}
		if (flag) { prime[i] = a, ++i; }
		++a;
	}
}
int main() {
	unsigned long long n;
	genprime();
	scanf("%llu", &n);
	for (unsigned long long i = 0; i < qty_of_prime; ++i) {
		if (n % prime[i] == 0) { printf("%llu\n", n / prime[i]); break; }
	}
	return 0;
}