【数字逻辑与EDA技术】数字电子技术基础-期末考试重点总结

啊，6月就要期末考试了耶，那就浅浅地复习一下下叭

---

---

---

第一章 数制和码制

一、四种进制之间的进制转换

二进制 B

八进制 O

十进制 D

十六进制 H

巧记：BODH 谐音：拨(BO)电(D)话(H)

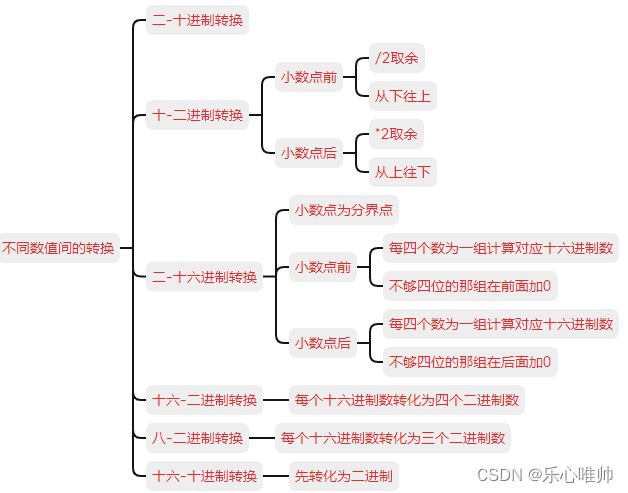
二、浮点数的进制转换

十-二转换

小数点前面的数除以二，小数点后面的数乘以二。

例：

二-十转换

小数点往前的数依次乘以2的零次方、一次方、二次方；小数点往后的数依次乘以2的负一次方、负二次方、负三次方......

例：

三、反码、补码和补码运算

  

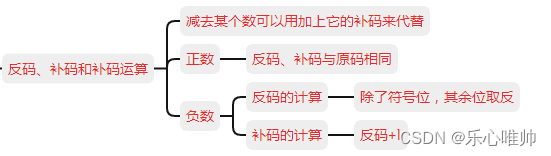
反码的求法

正数反码与原码相同，负数如果有符号位，则符号位不变，其余每个二进制位取反，即0变成1、1变成0。

补码的求法

正数补码与原码相同，负数如果有符号位，则符号位不变，其余位各位取反后，再加1；若无符号位，则直接各位取反后，再加1。

补码运算

一般是同一进制数之间的加减法

如果两个数同号，则先计算两个数的绝对值，判断出需要m个有效二进制数表示数的大小，然后再加一个符号位，也就是一共有m+1个二进制数来表示此次运算过程。

例：1101+0101，-1011-1010.

如果两个数异号，和的绝对值一定小于其中的绝对值比较大的那个绝对值，所以补码的数值部分不需要增加位数。

例：1110-0111，0111-1110.

负数的补码求原码

将此补码再求补，得到的就是原码。

四、常见的编码方式（了解即可）

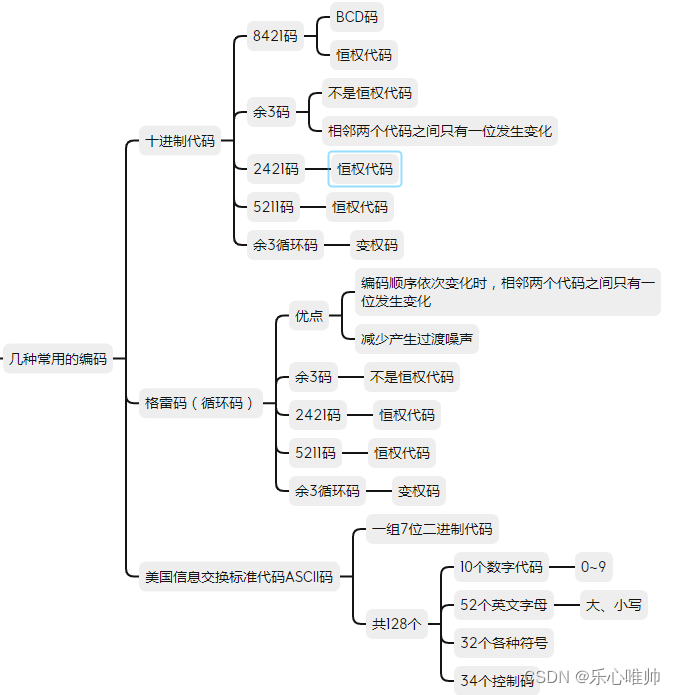
十进制代码

8421码，又称BCD码

格雷码，又称循环码

ASCII码 一组7位二进制码，共128个。

---

---

---

第二章、逻辑代数基础

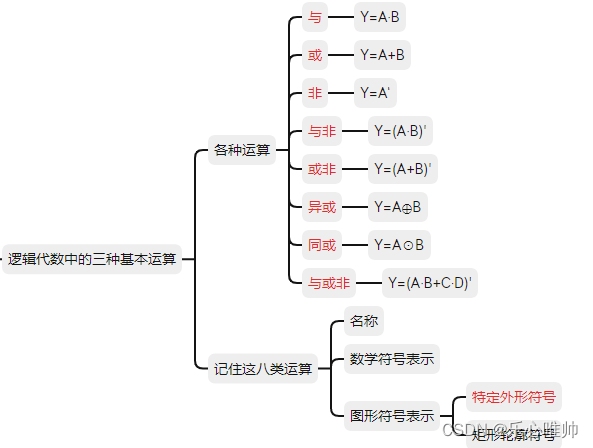
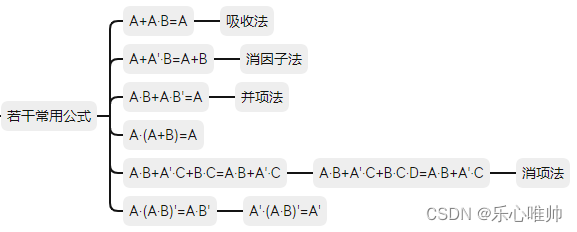
一、逻辑等式的证明

方法一：逻辑式的真值表是否相同，若相同，则等式成立。

方法二：逻辑代数的公式和定理将等式两边化成完全相同的形式，则等式成立。

方法三：分别画出等式两边逻辑式的卡诺图，若卡诺图相同，则等式成立。

二、逻辑函数不同描述方法之间的转换

真值表→逻辑式

逻辑式→逻辑图

逻辑式→卡诺图

波形图→真值表

逻辑式→真值表

逻辑图→逻辑式

其他的互相转换：利用上边的几种基本的转换方法，可以实现任意两种表示方法之间的转换。

三、逻辑函数式的变换

1、与或形式→与非-与非形式

方法：利用摩根定理将整个与或式两次求反

2、与或形式→与或非形式

方法：先画出卡诺图，将填入0的那些最小项合并、再求反。

3、与或形式→或与形式

方法一：先转化为与或非形式，然后用摩根定理。

方法二：反复运用公式A+BC=（A+B）（A+C）进行运算

4、与或形式→或非-或非形式

方法：先转化为与或非形式，再用摩根定理将与或非中的每个乘积项化为或非的形式。

5、将逻辑函数式化为最小项之和的形式

方法：先利用逻辑代数的公式和定理将函数式转化成与或形式，在利用乘（A+A'）补齐缺项

四、逻辑函数的化简

公式化简法

卡诺图化简法

多输出逻辑函数的化简（了解）

---

---

---

第三章 门电路 

二极管、三极管、CMOS反相器的识别（了解）

---

---

---

第四章 组合逻辑电路

一、数据选择器的应用（了解）

二、译码器的应用（了解）

三、加法器的应用（了解）

四、数值比较器的应用（了解）

五、编码器的应用（了解）

ps：表示反相的小圆圈在逻辑图形符号的输入端，是为了强调说明“低电平有效”。

习题类型

一、组合逻辑电路分析

分析给定逻辑电路（可能是小规模集成门电路组成，也可能是中规模集成常用组合逻辑电路组成）的功能，写出它的逻辑函数式或功能表，来让逻辑功能更加直观、明了。

二、组合逻辑电路设计

用小规模集成门电路设计组合逻辑电路

1. 进行逻辑抽象，把要求实现的逻辑功能表述为一个逻辑函数形式。
   1. 确定输入变量和输出变量。
   2. 定义逻辑状态的含义。