【noip模拟赛】 总结与反思——作业调度方案

引子：

这道题和后面一道题都将会是引子，而不是序言因为这两道题在考试的时候基本没有看，看也没有看懂。这道题给我的一个直观感受是，我的语文是真的差。连题意讲了个嘛我都不知道，我还做个what题啊。 所以考试之后读题的时候又双叕是这个心情：

以及这个心情：

所以好不容易读懂了一点点，我就是说一下我拙略的想法。

---

B——作业调度方案

题目描述：

我们现在要利用m台机器加工n个工件，每个工件都有m道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。

每个工件的每个工序称为一个操作，我们用记号j-k表示一个操作，其中j为1到n中的某个数字，为工件号；k为1到m中的某个数字，为工序号，例如2-4表示第2个工件第4道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。

例如，当n=3，m=2时，“1-1，1-2，2-1，3-1，3-2，2-2”就是一个给定的安排顺序，即先安排第1个工件的第1个工序，再安排第1个工件的第2个工序，然后再安排第2个工件的第1个工序，等等。

一方面，每个操作的安排都要满足以下的两个约束条件。

(1)对同一个工件，每道工序必须在它前面的工序完成后才能开始；

(2)同一时刻每一台机器至多只能加工一个工件。

另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。 由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为“1 1 2 3 3 2”。

还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。

例如，取n=3,m=2，已知数据如下：

工件号	机器号/加工时间	
	    工序1	工序2
1	    1/3	    2/2
2	    1/2	    2/5
3	    2/2	    1/4

则对于安排顺序“1 1 2 3 3 2”，下图中的两个实施方案都是正确的。但所需要的总时间分别是10与12。

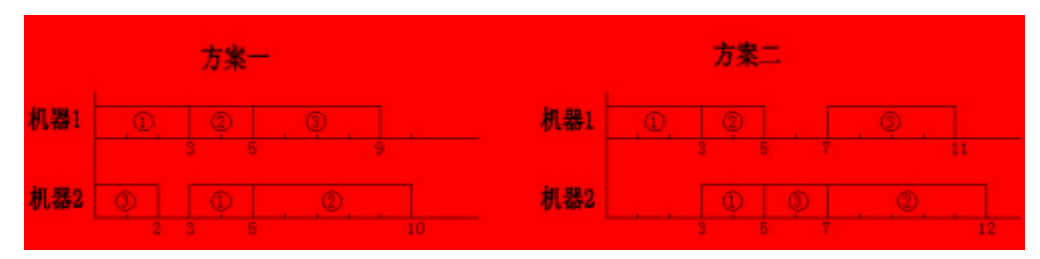
当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：在保证约束条件（1）（2）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（1）（2）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。

显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

输入格式：

输入文件jsp.in的第1行为两个正整数，用一个空格隔开：
m n（其中m（<20）表示机器数，n（<20）表示工件数）

第2行：m*n个用空格隔开的数，为给定的安排顺序。

接下来的2n行，每行都是用空格隔开的m个正整数，每个数不超过20。

其中前n行依次表示每个工件的每个工序所使用的机器号，第1个数为第1个工序的机器号，第2个数为第2个工序机器号，等等。
后n行依次表示每个工件的每个工序的加工时间。
可以保证，以上各数据都是正确的，不必检验。

输出格式：

输出文件jsp.out只有一个正整数，为最少的加工时间。

样例

输入样例：

2 3
1 1 2 3 3 2
1 2
1 2
2 1
3 2
2 5
2 4

输出样例：

10

---

思路与分析

相信大家读完题和我的感受应该是差不多的吧，由此可得强基计划还是起到了一定的作用。
但是！如果能有一张草稿纸把题目给出的条件罗列下来，然后再想（用过几个小时），这道题比较清晰了。。。（我自己都不信）
好了，不说废话了。开始分析：
因为题目告诉我们的条件已经很多了（罗列在草稿纸上的已知条件派上用场了），然后就需要我们暴力枚举工件——按照工件的优先度来。接着用一个数组来表示工件的目前最晚完成时间。为了清楚机器 i 在 j 时刻时是否处在空闲时刻，这里就可以用到一个二维bool数组flag来表示。
再接着用一个临时sum表示目前的最长空闲时间，机器开始工作，就把sum清0，进而重新寻找空隙，否则sum++,当sum>=这个工件在这道工序上要花费的时间 时，就把这一段的机器占用情况变为工作，表示工件的目前最晚完成时间的数组变为空隙的结尾进行插入操作。

---

代码：

#include<iostream>
#include<cstdio>
using namespace std;
int work[21