题目描述
请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
问题分析
这个问题的切入点是二叉树的镜像,二叉树和它的镜像相同意味着(以下图为例)根节点的左右子树相同,对a而言,左侧的a的左子树b必须等于右侧a右子树的b,余下的结点以此类推,满足这些条件才可以称为同样的。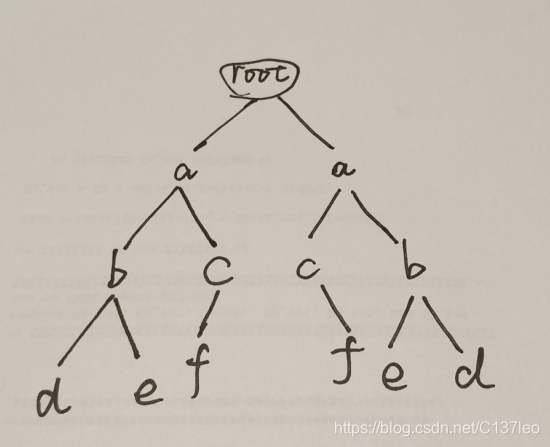
二叉树的结构
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
代码及解释
我的思路是先判断根节点是否为空或者只有一个根节点,这种情况可以认为是true
递归方法:返回类型是boolean类型,形参是当前节点的左右子结点l,r,如果这两个结点都为空则返回true,如果l,r其中有一个为null,而另一个不为null,或者l.val!=r.val则返回false,否则返回l.left和r.right的judge方法和l.right和r.left的judge方法的逻辑与的结果。以上面的图为例,在判断完左右a的val相等后,进入judge方法的递归逻辑与运算judge(l.left,r.right)&&judge(l.right,r.left);既左侧a的左子结点b和右侧a的右子节点b进行judge方法判断(还会对b结点递归),判断的结果和左侧a的右子节点c和右侧a的左子结点c进行judge方法的结果(也会对c进行递归)逻辑与,则就是问题的答案。
public class Solution {
boolean isSymmetrical(TreeNode pRoot)
{
if(pRoot==null)return true;
if(pRoot.left==null&&pRoot.right==null)return true;
return judge(pRoot.left,pRoot.right);
}
public boolean judge(TreeNode l,TreeNode r){
if(l==null&&r==null)return true;
if((l!=null&&r==null)||(l==null&&r!=null))return false;
if(l.val!=r.val)return false;
return judge(l.left,r.right)&&judge(l.right,r.left);
}
}
别人的代码
别人的代码依旧简洁优雅,我自愧不如。
public class Solution {
boolean isSymmetrical(TreeNode pRoot){
if(pRoot == null){return true;}
return comRoot(pRoot.left, pRoot.right);
}
private boolean comRoot(TreeNode left, TreeNode right){
// TODO Auto-generated method stub
if(left == null) return right==null;
if(right == null) return false;
if(left.val != right.val) return false;
return comRoot(left.right, right.left) && comRoot(left.left, right.right);
}
}
链接:https://www.nowcoder.com/questionTerminal/ff05d44dfdb04e1d83bdbdab320efbcb?f=discussion
来源:牛客网
总结
这个问题可以用递归的思想求解,我的方法中
if(pRoot.leftnull&&pRoot.rightnull)return true;这一步可以省略,后面的判断部分也写的不够优雅,继续努力向各位大佬学习,兄弟们干了,奥利给,呕。








 本文介绍了一种使用递归方法判断二叉树是否对称的Java实现。通过对二叉树的镜像特性进行分析,阐述了如何比较根节点的左右子树,确保每个节点的左右子树与其镜像节点的对应子树相等。提供了详细的代码示例和解释。
本文介绍了一种使用递归方法判断二叉树是否对称的Java实现。通过对二叉树的镜像特性进行分析,阐述了如何比较根节点的左右子树,确保每个节点的左右子树与其镜像节点的对应子树相等。提供了详细的代码示例和解释。
















 172万+
172万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








