sigmoid激活函数、Tanh激活函数、ReLU激活函数、LeakyReLU激活函数、ELU激活函数、GELU激活函数
代码
clc
clear all
x = -10:0.1:10;
%% sigmoid
f1 = figure;
set(gcf,'Position',[100,200,1100,450])
y = (1+ exp(-x)).^-1;
subplot(2,3,1),
plot(x,y);
axis([-inf,inf,-0.05,1.05])
latex = '$$sigmoid(x) = \frac{1}{1 + e^{-x}}$$';
text(-9,0.8,latex,'Interpreter','latex','FontSize',9);
title('Sigmoid');
%% Tanh
subplot(2,3,2)
Tanh = (exp(x)-exp(-x)).*((exp(x)+exp(-x)).^-1);
plot(x,Tanh);
title('Tanh');
latex = '$Tanh(x) = \frac{{e^x} - {e^{ - x}}}{{e^x} + {e^{ - x}}}$';
text(-9,0.6,latex,'Interpreter','latex','FontSize',11);
axis([-inf,inf,-1.05,1.05])
%% ReLU
subplot(2,3,3)
ReLU = max(0, x);
plot(x,ReLU);
title('ReLU');
latex = '$ReLU(x) = \left\{ \begin{array}{l}x,x \ge 0\\0,x < 0\end{array} \right.$';
text(-8,8,latex,'Interpreter','latex','FontSize',9);
axis([-inf,inf,-0.5,inf])
%% LeakyReLU
subplot(2,3,4)
alpha = 0.1;
LeakyReLU = max(alpha*x, x);
plot(x,LeakyReLU);
title('LeakyReLU(\alpha=0.1)');
axis([-inf,inf,-1.5,inf])
latex = '$LeakyReLU(x){\rm{ = }}\left\{ \begin{array}{l}x,x \ge 0\\\alpha x,x < 0\end{array} \right.$';
text(-9,7,latex,'Interpreter','latex','FontSize',9);
%% ELU
subplot(2,3,5)
ELU = elu(x);
plot(x,ELU);
title('ELU(\alpha=1)');
axis([-inf,inf,-1.5,inf])
latex = '$ELU = \left\{ \begin{array}{l}x,x > 0\\\alpha ({e^x} - 1),x \le 0\end{array} \right.$';
text(-8,7,latex,'Interpreter','latex','FontSize',9);
%% GELU
subplot(2,3,6)
GELU =0.5 * x .* (1 + tanh(sqrt(2/pi) * (x + 0.044715 * x.^3)));
plot(x,GELU);
title('GELU');
latex = '$GELU = x \cdot \frac{1}{2}[1 + erf(\frac{x}{{\sqrt 2 }})]$';
text(-9,7,latex,'Interpreter','latex','FontSize',10);
axis([-inf,inf,-1.5,inf])
set(0,'defaultfigurecolor','w');
sgtitle('Activation Function');
结果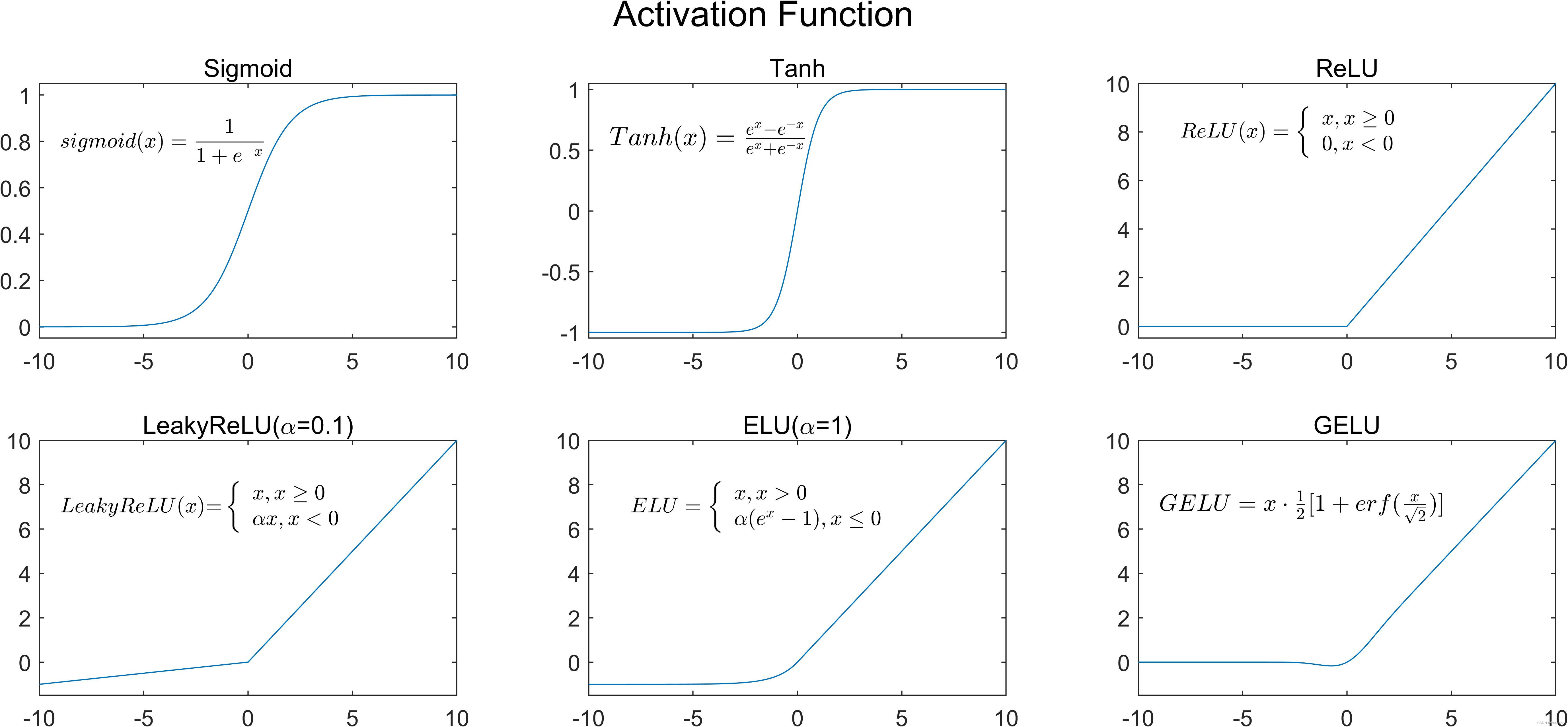




 本文展示了Sigmoid、Tanh、ReLU、LeakyReLU、ELU和GELU这六种常用的激活函数的图形表示,解释了它们的数学公式,并通过MATLAB代码进行了绘制,帮助理解这些函数在神经网络中的行为特点。
本文展示了Sigmoid、Tanh、ReLU、LeakyReLU、ELU和GELU这六种常用的激活函数的图形表示,解释了它们的数学公式,并通过MATLAB代码进行了绘制,帮助理解这些函数在神经网络中的行为特点。
















 450
450










