浮点数精度丢失

首先考虑一下下面的输出值 ，是否和你想的一样？？

 

 

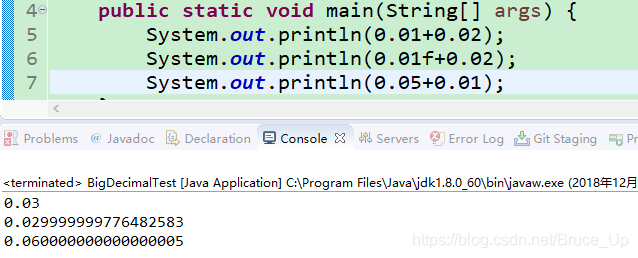
产生原因：首先计算机进行的是二进制运算，我们输入的十进制数字会先转换成二进制，进行运算后再转换为十进制输出。Float和Double提供了快速的运算，然而问题在于转换为二进制的时候，有些数字不能完全转换，只能无限接近于原本的值（类似于十进制的1/3），这就导致了在后来的运算会出现不正确结果的情况。

 

浮点运算很少是精确的，只要是超过精度能表示的范围就会产生误差。往往产生误差不是 因为数的大小，而是因为数的精度。因此，产生的结果接近但不等于想要的结果。尤其在使用 float 和 double 作精确运 算的时候要特别小心。
可以考虑采用一些替代方案来实现。如通过 String 结合 BigDecimal 或 者通过使用 long 类型来转换。

使用BigDecimal解决精度丢失问题：

BigDecimal b1 = new BigDecimal("0.05");
BigDecimal b2 = new BigDecimal("0.01");
System.out.println(b1.add(b2)); // 求和