数学模型 DAY5

最新推荐文章于 2024-08-11 02:06:50 发布

原创最新推荐文章于 2024-08-11 02:06:50 发布 · 729 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

文章介绍了层次分析法，包括一致性检验的过程和应用。接着讨论了统计模型，如线性回归、非线性模型和自回归模型，强调了残差分析在模型验证中的重要性。此外，还提到了马氏距离和两种降维方法——主成分分析及因子分析。

层次分析法

这是一个类似于神经网络的图，一层到二层，二层到三层。

先建立第二层到第三层的成对比较矩阵x1与x2重要性之比，x1与x3重要性之比等等，此时可能需要进行一致化，将各个比值转换为x1：x2：x3：...：xn，直接提取这里的取值就好，就可以一致化。得到的矩阵称为n阶一致阵A

Aw= $\AA$ w，w为权向量， $\AA$ 为A的最大特征根，通过Matlab可以算出 $\AA$ 和w。

一致性指标和一致性检验

$CI=\frac{\lambda -n}{n-1}$

CI为一致性指标，CI=0时，A为一致阵，CI越大，A越不一致，

随机一致性指标，有一个随机一致性指标RI，可以上网搜这个表

RI随着A的阶数n改变而改变

得到CI和RI后，计算比值CR，并且当CR满足这个条件的时候

$CR=\frac{CI}{RI}<0.1$

A的不一致程度在容许范围之内，0.1是可以调整的，对于重要决策的问题应该适当减小

上述过程为一致性检验，若检验通过，则可以用A的特征向量作为权向量。

A一致性检验通过后，开始做综合权重，先做第二层对第一层目标的权重，得到四个成比较矩阵，依次为B1,B2,B3,B4

由Bj可以计算每个矩阵的最大特征根，，最终得到的一个特征矩阵wj，为第三层对第二层的权重。

最后通过公式， $\omega ^3=\left[ \omega _1,\omega _2,\omega _3,\omega _4 \right]$

$W=\omega ^3w^2$

最终得到的W，为第三层对第一层的特征矩阵，也就是第三层对第一层的权值

通过这个权重，可以知道Xi对Y的重要性

比较尺度，也就是xi对xj重要性比较时的取值标志

最终利用第二层对第一层的权值，分别乘以第三层在第二层的分数，最终得到一个最终的得分。

统计模型

统计模型包含各种回归，线性回归，非线性回归，自回归，logit回归，判别分析模型

线性回归，又有一元和多元，一元是只和一个自变量因素有关，多元是和多个因素有关。

在建立方程的时候，形式如下 y=b0+b1x+e

b0 b1可通过编程求解，e表示随机误差，除了方程内自变量之外的所有影响y的随机因素的总和。

编程输出结果还有R-square F p s-square

R方代表拟合系数，R方越大，残差平方和越小，拟合效果越好

F代表拟合显著性，F越大越好，它综合考虑了召回率和精确率

p值是用来判断拒绝域的，首先有个α，一般α=0.05，代表有0.05在拒绝域内，而p一般要小于α。

置信水平为1-α，置信区间代表这个回归系数最大最小可以取到什么值

s方代表方差，方差越大，模型越不稳定，s方越小越好

残差代表y的实际值与预测值之差，市委随机误差e的估计值。无论是残差还是回归系数的置信区间都不可以含有零点。若残差的置信区间内含有零点，可以认为这些数据偏离整体数据的变化趋势，称为异常点，应予以剔除。

多元线性回归也只是多个自变量的回归而已，只是可以通过判断模型是否受到两个或以上因素的综合影响，可以设置一个自变量为x1*x2

但是不可能把所有因素都归到回归方程内，因此有逐步回归这个方法

逐步回归分析是在回归分析的基础上，加入了一项功能，即自动化移除掉不显著的X，其结果各指标意义与回归分析均一致。

在多元线性回归中，要注意因素与因素之间的关联性，可以先直接把各个因素加进来，然后利用编程计算得到输出结果，看看输出结果是否合适，各项评价指标是否都较为不错。

如果评价指标有了问题，这个时候可以使用残差分析法，建立残差与不同自变量的散点图，观察是否有一定的关联，尝试把一些因素综合起来考虑，建立不同的多元线性回归方程，并且观察残差图以及各项评价指标的变化。

残差分析图标准，没有异常点，要么不随自变量变化，趋于平稳，要么就体现不可预测性与随机性，足够乱。

非线性模型，一般可以上网去搜索相关领域的模型，然后再去考虑一些其他因素去优化拟合效果。

在进行回归方程的建立时，可以先去将因变量与各个自变量的散点图做出来，看看线性关系之类的

自回归模型，当引入了时间序列时，模型也许单纯通过多元线性回归已经可以拟合的较为成功了，但是在对时间序列分析时，模型的随机误差e，有可能存在相关性，违背模型关于随机误差e对其余因素都相互独立的基本假设，因此，随机误差e此时会显示自相关性，此模型不可用

为了检查自相关性，需要利用到残差分析法，首先将所有残差进行求解，建立ei-ei-1残差图，如果有一定趋势，则确实随机误差e与时序关系有一定关联，有自相关性。

因此此时多元线性方程建立应为：

$y_t=\beta _0+\beta _1x_{1t}+\beta _2x_{2t}+\varepsilon _t$

$\varepsilon _t=\rho \varepsilon _{t-1}+\mu _t$

$\rho$ 为自相关系数

DW检验，这是一种常用的诊断自相关现象的统计方法

$DW=\frac{\sum_{t=2}^n{\left( e_t-e_{t-1} \right) ^2}}{\sum_{t=2}^n{e_t^2}}$

通过DW值可以估算 $\rho$ ，查DW分布表，得到检验的临界值dL和dU，最后由DW所在区间决定

若 0<D.W.<dL 存在正自相关
dL<D.W.<dU 不能确定
dU <D.W.<4－dU 无自相关
4－dU <D.W.<4－ dL 不能确定
4－dL <D.W.<4 存在负自相关

算出DW值后，可以算出 $\rho$ ，然后做广义差分变换，最后得到

$y_t^*=y_t-\rho y_{t-1}\ x_{it}^*=x_t-\rho x_{i,t-1}$

$y_t^*=\beta _0^*+\beta _1x_{1t}^*+\beta _2x_{2t}^*+\mu _t$

$\beta _0^*=\beta _0\left( 1-\rho \right)$

最后利用这个回归方程得到回归系数的解，在把原始变量回代回去方程，得到最后的回归方程，可以做图，预测，计算残差，看看模型的好坏。

logit回归模型，先对数据进行一些处理之后，绘制散点图，观察走势，若呈现S型（类似于环境容纳量走势）则可以用logit模型。公式如下

$\ln \frac{p}{1-p}=\beta _0+\beta _1x_1+\beta _2x_2+...+\beta _nx_n$

其中p为事件发生概率，1-p为事件不发生概率

处理此类问题的另一个模型为probit模型，其形式为

$p=\phi \left( \beta _0+\beta _1x \right)$

$probit\left( p \right) =\phi ^{-1}\left( p \right) =\beta _0+\beta _1x$

遇到此类问题，可以同时建立这两种模型，并进行模型比较

马氏距离与欧氏距离

马氏距离公式：

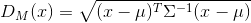
对比欧氏距离，他还考虑了变量之间的相关性，因此乘以了协方差矩阵的逆矩阵

主成分分析

首先有个p维的随机变量，假设x的期望向量为u，协方差矩阵为Cov(x)，用一组向量a1,a2,a3,...,ap构造x的p个线性组合，称为主成分y=(y1,y2,y3,...,yp)T

$y_1=a_{11}x_1+a_{12}x_2+...+a_{1p}x_p=\boldsymbol{a}_1^{\boldsymbol{T}}\boldsymbol{x}$

$y_2=a_{21}x_1+a_{22}x_2+...+a_{2p}x_p=\boldsymbol{a}_2^{\boldsymbol{T}}\boldsymbol{x}$

$......$

$y_p=a_{p1}x_1+a_{p2}x_2+...+a_{pp}x_{p}=\boldsymbol{a}_{\boldsymbol{p}}^{\boldsymbol{T}}\boldsymbol{x}$

a1,a2,...,ap为主成分载荷系数，后面通过编程计算，得出协方差矩阵的特征根，计算每一个特征根的方差贡献率，当方差累计贡献率超过80%时，即可确定，有几个主成分，通过输出的主成分系数矩阵，可以得到第一个和第二个主成分的方程，通过不同主成分的各自的主成分的系数，分析每个主成分的含义到底是什么，最后得到每个主成分的得分，对变量进行分析。