在上篇文章了解了堆的基本功能后,我们便可以使用堆来实现其独特的功能——堆排序与Top-K问题,我们一起来往下学习。
目录
一、 堆排序(test)的打印
基于上篇文章的学习,我们发现,如果是小堆,那堆顶的数据一定是最小的,那这样我们就可以每次打印出堆顶的元素,然后弹出堆顶的元素(最小的元素),一直保持堆顶的元素是堆中最小的,这样,就可以将堆中的数据从小到大排序。
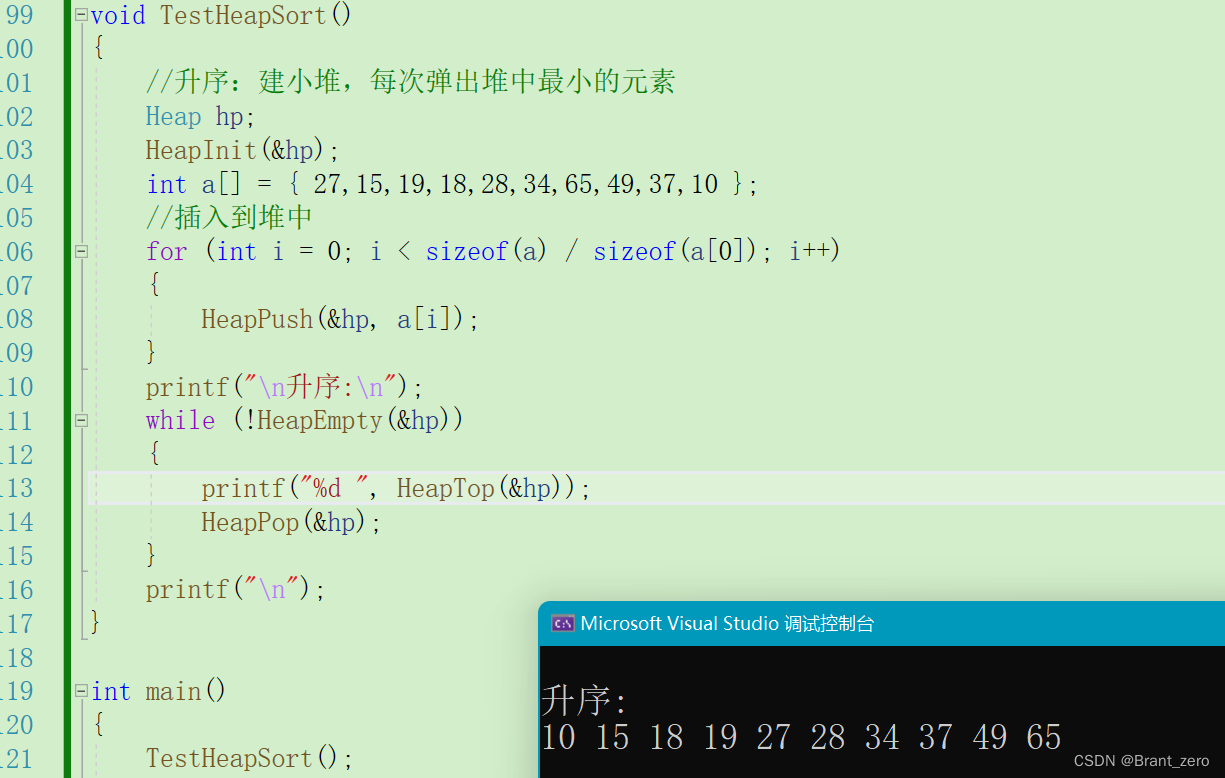
这样就可以将一个数组中的元素进行排序。
不难发现,我们这样排序的空间复杂度:O(N),时间复杂度:O(N*logN)。
但是我们一般排序都是将数组中的元素进行排序,而不是将其打印出来,接下来我们看看如何将数组中的值排序吧。
二、 堆排序的插入
思想:
①以建小堆的方式,将数组中的值不断放入到堆中(建堆)。
②然后将堆顶的元素放回到数组中,然后弹出堆顶元素,直到堆为空,这样数组中就的值就有序了。
void HeapSortInsert(int* a, int n)
{
//升序:建小堆,每次弹出堆中最小的元素
Heap hp;
HeapInit(&hp);
// 将传入的a数组中的值,插入到堆中
for (int i = 0; i < n; i++)
{
HeapPush(&hp, a[i]);
}
int i = 0;
printf("\n升序:\n");
//再将堆顶的数据依次插入到数组中 直到堆为空
while (!HeapEmpty(&hp))
{
a[i++] = HeapTop(&hp);
HeapPop(&hp);
}
printf("\n");
}我们来看看排序之后的结果。
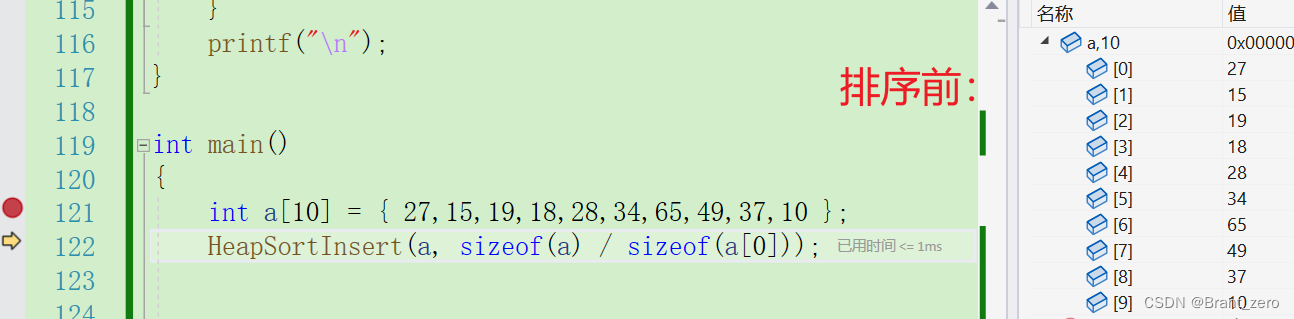
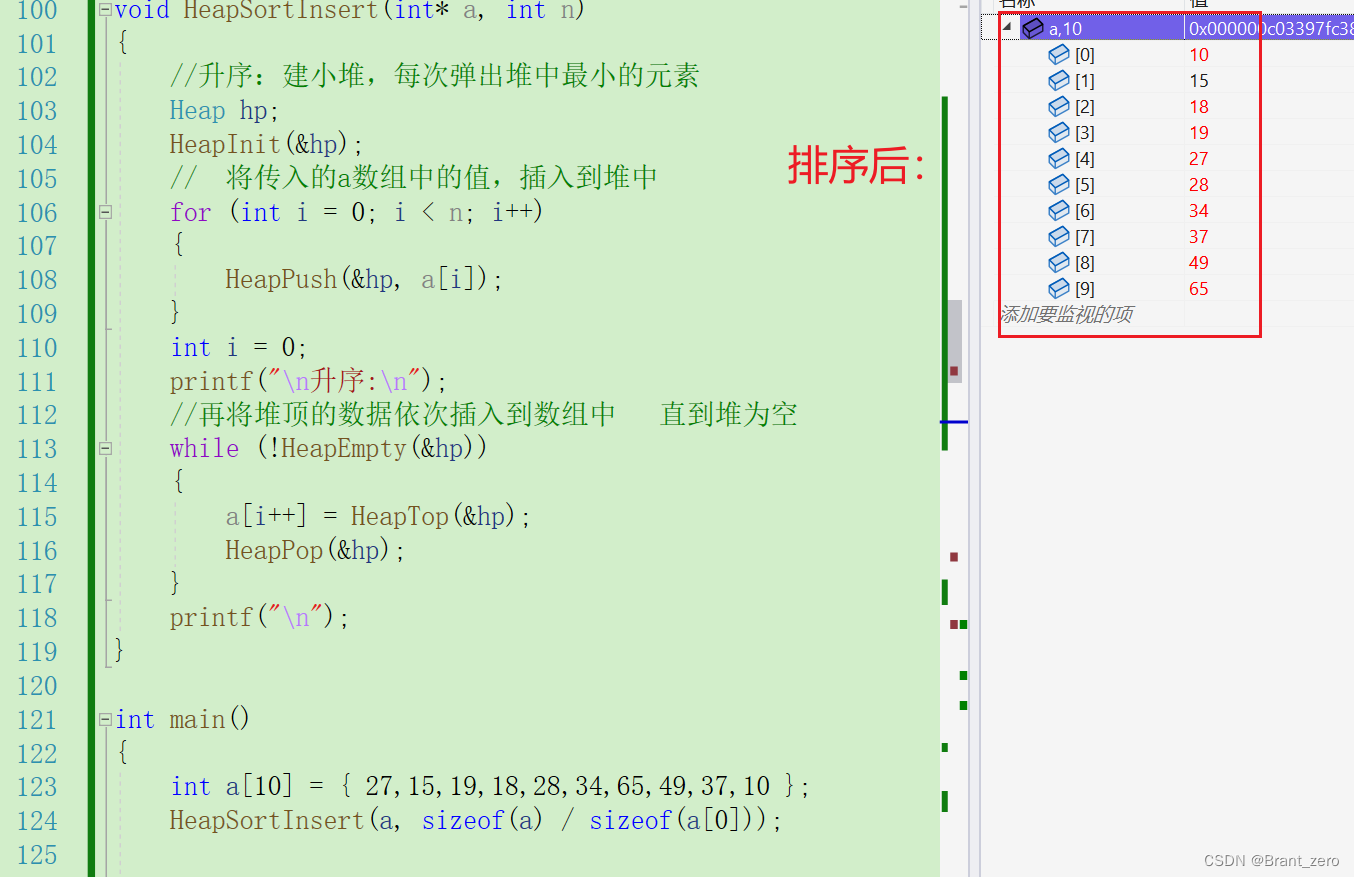
不难发现,使用了HeapSortInsert堆排序后,数组中的元素就被排好了序。
可是此时面临两个问题:
问题1:首先要写一个堆数据结构,将问题复杂化了。
问题2:虽然时间复杂度达到了O(N * lonN),但有O(N)的空间复杂度。
这样的堆排序完全没有展现出它结构优势,所以接下来我们要实现真正的堆排序,不用额外创建一个堆的数据结构,并且空间复杂度达到O(1);
三、 堆排序
接下来算是真正的进入正题,如何实现堆排序。
3.1 堆排序的实现
思路:
①以升序为例,在原数组上建立一个大堆。
②从最后一个非叶子结点开始,使用向下调整算法开始建立大堆。
③因为堆顶元素最大,所以不断把堆顶元素放入数组末尾(即将大的沉到堆底,具体请看下面的GIF图),然后将新堆顶的数据进行向下调整,使其稳定堆的结构,直到n个数调整完成。
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >=0 ; i--)
{
//n是数组大小,数组大小即sizeof(a)的大小,数组操作实际是从下标开始操作
AdjuestDown(a, n, i);
}
int end = n - 1;
while (end>0)
{
swap(&a[0], &a[end]); //将最大的沉到堆底.
AdjuestDown(a, end, 0);
end--;
}
}3.2 堆排序的过程
我们排序这个数组来举例堆排序的实现
int main ()
{
int a[] = { 65,17,9,53,45,23,78 };
HeapSort(a, sizeof(a) / sizeof(a[0]));
Print(a, sizeof(a) / sizeof(a[0]));
return 0;
}
接下来我们来看看堆排序是如何将大堆的结构进而转化为升序的。
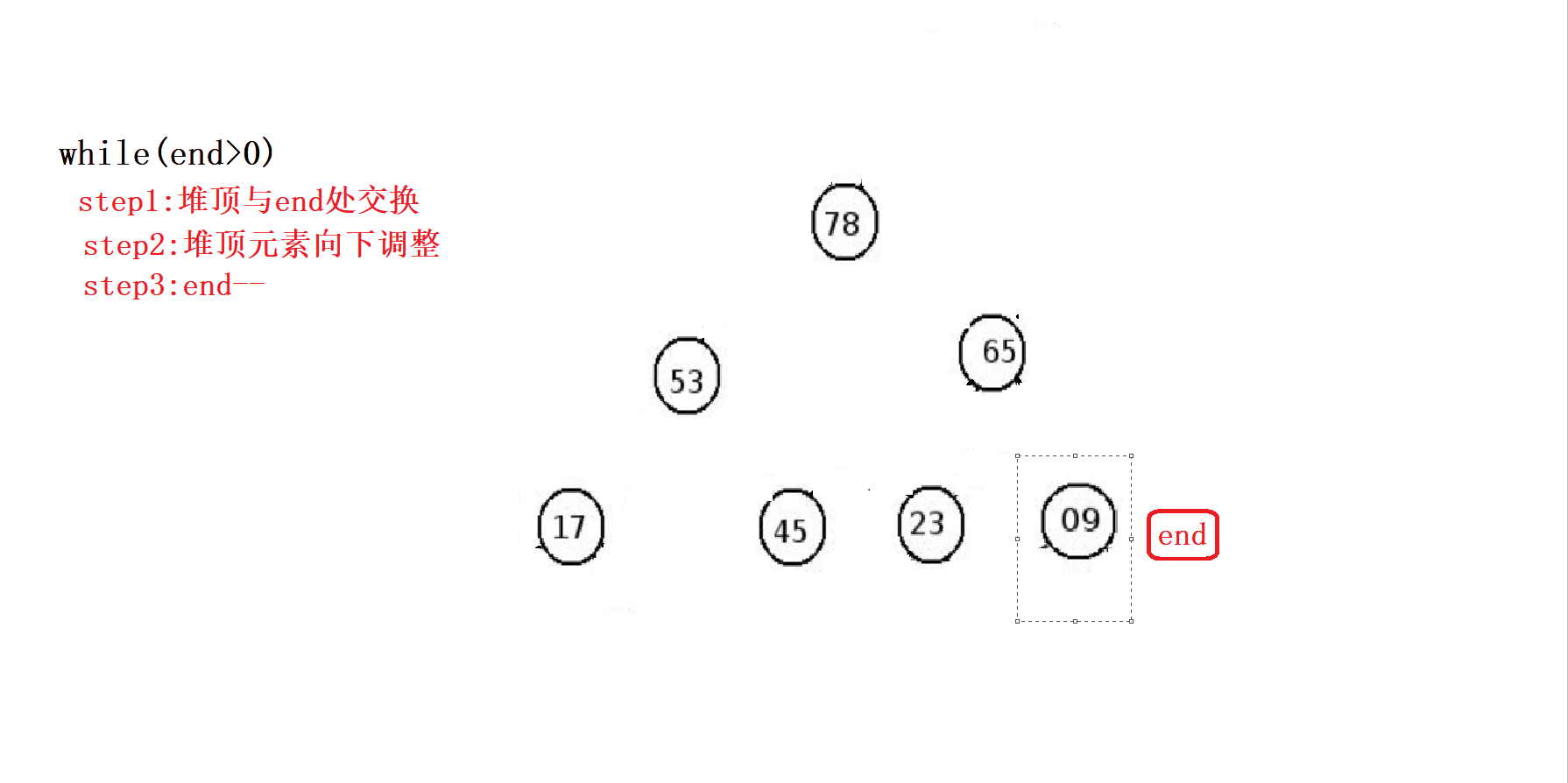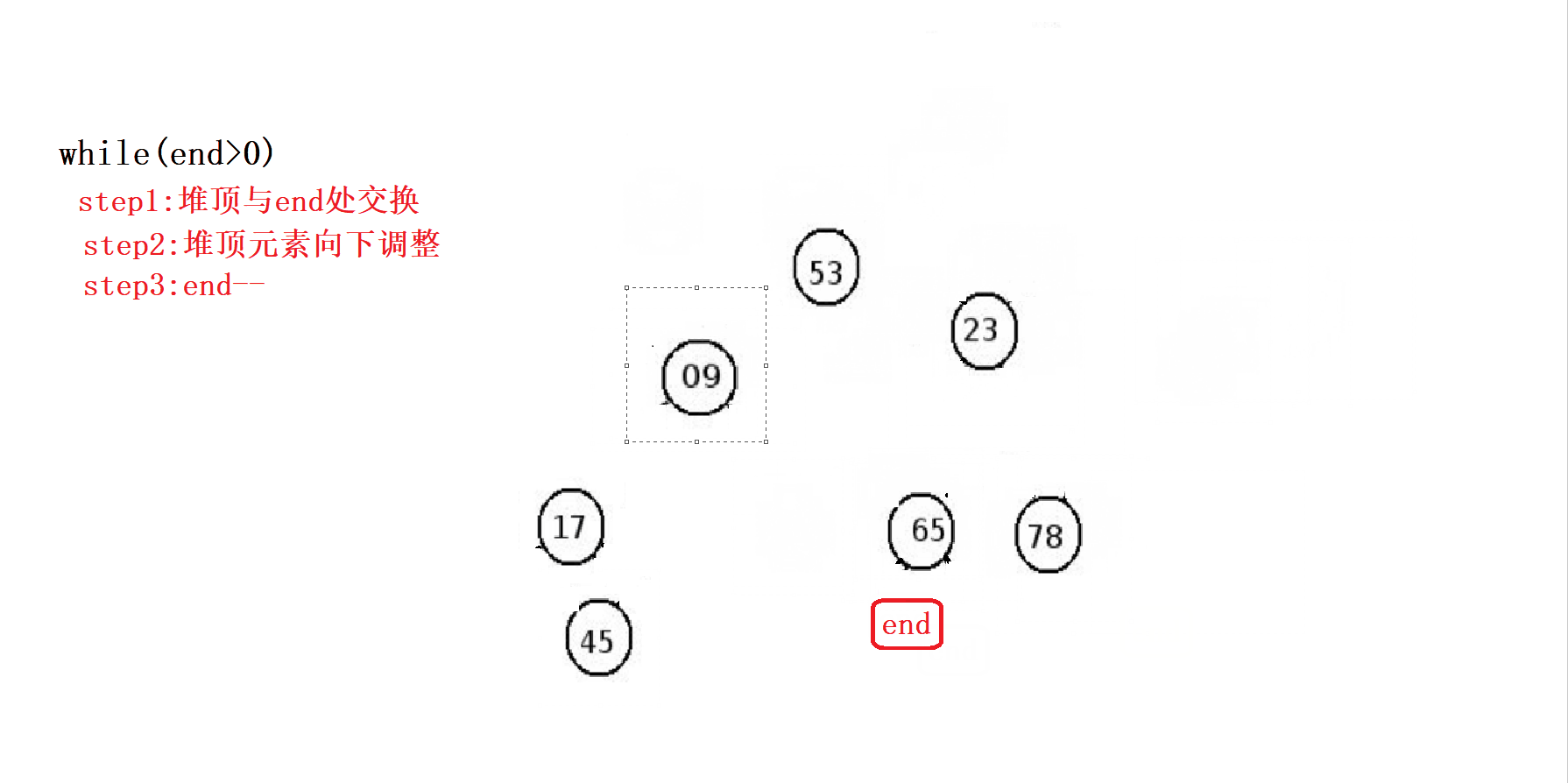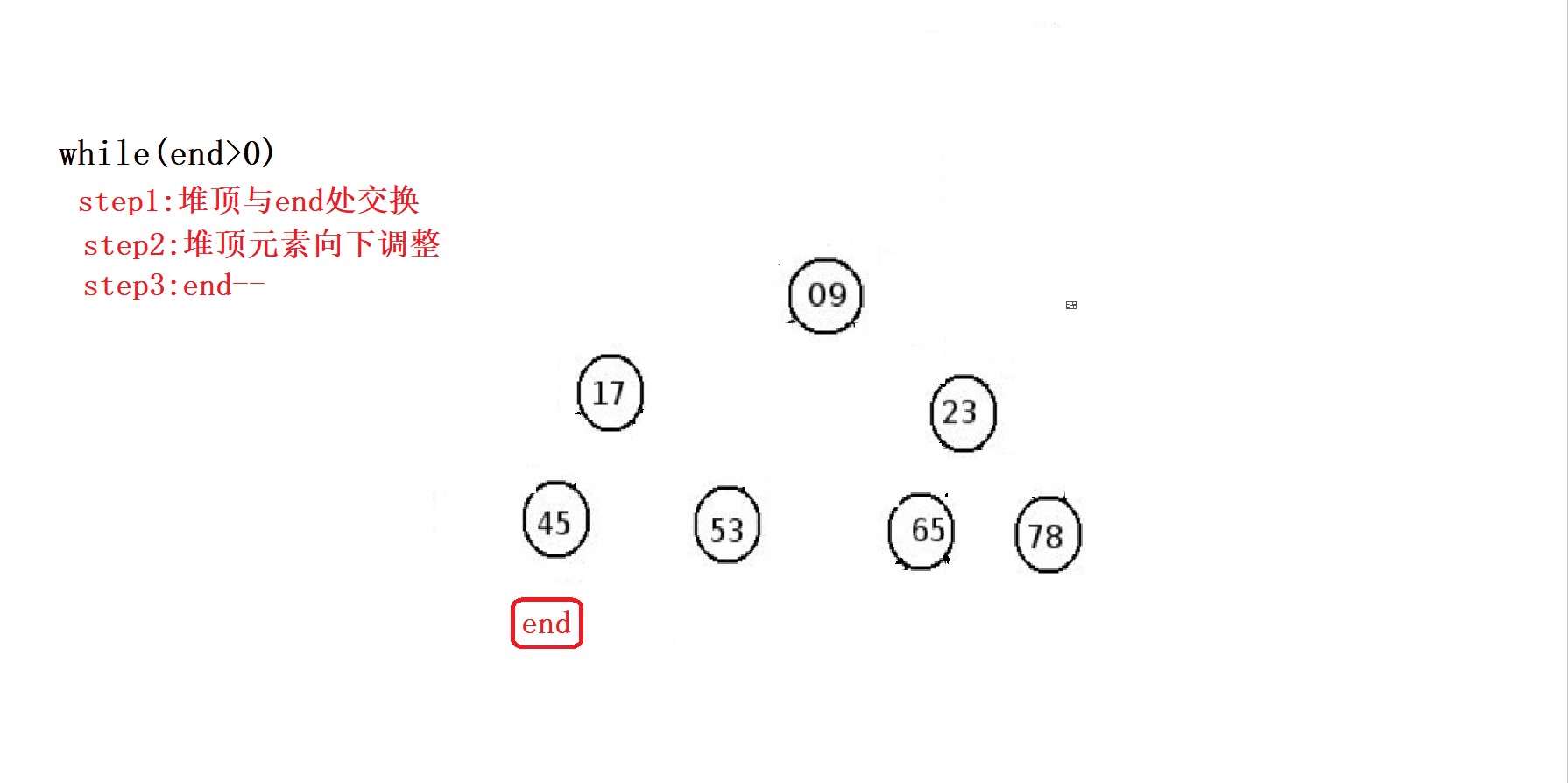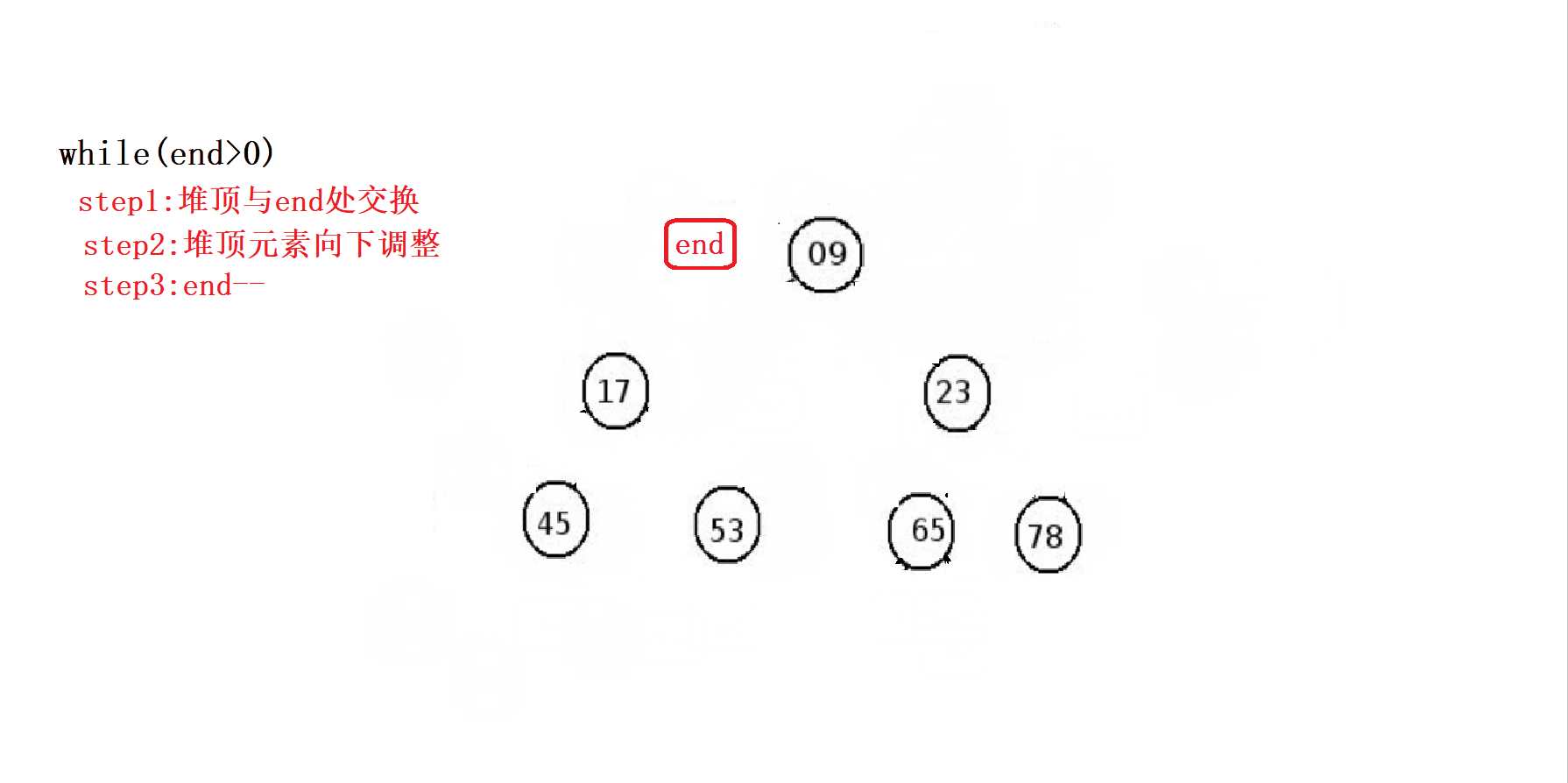
排完之后,我们将其输出:

这时,堆排序就实现了,此时,不管是时间复杂度O(N*logN),还是空间复杂度O(1)都达到了极限。
并且堆排序的只需要一个向下调整算法即可(AdjustDown),实现起来也没那么复杂了。
3.3 堆排序的注意事项
这里有四个注意的点:
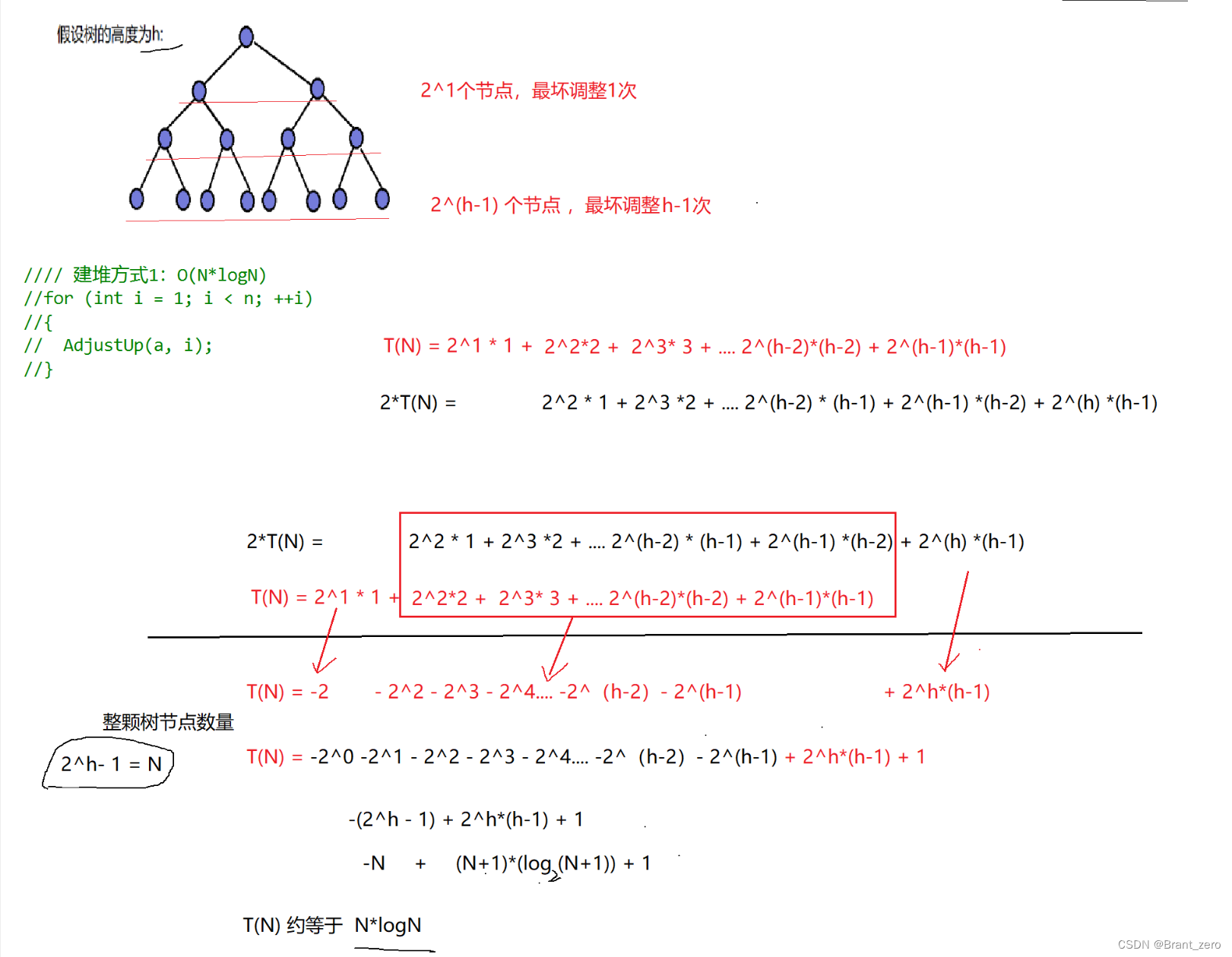
①实现堆排序必须先完成建堆的过程,堆排序的建堆是在数组自身中建队,而在建堆过程中我们使用向下建堆的时间复杂度是O(N),向上调整建堆的空间复杂度是0(N*logN),具体推导过程我放在下面。
②向下调整建堆要从倒数第一个非叶子节点开始调整。即从最后一个节点的父亲开始调整。
计算那个结点的方式是:n-1是算出最后一个节点的下标,然后套规律 父亲=(孩子-1)/2。 所以是(n-1-1) /2 。
③调用向下调整时的注意点:我们使用end表示堆未排序的最后一个元素的下标,在我们进行向下调整时,传入的调整数组大小是end,传入end+1则是整个数组。因为我们不想让刚下来的堆顶元素被调换,其下标是end,所以传入数组大小为end,最多调换到end-1下标处的元素,正好避免此元素被调整。
④要控制调整的次数。即while的条件是(end>0),在end == 0时结束调整,因为当end为1时,end与堆顶元素即a[0]调整,如果不控制end == 0则会出现自己与自己调换,很明显这是不符合的。
3.4 向下调整建堆的效率
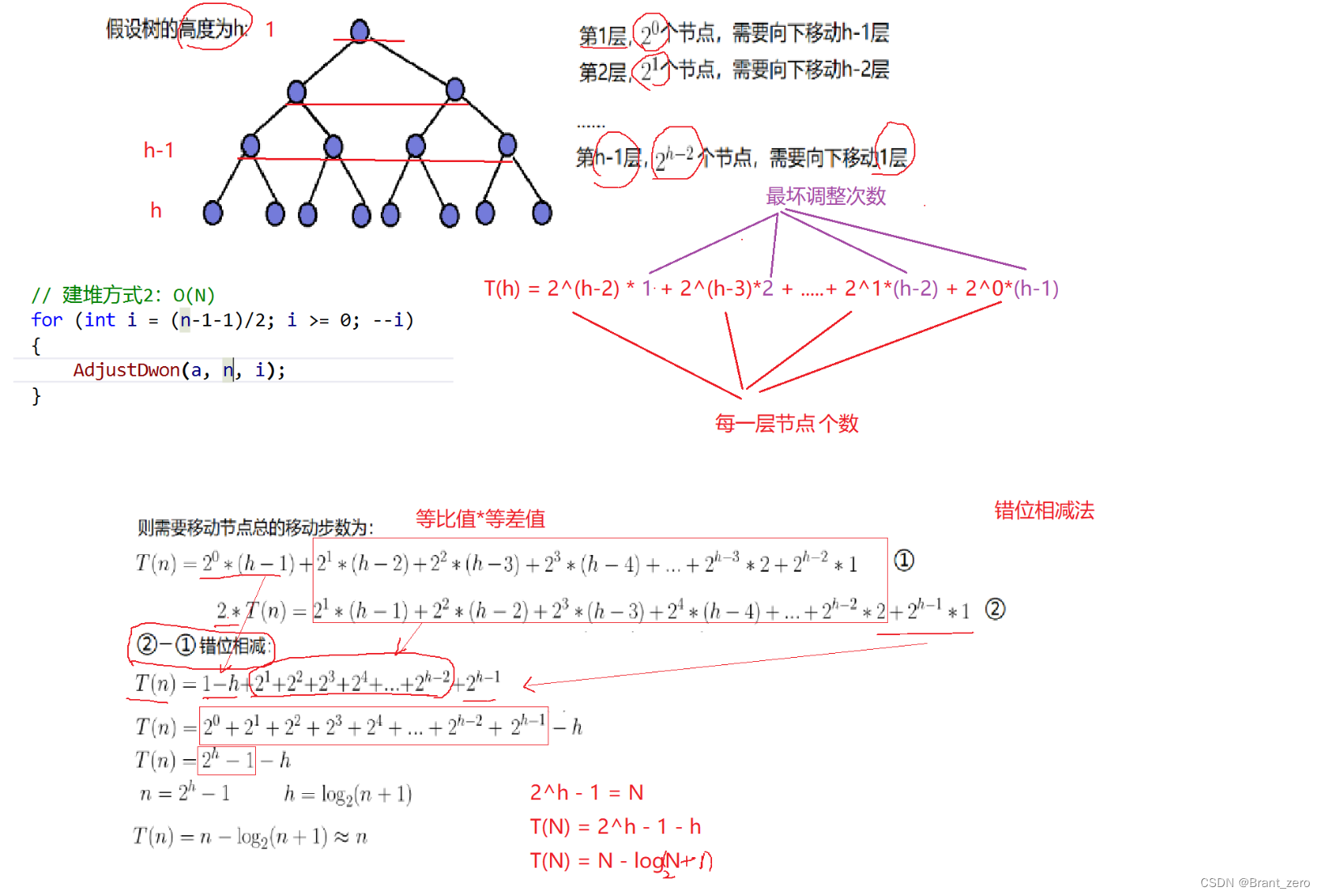
3.5 向上调整建堆的效率
四、 Top-K问题
4.1 Top-K问题是什么
Top-K问题:即求数据结合中前K个最大元素或最小的元素,一般情况下数据量比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100名活跃玩家
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可行了(数据量太大无法全部加载到内存中),这时最佳的解决方案就是使用堆来解决。
4.2 Top-K的实现
思路如下:
①用数据集合中前K个元素来建堆
前k个最大的元素,建小堆
前k个最小的元素,建大堆
②用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或最大的元素。
//求n个数中的前k的数,建小堆。
void PrintTopK(int* a, int n, int k) {
// 一、 建堆--用a中前k个元素建堆
//先建立一个k个数的数组,有时可能会要求返回此数组,所以要使用malloc开辟数组。
int* KMinHeap = (int*)malloc(sizeof(int) * k);
assert(KMinHeap);
//将k个元素先直接放入到数组中
for (int i = 0; i < k; ++i)
{
KMinHeap[i] = a[i];
}
//使用向下建堆的方式构建堆 -- 类似堆排序的建堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjuestDown(KMinHeap, k, i);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
for (int j = k; j < n; ++j)
{
if (a[j] > KMinHeap[0])
{
KMinHeap[0] = a[j];
AdjuestDown(KMinHeap, k, 0);
}
}
//打印堆中的数据
for (int i = 0; i < k; ++i)
{
printf("%d ", KMinHeap[i]);
}
}以上是以减小堆来举例,同样有几个注意的点。
1. 开始是直接将k个数放入到Top-k数组中,好比是创建了一个数组,然后使用向下调整,将其变为了小堆。
2.最大的K的数,应建小堆,因为此时堆顶的数据是Top-k数组中最小的,我们拿剩下的n-k个数与堆顶数据比较。如果出现比堆顶数据大的,则要放入堆,说明这个数是前K个,再向下调整到合适的位置。一直循环,直到遍历完这个数据集合。
4.3 检测Top-k
思路:
创建一个1000个数的数据集合,其中每个数都小于1w,然后让10个数大于1w,将这个数据集合传入函数中,让其打印出这10个元素,即可检测我们实现的Top-K是否有问题。
测试代码:
void TestTopk()
{
int n = 1000;
int* a = (int*)malloc(sizeof(int) * n);
srand((unsigned int)time(NULL));
for (int i = 0; i < n; ++i)
{
//所有数取模上10000,就导致生成的数不可能超过10000,
a[i] = rand() % 10000;
}
//将其中几个数设置为1w以上。
a[5] = 10000 + 1;
a[121] = 10000 + 2;
a[531] = 10000 + 3;
a[511] = 10000 + 4;
a[115] = 10000 + 5;
a[335] = 10000 + 6;
a[999] = 10000 + 7;
a[76] = 10000 + 8;
a[423] = 10000 + 9;
a[314] = 10000 + 10;
PrintTopK(a, n, 10);
}结果如下:
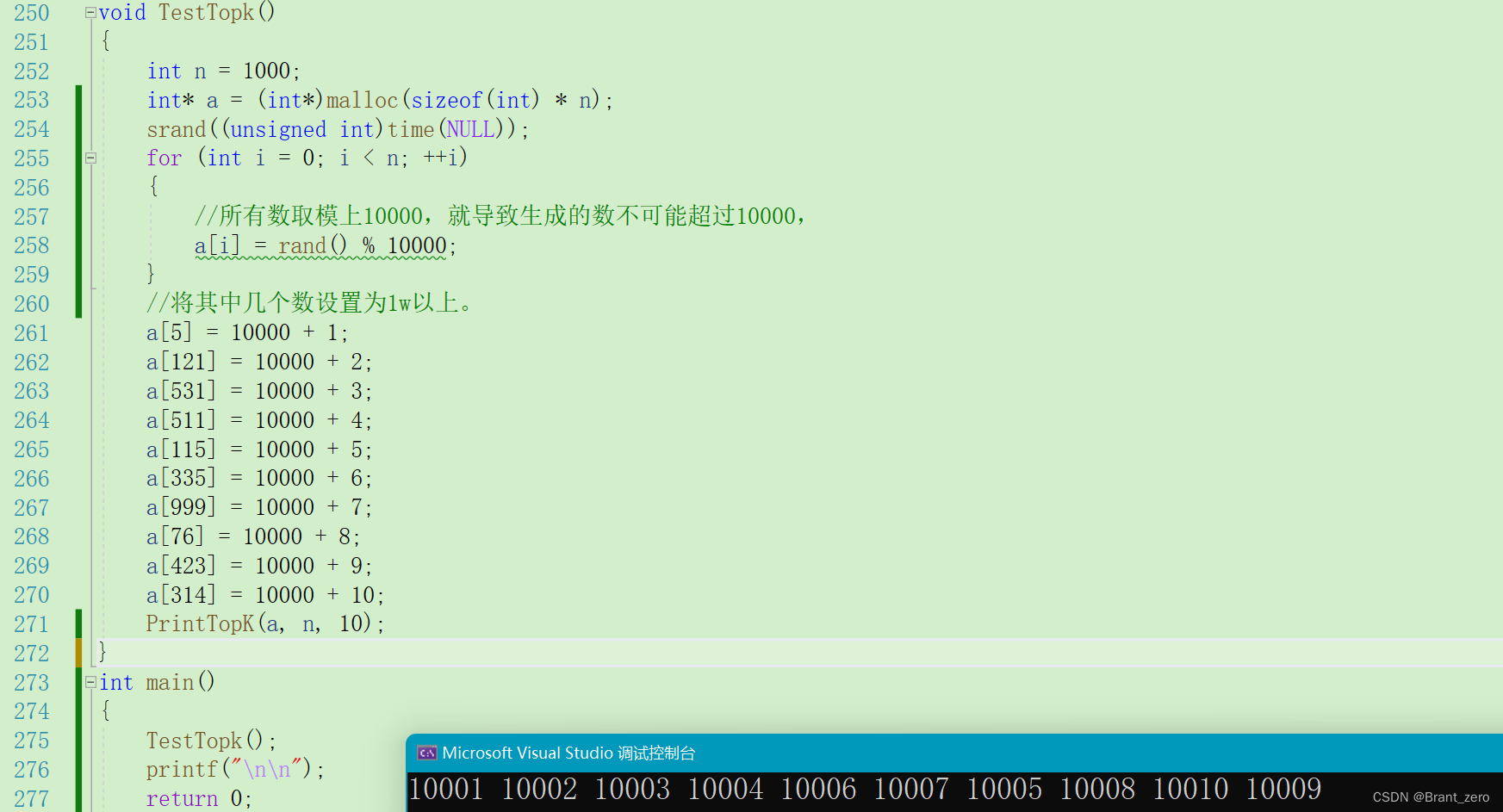
这样Top-K问题就实现了,时间复杂度为O(K+(N-K)*logK),空间复杂度为O(K),这是实现Top-k问题时间、空间效率都非常高的一种方法。
五、 总结部分
本篇博客实现了堆排序,一步一步优化推出堆排序,并且巧妙的解决了Top-K问题。其中有一些难得理解的地方。
比如升序应该建立什么堆,为什么升序要建立大堆,然后对这个是大堆如何操作将其变成有序序列的。
再如为什么要使用向下调整而不使用向上调整算法,以及向下调整算法为什么比向上调整算法的时间复杂度低;还有怎么实现向下调整,向下调整是从哪个结点开始调整的,如何计算那个结点;这些是堆排序需要重点理解的点。
然后是Top-K问题中取前k个数要建立什么堆,为什么要这样建立,建立完之后剩下n-k的数需要做什么,每次比较之后为什么还要进行调整,这些则是Top-K问题需要重点理解的点。
本篇内容需要一定的理解,开始可能会比较抽象,多去画图实践结合调试去观测,就会发现其规律,理解之后就会领悟其中的奥妙。
好了,本篇文章就结束了,堆的相关内容也就告一段落了,接下来会进入其他的排序的学习中,希望大家持续关注,我们下期再见。
点点关注点点赞呗,谢谢~~







 本文深入探讨了堆排序的实现过程,包括建堆、堆排序的步骤及注意事项,详细解析了向下调整建堆的效率。同时,介绍了如何利用堆解决Top-K问题,通过建立小堆找到数据集中的前K个最小元素。最后,通过实例展示了堆排序和Top-K问题的解决方案及其优化。
本文深入探讨了堆排序的实现过程,包括建堆、堆排序的步骤及注意事项,详细解析了向下调整建堆的效率。同时,介绍了如何利用堆解决Top-K问题,通过建立小堆找到数据集中的前K个最小元素。最后,通过实例展示了堆排序和Top-K问题的解决方案及其优化。

















 8986
8986

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










