排序(Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个关键字有序的序列。
稳定度(稳定性)一个排序算法是稳定的,就是当有两个相等记录的关键字R和S,且在原本的列表中R出现在S之前,在排序过的列表中R也将会是在S之前。
例如,一组数排序前是a1, a2, a3, a4, a5,其中a2=a4,经过某种排序后为a1, a2, a4, a3, a5,则说这种排序是稳定的,因为a2排序在a4的前边,排序后它还是在a4的前边,假如变成了a1, a4, a2, a3, a5就是不稳定的了。
稳定的排序算法有直接插入排序、冒泡排序和归并排序,
不稳定的排序算法有希尔排序、快速排序、简单选择排序和堆排序。
不稳定排序算法可能会在相等的键值中改变纪录的相对次序,但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩充键值的比较,如此在其他方面相同键值的两个对象间之比较,就会被决定使用在原先数据次序中的条目,当作一个同分决赛。然而,要记住这种次序通常牵涉到额外的空间负担。
在计算机科学所使用的排序算法通常被分类为:
- 计算的复杂度(最差、平均、和最好性能),依据列表(list)的大小(n)。 一般而言,好的性能是 O(nlogn),且坏的性能是 O(n^2)。对于一个排序理想的性能是 O(n)。 而仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要 O(nlogn)。
- 存储器使用量(空间复杂度)(以及其他电脑资源的使用)
- 稳定度:稳定的排序算法会依照相等的关键(换言之就是值)维持纪录的相对次序。
- 一般的方法:插入、交换、选择、合并等等。交换排序包含冒泡排序和快速排序。插入排序包含希尔排序,选择排序包括堆排序等。
排序算法比较表
| 算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 稳定性 | 备注 |
|---|---|---|---|---|---|---|
| 选择排序 | O ( N 2 ) O(N^2) O(N2) | O ( N 2 ) O(N^2) O(N2) | O ( N 2 ) O(N^2) O(N2) | O ( 1 ) O(1) O(1) | 不稳定 | N小时好 |
| 插入排序 | O ( N 2 ) O(N^2) O(N2) | O ( N ) O(N) O(N) | O ( N 2 ) O(N^2) O(N2) | O ( 1 ) O(1) O(1) | 稳定 | 大部分有序时好 |
| 冒泡排序 | O ( N 2 ) O(N^2) O(N2) | O ( N ) O(N) O(N) | O ( N 2 ) O(N^2) O(N2) | O ( 1 ) O(1) O(1) | 稳定 | N小时好 |
| 希尔排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N ) O(N) O(N) | O ( N s ) 1 < s < 2 O(N^s) 1<s<2 O(Ns)1<s<2 | O ( 1 ) O(1) O(1) | 不稳定 | s是所选分组 |
| 快速排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N 2 ) O(N^2) O(N2) | O ( l o g N ) O(logN) O(logN) | 不稳定 | N大时好 |
| 堆排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N l o g N ) O(NlogN) O(NlogN) | O ( 1 ) O(1) O(1) | 不稳定 | N大时好 |
| 归并排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N ) O(N) O(N) | 稳定 | N大时好 |
1.选择排序
给定一组数据,经过第一轮比较后找出最小值与第一个记录交换,第二轮找到除第一个的最小值之后与第二个记录交换,每次都找到剩余数的最小值之后与第n-1个数交换,如第五轮就与第4个数交换。

使用选择排序为一列数字进行排序的过程(图片来源维基百科)
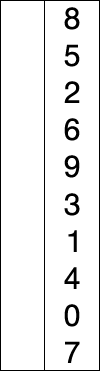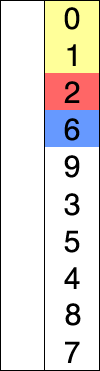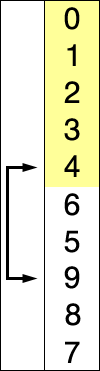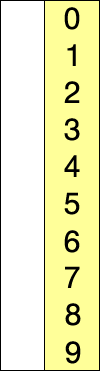
选择排序的示例动画(红色表示当前最小值,黄色表示已排序序列,蓝色表示当前位置)
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
/*
//模板函数的使用,这样的话什么类型的数据进来都可以作比较
template <typename T>
void Selectsort(vector<T> &nums){
*/
void Selectsort(vector<int> &nums){
//与上边注释段可做替换
int len=nums.size();
for (int i=0;i<len;i++)
{
int min_num=i;
for (int j=i;j<len;j++)
{
if (nums[j]<nums[min_num]) min_num=j;
}
if(min_num!=i) swap(nums[i],nums[min_num]);
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[10]={10,9,8,7,6,5,4,3,2,1};
vector<int> nums(a,a+10);
Selectsort(nums);
for (int i=0;i<nums.size();i++)
cout<<nums[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:
2.插入排序
给定一组数据,初始时假设第一个数据自成一个有序数列,其余的数据为无序数列;接着从第二个数据开始,按照记录的大小依次将当前数据插入到之前的有序序列中,直至最后一个数据插入到有序数列终止。

使用插入排序为一列数字进行排序的过程(图片来源维基百科)

插入排序的示例动画
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
/*
template <typename T> //定义T参数类型,根据传入的数据类型确定
{//插入排序
int numlen=numbers.size();
int flag;
T temp;
for (int i=1;i<numlen;i++)
{
temp=numbers[i];
for (flag=i;flag>0&&numbers[flag-1] > temp;flag--)
numbers[flag]=numbers[flag-1];
numbers[flag] = temp;
}
}
*/
//上边注释的函数与下边两个函数加起来的作用相同,可以替换
void insertsort(vector<int> &numbers){
int numlen=numbers.size();
int flag;
int temp;
for (int i=1;i<numlen;i++){
temp=numbers[i];
for (flag=i;flag>0&&numbers[flag-1] > temp;flag--)
numbers[flag]=numbers[flag-1];
numbers[flag] = temp;
}
}
void insertsort(vector<char> &numbers){
int numlen=numbers.size();
int flag;
char temp;
for (int i=1;i<numlen;i++){
temp=numbers[i];
for (flag=i;flag>0&&numbers[flag-1] > temp;flag--)
numbers[flag]=numbers[flag-1];
numbers[flag] = temp;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[]={9,8,7,6,5,4,3,2,1};
char b[]={'j','f','e','d','c','b','a'};
vector<int> numbers(a,a+9);
vector<char> character(b,b+7);
insertsort(numbers);
insertsort(character);
for (int i=0;i<numbers.size();i++)
cout<<numbers[i]<<" ";
cout<<endl;
for (int i=0;i<character.size();i++)
cout<<character[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:
3.冒泡排序
单向冒泡排序的基本思想是,对于给定的n个数据,从第一个数据开始依次对相邻的两个记录进行比较,当前面记录大于后面记录时交换其位置,一轮比较完后n个记录中的最大记录将位于第n位,然后对前n-1个数据进行第二轮比较;重复该过程直到进行比较的数据只剩下一个为止。
笔者稍稍做了改进,增加一个bool型变量,当一轮比较没有交换数据时说明这组数据已经有序,可以中断直接返回该组数据。

使用冒泡排序为一列数字进行排序的过程(图片来源维基百科)
冒泡排序的示例动画
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
//这里我直接用模板函数,如有不懂请看我写的另一篇帖子--两步学会C++模板的使用<1>
template <typename T> //定义Tx参数类型,根据传入的数据类型确定
void Bubblesort(vector<T> &numbers){//冒泡排序
int numlen=numbers.size();
bool flag;
for (int i=numlen-1;i>=0;i--){
flag=true;
for (int j=1;j<=i;j++){
if(numbers[j]<numbers[j-1]){
swap(numbers[j],numbers[j-1]);
flag=false;
}
}
if(flag) break;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[]={9,8,7,6,5,4,3,2,1};
char b[]={'j','f','e','d','c','b','a'};
vector<int> numbers(a,a+9);
vector<char> character(b,b+7);
Bubblesort(numbers);
Bubblesort(character);
for (int i=0;i<numbers.size();i++)
cout<<numbers[i]<<" ";
cout<<endl;
for (int i=0;i<character.size();i++)
cout<<character[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:
4.希尔排序
希尔排序也称“缩小增量排序”。它的基本原理是:首先将待排序的元素分为多个子序列,使得每个子序列的元素个数相对较少,对各个子序列进行直接插入排序,待整个待排序列基本有序后,再对所有元素进行一次直接插入排序。
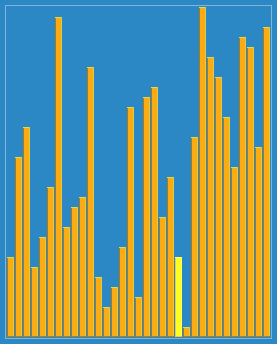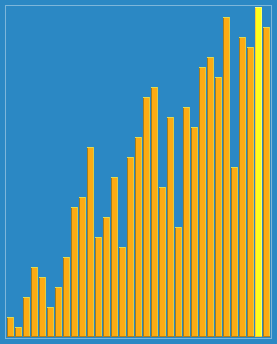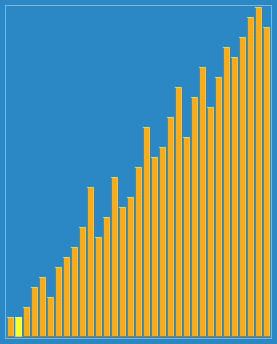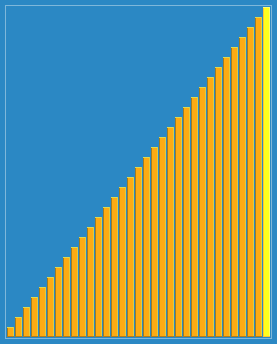
使用希尔排序为一列数字进行排序的过程(图片来源维基百科)
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
//这里我直接用模板函数,如有不懂请看我写的另一篇帖子--两步学会C++模板的使用<1>
template <typename T> //定义Tx参数类型,根据传入的数据类型确定
void Shellsort(vector<T> &numbers)
{//希尔排序
int numlen=numbers.size();
int i,j;
T tmp;
for(int h=numlen/2;h>0;h/=2)
{
for (i=h;i<numlen;i++)
{
for (j=i-h;j>=0;j-=h)
{
if (numbers[j+h]<numbers[j])
{
swap(numbers[j+h],numbers[j]);
}else{
break;
}
}
}
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[]={9,8,7,6,5,4,3,2,1};
char b[]={'j','f','e','d','c','b','a'};
vector<int> numbers(a,a+9);
vector<char> character(b,b+7);
Shellsort(numbers);
Shellsort(character);
for (int i=0;i<numbers.size();i++)
cout<<numbers[i]<<" ";
cout<<endl;
for (int i=0;i<character.size();i++)
cout<<character[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:

5.快速排序
快速排序是对冒泡排序的一种改进。将待排序记录分割成独立的两个部分,其中一部分记录的关键字均小于另一部分记录的关键字,然后再对这两个部分继续进快速排序,直至整个序列有序。

使用快速排序为一列数字进行排序的过程(图片来源维基百科)
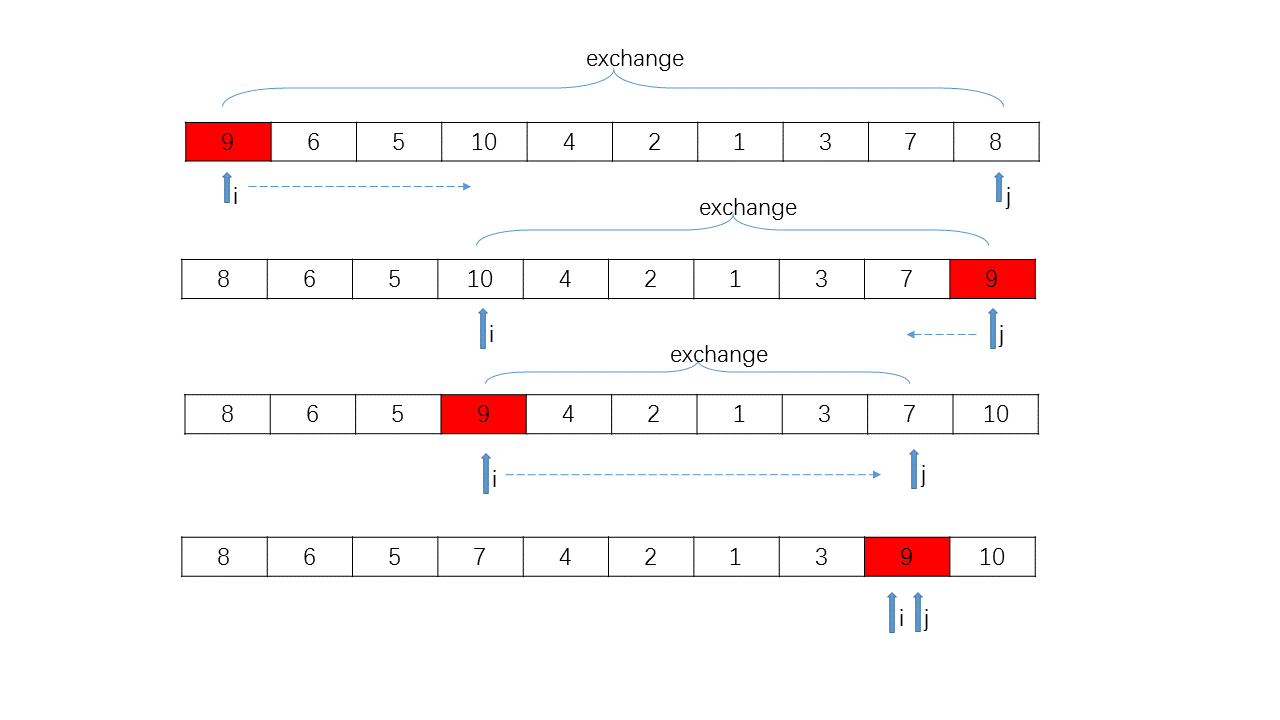
将数组分为9之前的一组和9之后的一组,对这两组继续进行快速排列使用相同的方法
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
//这里我直接用模板函数,如有不懂请看我写的另一篇帖子--两步学会C++模板的使用<1>
template <typename T> //定义Tx参数类型,根据传入的数据类型确定
void Quicksort(vector<T> &numbers, int left, int right){//希尔排序
int i,j;
T tmp;
if(left>=right) return ;
i=left;
j=right;
tmp=numbers[i];
while (i<j)
{
while(i<j&&numbers[j]>=tmp) j--;
if(i<j) swap(numbers[i++],numbers[j]);
while(i<j&&numbers[i]<tmp) i++;
if(i<j) swap(numbers[j--],numbers[i]);
}
Quicksort(numbers,left,i);
Quicksort(numbers,i+1,right);
}
template <typename T>
void sort(vector<T> &a){
Quicksort(a,0,a.size()-1);
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[]={7,1,9,3,2,8,6,4,5};
char b[]={'j','f','e','d','c','b','a'};
vector<int> numbers(a,a+9);
vector<char> character(b,b+7);
sort(numbers);
sort(character);
for (int i=0;i<numbers.size();i++)
cout<<numbers[i]<<" ";
cout<<endl;
for (int i=0;i<character.size();i++)
cout<<character[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:

6.堆排序
堆是一个近似完全二叉树的结构,并同时满足堆的性质,即子结点的键值或索引总是小于(或者大于)它的父节点。在堆的数据结构中,堆中的最大值总是位于根节点(在优先队列中使用堆的话堆中的最小值位于根节点)。堆中定义以下几种操作:
- 最大堆调整(Max_Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 创建最大堆(Build_Max_Heap):将堆所有数据重新排序
- 堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
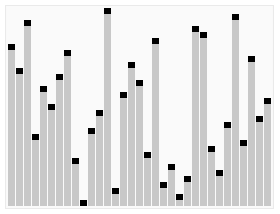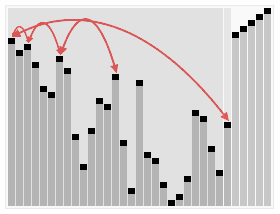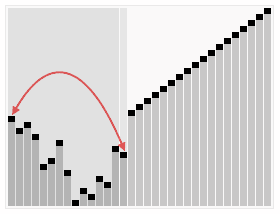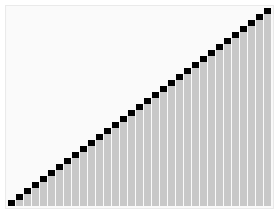
堆排序算法的演示。首先,将元素进行重排,以匹配堆的条件。图中排序过程之前简单的绘出了堆树的结构。(图片来源维基百科)
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
#define Leftchild(i) (i*2+1)
//这里我直接用模板函数,如有不懂请看我写的另一篇帖子--两步学会C++模板的使用<1>
template <typename T> //定义Tx参数类型,根据传入的数据类型确定
void sort(vector<T> &numbers, int i,int len){//希尔排序
int Child;
T tmp;
for (tmp=numbers[i];Leftchild(i)<len;i=Child)
{
Child=Leftchild(i);
if(Child!=len-1&&numbers[Child+1]>numbers[Child]) Child++;
if (tmp<numbers[Child])
numbers[i]=numbers[Child];
else
break;
}
numbers[i]=tmp;
}
template <typename T>
void Heapsort(vector<T> &numbers, int len){
for(int i=len/2;i>=0;i--)
sort(numbers,i,len);
for(int i=len-1;i>0;i--){
swap(numbers[0],numbers[i]);
sort(numbers,0,i);
}
}
template <typename T>
void mergesort(vector<T> &numbers){
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[]={7,1,9,3,2,8,6,4,5};
char b[]={'j','f','e','d','c','b','a'};
vector<int> numbers(a,a+9);
vector<char> character(b,b+7);
Heapsort(numbers,numbers.size());
Heapsort(character,character.size());
for (int i=0;i<numbers.size();i++)
cout<<numbers[i]<<" ";
cout<<endl;
for (int i=0;i<character.size();i++)
cout<<character[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:

7.归并排序
归并排序算法思想:把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

一个归并排序的例子:对一个随机点的链表进行排序(图片来源维基百科)
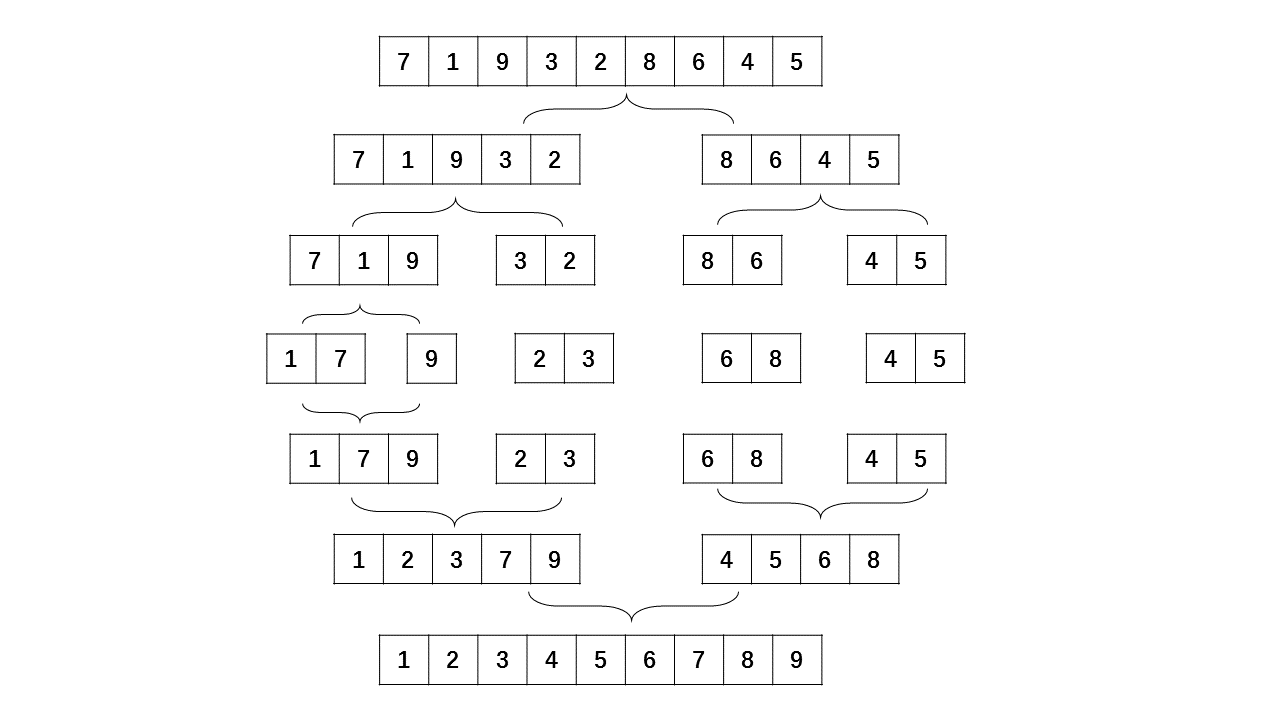
归并排序分解及合并的图解,通过一个缓存容器来临时储存拍好序的小块数据;
图和我预想的易理解程度有偏差,等后续继续完善。
#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
//这里我直接用模板函数,如有不懂请看我写的另一篇帖子--两步学会C++模板的使用<1>
template <typename T> //定义Tx参数类型,根据传入的数据类型确定
void Mergesort(vector<T> &numbers,vector<T> &tmpvec,int left,int right){
if (right>left)
{
int mid = (left+right)/2;
Mergesort(numbers,tmpvec,left,mid);
Mergesort(numbers,tmpvec,mid+1,right);
Msort(numbers,tmpvec,left,mid,right);
}
}
template <typename T>
void Msort(vector<T> &numbers,vector<T> &tmpvec, int left,int mid,int right){
int i,j;
i=left;
j=mid+1;
int len=right-left+1;
int k=0;
while(i<=mid&&j<=right)
{
if (numbers[i]<numbers[j])
tmpvec[k++]=numbers[i++];
else
tmpvec[k++]=numbers[j++];
}
while(i<=mid)
tmpvec[k++]=numbers[i++];
while(j<=right)
tmpvec[k++]=numbers[j++];
for (k=0;k<len;k++)
numbers[left++]=tmpvec[k];
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[]={7,1,9,3,2,8,6,4,5};
char b[]={'j','f','e','d','c','b','a'};
vector<int> numbers(a,a+9);
vector<char> character(b,b+7);
vector<int> numtmp(numbers.size());//为什么要在这里新建一个容器呢?是为了避免在函数内部重复建立容器
vector<char> chartmp(character.size());//所以直接在这里建一个大小刚好的
Mergesort(numbers,numtmp,0,numbers.size()-1);
Mergesort(character,chartmp,0,character.size()-1);
for (int i=0;i<numbers.size();i++)
cout<<numbers[i]<<" ";
cout<<endl;
for (int i=0;i<character.size();i++)
cout<<character[i]<<" ";
cout<<endl;
system("pause");
}
运行结果:

由于笔者能力有限,对于本文有说明不清或错误的点,欢迎在下方评论区探讨。
如需转载请私信告知笔者,并在转载文中附上本文地址






















 1612
1612

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










