先验算法（Apriori Algorithm）原理及python代码实现

先验算法（Apriori Algorithm）是关联规则学习的经典算法之一。先验算法的设计目的是为了处理包含交易信息内容的数据库（例如,顾客购买的商品清单，或者网页常访清单。）而其他的算法则是设计用来寻找无交易信息（如Winepi算法和Minepi算法）或无时间标记（如DNA测序）的数据之间的联系规则。关联分析的目的是从大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式：频繁项集或者关联规则。频繁项集(frequent item sets)是指经常出现在一起的物品的集合，关联关系(association rules)暗示两种物品之间可能存在很强的关系。

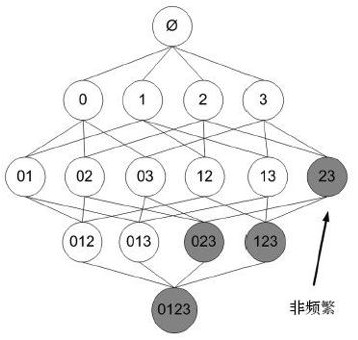
先验算法采用广度优先搜索算法进行搜索并采用树结构来对候选项目集进行高效计数。它通过长度为 k-1的候选项目集来产生长度为k的候选项目集，然后从中删除包含不常见子模式的候选项。根据向下封闭性引理,该候选项目集包含所有长度为  k的频繁项目集。之后，就可以通过扫描交易数据库来决定候选项目集中的频繁项目集。

from __future__ import division, print_function
import numpy as np
import itertools


class Rule():
    def __init__(self, antecedent, concequent, confidence, support):
        self.antecedent = antecedent
        self.concequent = concequent
        self.confidence = confidence
        self.support = support


class Apriori():
    """A method for determining frequent itemsets in a transactional database and
    also for generating rules for those itemsets. 
    Parameters:
    -----------
    min_sup: float
        The minimum fraction of transactions an itemets needs to
        occur in to be deemed frequent
    min_conf: float:
        The minimum fraction of times the antecedent needs to imply
        the concequent to justify rule
    """
    def __init__(self, min_sup=0.3, min_conf=0.81):

        self.min_sup = min_sup
        self.min_conf = min_conf
        self.freq_itemsets = None       # List of freqeuent itemsets
        self.transactions = None        # List of transactions

    def _calculate_support(self, itemset):
        count = 0
        for transaction in self.transactions:
            if self._transaction_contains_items(transaction, itemset):
                count += 1
        support = count / len(self.transactions)
        return support


    def _get_frequent_itemsets(self, candidates):
        """ Prunes the candidates that are not frequent => returns list with 
        only frequent itemsets """
        frequent = []
        # Find frequent items
        for itemset in candidates:
            support = self._calculate_support(itemset)
            if support >= self.min_sup:
                frequent.append(itemset)
        return frequent


    def _has_infrequent_itemsets(self, candidate):
        """ True or false depending on the candidate has any
        subset with size k - 1 that is not in the frequent itemset """
        k = len(candidate)
        # Find all combinations of size k-1 in candidate
        # E.g [1,2,3] => [[1,2],[1,3],[2,3]]
        subsets = list(itertools.combinations(candidate, k - 1))
        for t in subsets:
            # t - is tuple. If size == 1 get the element
            subset = list(t) if len(t) > 1 else t[0]
            if not subset in self.freq_itemsets[-1]:
                return True
        return False


    def _generate_candidates(self, freq_itemset):
        """ Joins the elements in the frequent itemset and prunes
        resulting sets if they contain subsets that have been determined
        to be infrequent. """
        candidates = []
        for itemset1 in freq_itemset:
            for itemset2 in freq_itemset:
                # Valid if every element but the last are the same
                # and the last element in itemset1 is smaller than the last
                # in itemset2
                valid = False
                single_item = isinstance(itemset1, int)
                if single_item and itemset1 < itemset2:
                    valid = True
                elif not single_item and np.array_equal(itemset1[:-1], itemset2[:-1]) and itemset1[-1] < itemset2[-1]:
                    valid = True

                if valid:
                    # JOIN: Add the last element in itemset2 to itemset1 to
                    # create a new candidate
                    if single_item:
                        candidate = [itemset1, itemset2]
                    else:
                        candidate = itemset1 + [itemset2[-1]]
                    # PRUNE: Check if any subset of candidate have been determined
                    # to be infrequent
                    infrequent = self._has_infrequent_itemsets(candidate)
                    if not infrequent:
                        candidates.append(candidate)
        return candidates


    def _transaction_contains_items(self, transaction, items):
        """ True or false depending on each item in the itemset is
        in the transaction """
        # If items is in fact only one item
        if isinstance(items, int):
            return items in transaction
        # Iterate through list of items and make sure that
        # all items are in the transaction
        for item in items:
            if not item in transaction:
                return False
        return True

    def find_frequent_itemsets(self, transactions):
        """ Returns the set of frequent itemsets in the list of transactions """
        self.transactions = transactions
        # Get all unique items in the transactions
        unique_items = set(item for transaction in self.transactions for item in transaction)
        # Get the frequent items
        self.freq_itemsets = [self._get_frequent_itemsets(unique_items)]
        while(True):
            # Generate new candidates from last added frequent itemsets
            candidates = self._generate_candidates(self.freq_itemsets[-1])
            # Get the frequent itemsets among those candidates
            frequent_itemsets = self._get_frequent_itemsets(candidates)

            # If there are no frequent itemsets we're done
            if not frequent_itemsets:
                break

            # Add them to the total list of frequent itemsets and start over
            self.freq_itemsets.append(frequent_itemsets)

        # Flatten the array and return every frequent itemset
        frequent_itemsets = [
            itemset for sublist in self.freq_itemsets for itemset in sublist]
        return frequent_itemsets


    def _rules_from_itemset(self, initial_itemset, itemset):
        """ Recursive function which returns the rules where confidence >= min_confidence
        Starts with large itemset and recursively explores rules for subsets """
        rules = []
        k = len(itemset)
        # Get all combinations of sub-itemsets of size k - 1 from itemset
        # E.g [1,2,3] => [[1,2],[1,3],[2,3]]
        subsets = list(itertools.combinations(itemset, k - 1))
        support = self._calculate_support(initial_itemset)
        for antecedent in subsets:
            # itertools.combinations returns tuples => convert to list
            antecedent = list(antecedent)
            antecedent_support = self._calculate_support(antecedent)
            # Calculate the confidence as sup(A and B) / sup(B), if antecedent
            # is B in an itemset of A and B
            confidence = float("{0:.2f}".format(support / antecedent_support))
            if confidence >= self.min_conf:
                # The concequent is the initial_itemset except for antecedent
                concequent = [itemset for itemset in initial_itemset if not itemset in antecedent]
                # If single item => get item
                if len(antecedent) == 1:
                    antecedent = antecedent[0]
                if len(concequent) == 1:
                    concequent = concequent[0]
                # Create new rule
                rule = Rule(
                        antecedent=antecedent,
                        concequent=concequent,
                        confidence=confidence,
                        support=support)
                rules.append(rule)
                    
                # If there are subsets that could result in rules
                # recursively add rules from subsets
                if k - 1 > 1:
                    rules += self._rules_from_itemset(initial_itemset, antecedent)
        return rules

    def generate_rules(self, transactions):
        self.transactions = transactions
        frequent_itemsets = self.find_frequent_itemsets(transactions)
        # Only consider itemsets of size >= 2 items
        frequent_itemsets = [itemset for itemset in frequent_itemsets if not isinstance(
                itemset, int)]
        rules = []
        for itemset in frequent_itemsets:
            rules += self._rules_from_itemset(itemset, itemset)
        # Remove empty values
        return rules