算法通关村第一关 —— 链表中环的问题(黄金挑战)

目录

算法通关村第一关 —— 链表中环的问题(黄金挑战)

1. 判断是否有环

方法一 使用Hash

方法二 双指针

2. 确定环的入口

方法一 双指针

方法二 三次双指针

---

算法通关村第一关 —— 链表中环的问题(黄金挑战)

1. 判断是否有环

方法一 使用Hash

判断链表中是否有环是链表的经典问题，相对容易一些，最容易的方法是使用Hash，遍历链表的时候将元素放入到map或者set中，如果有环一定会发生碰撞。发送碰撞的位置也就是入口的位置，所以这个题so easy！让我们一起用代码来实现吧！

/**
 * 方法1：通过HashMap判断
 *
 * @param head
 * @return
 */
public static boolean hasCycleByMap(ListNode head) {
    Set<ListNode> set = new HashSet<ListNode>();
    while (head != null) {
        if (!set.add(head)) {
            return true;
        }
        head = head.next;
    }
    return false;
}

方法二 双指针

确定是否有环，最有效的方法其实是双指针。快指针一次走两步，慢指针一次走一步，如果快的能到达表尾就不会有环，如果存在环，那两指针必定会在某个位置相遇。

这里有一个疑问需要解决，因为两者每次走的距离不一样，会不会快的人在快追上的时候跳过去了导致两者不会相遇？

答案是不会！如下图所示，当fast快追上slow时，fast一定距离slow还有一个或者两个空格。

如果只有一个空格，那么如图一所示，下一步fast和slow将在3相遇。

如果有两个空格，那么如图二所示，下一步fast到达3，slow到达4，回到情况1，因此也会相遇。

所以只要有环，两指针必定相遇。下面是具体的实现代码：

/**
* 通过双指针思想
* @param head
* @return
*/
public static boolean hasCycleByTwoPoint(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow)
            return true;
    }
    return false;
}

2. 确定环的入口

方法一 双指针

第一种题型我们已经学会判断是否有环了，那当环存在时，就一定会有入口，那么如何确定入口的位置呢，我们用图的方法来理解比较好。下图中两指针遍历到相遇位置（Z），然后将两只真分别放在表头（X）和相遇位置（Z），并以相同速度前进，则最后将在（Y) 相遇，下面我们来解释原理。

① 快指针多绕了一圈就相遇的情况

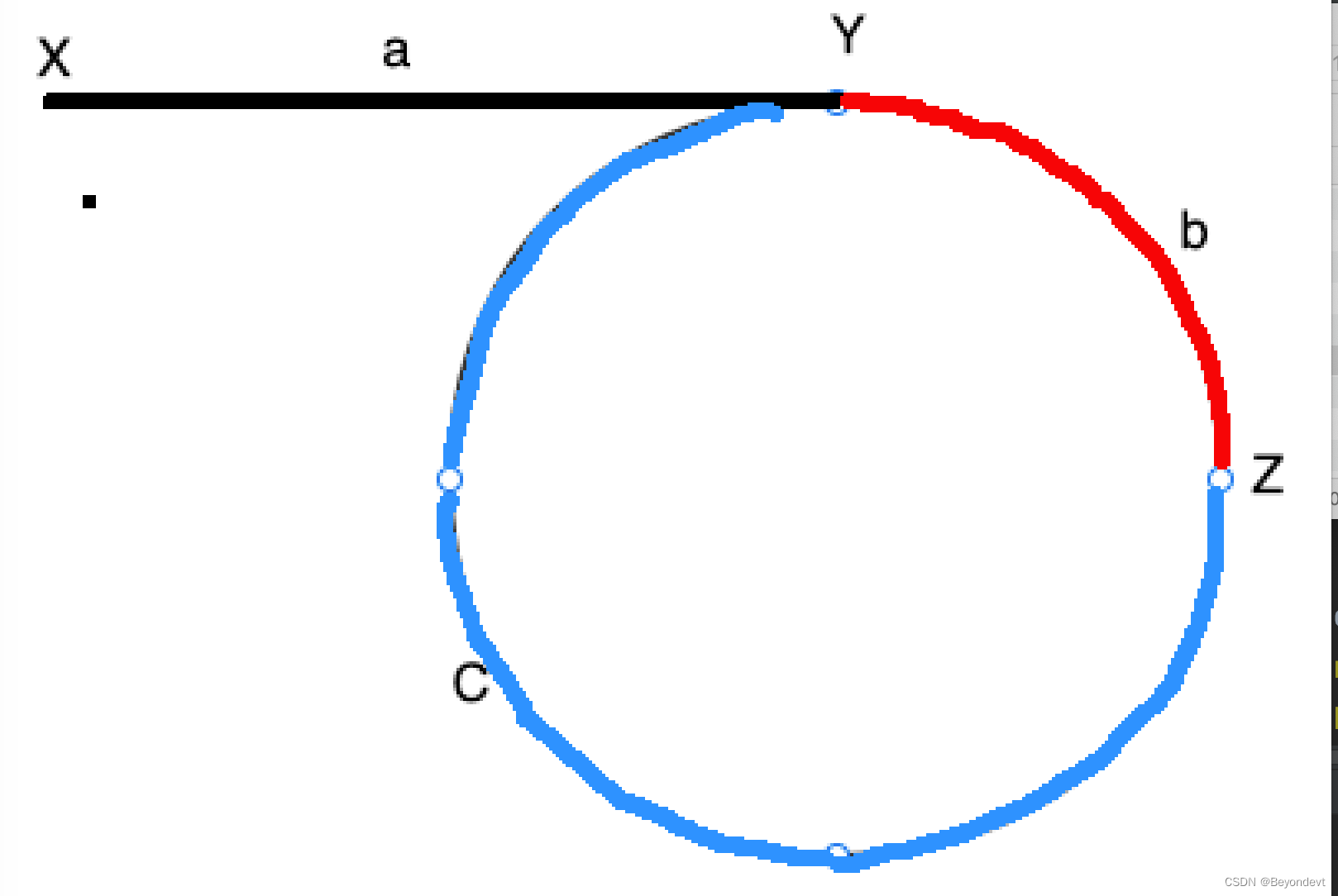
寻找入口过程为：

1）两指针一起遍历到第一次相遇，其中fast一次走两步，slow一次走一步

2）此时fast指针走了a+b+c+b步，slow指针走了a+b步，由行进速度可得以下关系式：

a+b+c+b = 2*(a+b) , 故a = c

因此两指针分别从X和Z以相同速度行进，他们最终一定会在Y点相遇，即为环的起始点。

②  快指针多绕了多圈之后才相遇

如果fast指针在相遇前已经绕了n圈，那么他走过的距离为 a + (n+1)b + nc

此时slow指针只走了a + b, 由行进速度有如下关系式：

a + (n+1)b + nc = 2 *（a+b）,此时b+c为环的长度，设为LEN

则 a = c + (n-1)LEN，说明在第二次相遇的时候，快指针从Z出发已经转了(n-1)圈回到Z，然后两指针再一起向前走c步，此时一起到达Y，则又相遇了，所以也是一样的道理，代码并不会改变，所以第二次相遇的位置就是环的入口。具体实现代码如下所示：

/**
 * 通过双指针实现
 *
 * @param head
 * @return
 */

public static ListNode detectCycleByTwoPoint(ListNode head) {
    if (head == null) {
        return null;
    }
    ListNode slow = head, fast = head;
    // 第一次遍历到相遇
    while (fast != null) {
        slow = slow.next;
        if (fast.next != null) {
            fast = fast.next.next;
        } else {
            return null;
        }
        if (fast == slow) {
            // 第二次遍历到相遇的位置即为环的入口
            ListNode ptr = head;         
            while (ptr != slow) {
                ptr = ptr.next;
                slow = slow.next;
            }
            return ptr;
        }
    }
    return null;
}

方法二 三次双指针

三次双指针的思想其实很好理解，就是如果我们通过两次双指针遍历确定了环的大小K和末尾结点，那么问题就可以退化成找倒数第k个结点了。因为我们知道环的入口就是整个链表刚好遍历一次的倒数第K个结点，K即为环的大小。下面我们用代码来实现以下:

public class Solution {
    // 找到入口
    public ListNode detectCycle(ListNode head) {
        if(head == null){
            return null;
        }
        ListNode slow = head, fast = head;
        // 判断是否相遇
        while(fast != null){
            slow = slow.next;
            if(fast.next !=null){
                fast = fast.next.next;
            }else{
                return null;
            }
            if(fast == slow){
                // 固定一指针，另一个遍历，得到环的长度
                fast = fast.next;
                int len =1;
                while(slow != fast){
                    fast = fast.next;
                    len++;
                }
            // 取到倒数第k个结点，即为环的入口
            return getKthFromEnd(head,len);
            }
        }
    return null;
}

    // 得到倒数第k个结点，注意最后fast ！= null 要改成fast != slow
    public static ListNode getKthFromEnd(ListNode head, int k) {
        ListNode fast = head;
        ListNode slow = head;

        while (fast != null && k > 0) {
            fast = fast.next;
            k--;
        }
        while (fast != slow) {
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}