python实现汉诺塔问题

最新推荐文章于 2024-03-09 16:08:30 发布

原创最新推荐文章于 2024-03-09 16:08:30 发布 · 542 阅读

1 ·

CC 4.0 BY-SA版权

本文详细解析了汉诺塔问题及其递归解决方案，通过实例演示了如何运用递归思想移动不同层数的盘子，从初始状态到达目标状态的过程。文章通过具体的Python代码展示了递归函数的实现，帮助读者理解递归调用的原理。

以下图的三层汉诺塔为例，开始柱指的是开始状态时存放所有盘子的柱子，中转柱指的是中间状态时暂时存放n-1个（三层就是3-1个）盘子的柱子，目标柱指的是盘子最终要移动到的柱子。这里需要注意，开始柱，中转柱，目标柱并不是一成不变的，而是会根据层次的不同而改变。汉诺塔问题可这么简单理解：要解决从下往上数第n个盘子，即从大往小数第n个盘子，首先得解决第n-1个盘子的移动，而第n-1个盘子的移动又得先解决第n-2个盘子的移动。这个过程就是递归过程，从而回到解决第一个盘子如何移动的问题上。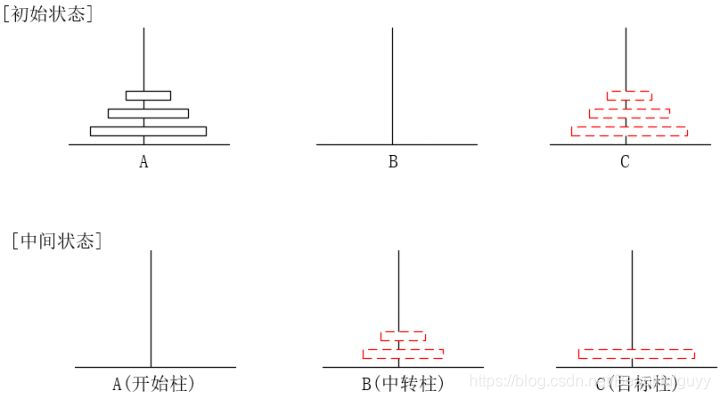在这里插入图片描述
实现的代码和移动途径如下：
def move(n,a,b,c):
if n==1:
print(a,’–>’,c)
else:
move(n-1,a,c,b)
print(a,’–>’,c)
move(n-1,b,a,c)
move(4,‘A’,‘B’,‘C’)