分治算法/分治思想

学习参考来自：lloil的分治算法详解 和 编程帮的分治算法

---

分治算法的基本思想：

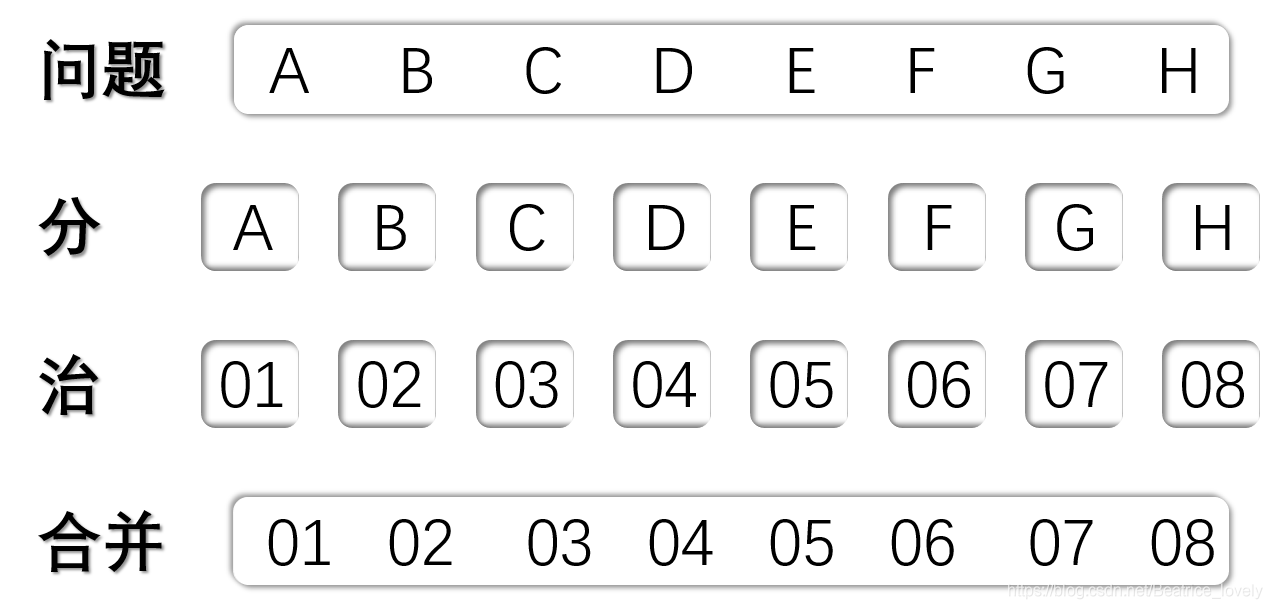
        将一个问题分解为n个相互独立且与原问题性质相同的子问题，通过逐个解决小问题，从而解决整个问题。（逐个击破，分而治之

分治算法是很多高效算法的基础：

        排序算法：快速排序、归并排序、堆排序……

        查找算法：二分查找（折半查找算法）……

        傅立叶变换：快速傅立叶变换……

        各类问题：大整数乘法、棋盘覆盖、汉诺塔……

采用分治算法能解决问题有以下特征： 

• 原问题规模大，不易解决。但原问题可缩小且到一定程度就可以容易解决。

绝大多数问题都可以满足的，问题的计算复杂性一般是随着问题规模的增加而增加。

• 原问题可以分解为多个规模较小、求解方式相似的子问题。且各个子问题之间相互独立、互不影响。

这是应用分治算法的前提，绝大多数问题都可以满足的，反映了递归思想的应用。

• 若干子问题的解进行合并后，可以得到原问题的解。

这是应用分治算法的关键，能否利用分治法完全取决于问题是否满足这点。

如果仅仅具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心算法或动态规划。

• 原问题所分解出的各个子问题是相互独立的。

这与分治算法的效率相关，如果子问题不是相互独立的，那么采用动态规划较好。

分治算法的优缺点：

        分治算法主要用于解决规模较大的问题，通过将大问题“分而治之”将有效降低题目难度。又因为分解得到的子问题之间是相互独立且互不影响的，所以可以同时进行，以此提升解决问题的效率。
        分治算法的缺陷在于，分治算法常常采用递归的方式实现，整个过程需要消耗大量的系统资源，严重时还会导致程序崩溃。

---

        分治重要的是一种思想，注重的是问题分、治、合并的过程。在分治算法中，递归是一种通过方法调用自身形成一个回路的过程，而分治可能就是利用了多次这样的来回过程。

---

分治算法经典问题：

       因为分治算法重要在于理解其思想，还有一些典型的分治算法解决的问题，所以博主在这里主要讲述数组最大值和最小值、汉诺塔问题、二分查找算法、归并算法查找、快速排序算法。

1 数组最大值和最小值

        数组最大值和最小值问题：是指在长度为 n 的数字序列中找到最大的数和最小的数。

1.1 普通算法

        普通算法中：定义两个变量 max 和 min 并将序列中首个数字赋值给他们，从第 2 个数字开始遍历整个序列，如果遍历到的数字比 max 大，将其赋值给 max，如果遍历到数字比 min 小，将其赋值给 min。整个序列遍历完成后，max 记录的是序列中最大的数字，min 记录的是序列中最小的数字。

#include<stdio.h>
int main()
{
	int n;
	scanf("%d",&n);
	int arr[n];  
	for(int i=1;i<=n;i++) // 输入 n 个数字
	{
		scanf("%d",&arr[i]);
	}
	int max,min;
	max = min = arr[1];   // 将第 1 个数字分别赋值给 max 和 min 
	for(int i=2;i<=n;i++)
	{                  // 从第 2 个数字开始遍历
	    if(arr[i]>max)                    // 如果 max 小于遍历到的数字，则更新 max 的值
	        max = arr[i];
	    if(arr[i]<min)                    // 如果 min 小于遍历到的数字，则更新 min 的值
	        min = arr[i];
	}
	printf("max = %d, min = %d", max, min);                  // 输出 max 和 min 的值
	return 0;
 } 

1.2 分治算法

        对于本问题，分治算法就是不断地进行二分，直到分解为不可分的一个数组元素，这个数组元素是最小子问题的最大值也是最小值，之后再逐一合并为原问题的解。

        具体的分治算法可参考：王陸的算法设计与分析——分治法求最大值和最小值

---

2 汉诺塔问题

        请参考博主写的：汉诺塔（Hanoi） ——递归思想

---

3 二分查找算法（折半查找算法）

        二分查找又称折半查找，是一种基于分治思想的快速搜索算法，时间复杂度为O(logn)。
        二分查找算法只适用于有序序列，换句话说，只有保证序列有序的情况下，才能使用二分查找算法。

        二分查找的搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

3750: 二分查找

#include<stdio.h>
int n,m,a[1000001]; //全局变量 
//二分查找（Binary Search） 确认 是否存在 所寻找的值 m 的函数 
int BS(){ 
	int low,mid,high; //二分查找 
	low = 0; high = n-1; //确定位置 
	while(low<=high) //进行寻找操作 
	{
		mid = (low+high)>>1; //>>1 和 /2 操作是一样的 不过网上说>>1的效率高一点 
		if(m>a[mid]) low = mid+1;
		else if(m<a[mid])  high = mid-1;
		else if(m>a[mid-1]) return mid;
		else low = mid - 1;
	}
	return 1;
}
int main()
{
	while(scanf("%d",&n)) //输入值…… 正常操作 
	{
		for(int i=0;i<n;i++)
		scanf("%d",&a[i]);
		scanf("%d",&m);
		if(a[0]==m) printf("1");
		else{
			int flag = BS(); // 插个旗子做记号 是否找到 
			if(flag == 1) //没找到 输出None 
			{
				printf("None\n");
			}
			else
				printf("%d\n",flag+1); //找到了输出flag+1 因为我们是从0开始记数的 
		}
	}
	return 0;
}

        但是博主交上去之后TLE了，不是很懂该怎么改，不想直接用库函数，求大佬指导一下。

---

4 归并算法查找

        归并排序是一种基于分治思想的排序算法，时间复杂度为O(nlogn)，效率仅次于快速排序算法。

5 快速排序算法

        快速排序（简称“快排”）是一种基于分治思想实现的排序算法，它具有排序效率高、消耗资源少、容易实现等优点，是很多实际场景的首选排序算法。