LCS与背包问题

1.问题

LCS：

背包问题：

2.解析

LCS：

背包问题：

3.设计

LCS：
X=<D, C, B, A>
Y=<B, A, C>
m=0-4
n=0-3

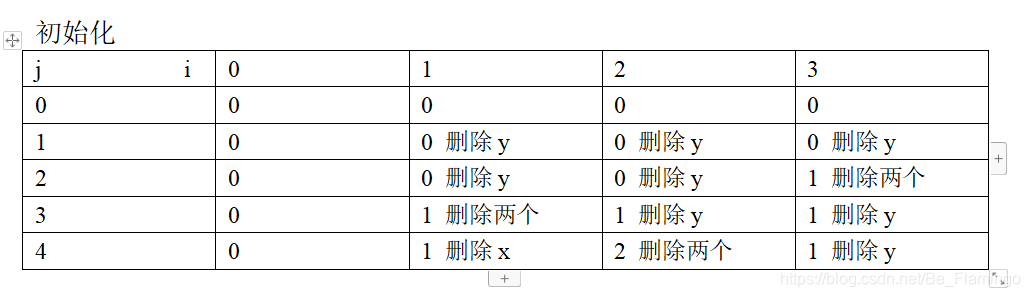
算法一：
(1)i=1
a)j=1 X.D<>Y.B :C[1,1]=max(C[1,0],C[0,1])=max(0,0)=0 删除y
b)j=2 X.D<>Y.A :C[1,2]=max(C[1,1],C[0,2])=max(0,0)=0 删除y
c)j=3 X.D<>Y.C :C[1,3]=max(C[1,2],C[0,3])=max(0,0)=0 删除y

(2)i=2
a)j=1 X.C<>Y.B :C[2,1]=max(C[2,0],C[1,1])=max(0,0)=0 删除y
b)j=2 X.C<>Y.A :C[2,2]=max(C[2,1],C[1,2])=max(0,0)=0 删除y
c)j=3 X.C==Y.C :C[2,3]=C[1,2]+1=1 删除两个

(3)i=3
a) j=1 X.B==Y.B :C[3,1]=C[2,0]+1=1 删除两个
b) j=2 X.B<>Y.A :C[3,2]=max(C[3,1],C[2,2])=max(1,0)=1 删除y
c) j=3 X.B<>Y.C :C[3,3]=max(C[3,2],C[2,3])=max(1,1)=1 删除y

(4)i=4
a) j=1 X.A<>Y.B :C[4,1]=max(C[4,0],C[3,1])=max(0,1)=1 删除x
b) j=2 X.A==Y.A :C[4,2]=C[3,1]+1=2 删除两个
c) j=3 X.A<>Y.C :C[4,3]=max(C[4,2],C[3,3])=max(2,1)=1 删除y

算法二：
1 删除y
X=<D, C, B, A>
Y=<B, A>
2 删除两个
X=<D, C, B>
Y=<,B>
1 删除两个
X=<D, C>
Y=<>
j=0
算法结束，结果为<B,A>

背包问题：
v1=2, v2=4, v3=5, v4=9
w1=3, w2=4, w3=5, w4=6
b=10

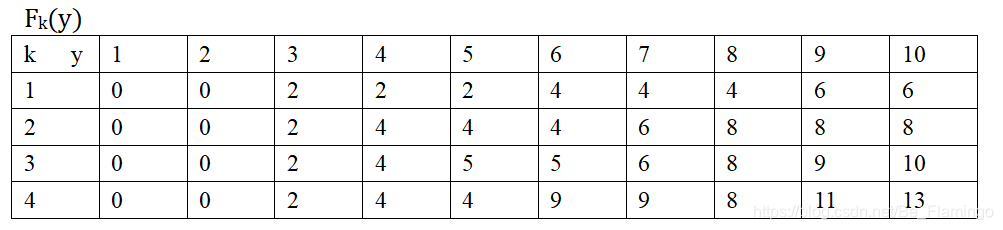
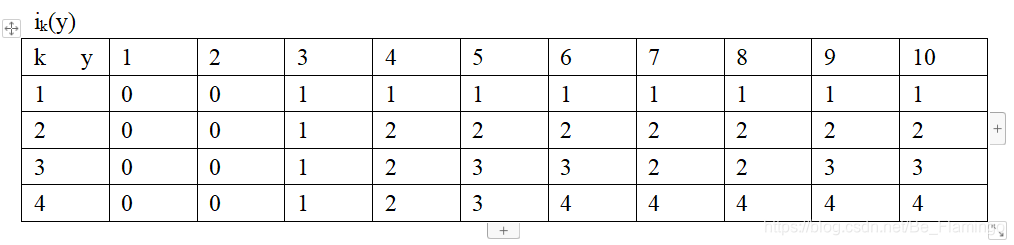
i4(10)=4,则4至少占一个；i4(10-6)=i4(4)=2,则2占一个，4-4=0，最后没有了
所以4号物品占一个，2号物品占一个

4.分析

时间复杂度：LCS：O(mn),背包问题：O(mn)

5.源码

无