莫比乌斯反演

前言

莫比乌斯反演是数论数学中很重要的内容，可以用于解决很多组合数学的问题。莫比乌斯反演的应用非常广泛，内容很多但是结论却并不复杂。
一道经典的莫比乌斯反演题：
求：${\sum }_{i=1}^n{\sum }_{j=1}^m[gcd(i,j)==d]$
也就是说有多少对$(i,j)$的$gcd$为$d$。

---

先知

常见积性函数¹

1.$\sigma (n)$——除数函数。用式子表示为：${\sigma }^k(n)={\sum }_{d|n}{d}^k$。
2.$d(n)$——约数函数。表示n的约数的个数。用式子表示为：$\sigma (n)={\sum }_{d|n}1$，也可写作：$d(n)={\sum }_{d=1}^n[d|n]$ （其实没什么太大区别）。
3.$\sigma (n)$——约数和函数。用式子表示为：$\sigma (n)={\sum }_{d|n}d={\sum }_{d=1}^n[d|n]\cdot d$。
4.$\phi (n)$——欧拉函数。表示不大于n且与n互质的正整数个数，十分常见的数论函数。用式子表示：$\phi (n)={\sum }_{i=1}^n[gcd(n,i)=1]$ 注意：n=1时，$\phi (n)=1$。
5.$\mu (n)$——莫比乌斯函数² 。

常见完全积性函数

1.$ϵ(n)$——元函数。也有人把它叫作e(n),我们只需要知道$ϵ(n)=[n=1]$。($[n=1]$代表if(n==1) n=1; else n=0;)
2.$I(n)$——恒等函数。所谓恒等就是这个函数的值恒为1。
3.$id(n)$——单位函数。$id(n)=n$。
4.$id(n)$——幂函数。$i{d}^k(n)=n^k$。

PS：积性函数有一个特别重要的性质，那就是（积性函数∗积性函数）仍然为积性函数！！！这个性质可以用来判断能否被杜教筛！

接下来就到了狄利克雷卷积，似乎是很高深的东西。

---

狄利克雷卷积³

定义：对于函数$f,g$,定义它们的卷积为$(f\ast g)(n)={\sum }_{d|n}f(d)g(\frac{n}{d})$(d|n代表d是n的因子 )，很明显，所得也是一个数论函数，其中$(f\ast g)$表示为将$f$卷$g$，后面的括号代表范围。(PS：后面的括号一般可以省略不写，默认为n)
很显然，狄利克雷卷积满足以下运算规律,可以类比为乘法的运算法则：
交换律       (f∗g=g∗f)；
结合律       ((f∗g)∗h=f∗(g∗h))；
分配律       ((f+g)∗h=f∗h+g∗h)；

任意函数卷积单位元仍为它本身

不要小看元函数，它充当单位元，当元函数配合上结合律时还可以用来证明一些结论
$d=1\ast 1$
$\sigma =id\ast 1$
因为      $ϵ(n)={\sum }_{d|n}\mu (d)$
所以      $ϵ=1\ast \mu$
因为      $\phi (n)={\sum }_{d|n}\mu (d)\frac{n}{d}$
所以      $\phi =\mu \ast id$
因为      $n={\sum }_{d|n}\phi (d)$
所以      $id=\phi \ast 1$

莫比乌斯函数$\mu$

莫比乌斯反演定理形式一：
$$F(n)=\sum _{d|n}f(d)=>f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})$$
证明：
变形得到：
$$f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})=\sum _{d|n}\mu (d)\sum _{k|\frac{n}{d}}f(k)=\sum _{k|n}f(k)\sum _{d|\frac{n}{k}}\mu (d)$$
因为
$$\sum _{d|n}\mu (d)=\{\begin{array}{l}1,n=1\\ 0,n>1\end{array}$$
所以当且仅当$\frac{n}{k}=1$，即$n=k$，${\sum }_{d|\frac{n}{k}}\mu (d)=1$，其余时间为0。
故
$$\sum _{k|n}f(k)\sum _{d|\frac{n}{k}}\mu (d)=f(n)$$
莫比乌斯反演定理形式二：
$$F(n)=\sum _{n|d}f(d)=>f(n)=\sum _{n|d}\mu (\frac{d}{n})F(d)$$
证明：
令$k=\frac{d}{n}$，得到
$$f(n)=\sum _{k=1}^{+\infty }\mu (k)F(nk)=\sum _{k=1}^{+\infty }\mu (k)\sum _{nk|t}f(t)=\sum _{n|t}f(t)\sum _{k|\frac{t}{n}}\mu (k)$$
所以当且仅当$\frac{t}{n}=1$，即$t=n$，${\sum }_{k|\frac{t}{n}}\mu (k)=1$，其余时间为0。
故
$$\sum _{n|t}f(t)\sum _{k|\frac{t}{n}}\mu (k)=f(n)$$
证毕。

欧拉函数 $\phi$

欧拉函数为积性函数(若$m、n$互质，有$\phi (m)\phi (n)=\phi (mn)$)
欧拉函数φ(n)定义为，1~n中与n的最大公约数为1的数字的个数。例如 φ(5) = 4, φ(6) = 2
　　若$p$为质数，显然 $\phi (p)=p-1$
　　若$n=p^k$， 则n的大于1的约数有$p,2p,3p,...(p^{k-1}-2)p,(p^{k-1}-1)p$共$p^{k-1}$个数。所以$\phi (n)=p^k-p^{k-1}$
欧拉函数有一个很著名的性质：${\sum }_{d|n}\phi (d)=n$。
因为

所以对于任意

或者写成这种形式：
　
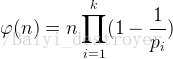
莫比乌斯函数和欧拉函数的关系：

---

杜教筛

考虑如何求μ的前缀和
比如说$10^{10}$？ 线筛会T。这时我们就需要杜教筛了。
杜教筛是以低于线性的时间复杂度来计算积性函数的前缀和的神奇筛法！
即我们需要计算的式子为：${\sum }_{i=1}^{n}f(i)$($f(i)$为积性函数)

杜教筛的套路式

我们构造两个积性函数$h$和$g$。使得$h=f\ast g$。记$S(n)={\sum }_{i=1}^{n}f(i)$。
$$\sum _{i=1}^{n}h(i)=\sum _{i=1}^n\sum _{d|i}g(d)f(\frac{i}{d})$$
$$\to \sum _{d=1}^{n}g(d)\sum _{i=1}^{[\frac{n}{d}]}f(i)$$
$$\to \sum _{i=1}^{n}h(i)=\sum _{d=1}^{n}g(d)\ast S(\lfloor \frac{n}{d}\rfloor )$$
接着，我们将右边式子的第一项给提出来，可以得到：
$$\sum _{i=1}^{n}h(i)=g(1)\ast S(n)+\sum _{d=2}^{n}g(d)\ast S(\lfloor \frac{n}{d}\rfloor )$$
$$\to g(1)\ast S(n)=\sum _{i=1}^{n}h(i)-\sum _{d=2}^{n}g(d)\ast S(\lfloor \frac{n}{d}\rfloor )$$
其中的$h(i)=(f\ast g)(i)$；
经各种分析，只要当你的$h(i)$的前缀和很好求，能在较短的时间内求出，那么当我们对后面的式子进行整除分块时，求$S(n)$的复杂度为$O(n^{\frac{2}{3}})$。对于$g$与$h$需要从我们对狄利克雷卷积中的各种式子的熟悉和仔细观察式子的能力中得到。

应用

一：求$S(n)={\sum }_{i=1}^n\mu (i)$；
根据那个套路式：$g(1)S(n)={\sum }_{i=1}^n(f\ast g)(i)-{\sum }_{d=2}^{n}g(d)\cdot S(\lfloor \frac{n}{d}\rfloor )$，我们只需要找一个积性函数$g$使得这个函数与μ的卷积的前缀和容易求。如果你认真的看了上文，应该就可以很轻松的想到一个积性函数$I$。
我们知道$\mu \ast I=ϵ$，很显然，单位元的前缀和非常好求，就是1，并且$I$十分方便整除分块。所以我们把这个积性函数带入上述式子中可以得到：
$$S(n)=1-\sum _{d=2}^{n}S(\lfloor \frac{n}{d}\rfloor )$$
这就是杜教筛莫比乌斯函数的前缀和。
二：求$S(n)={\sum }_{i=1}^n\phi (i)$
与求莫比乌斯函数的思路类似。
我们在脑海中找到一个与欧拉函数有关的卷积式子：$\phi \ast I=id$
我们可以发现，在筛欧拉函数前缀和所选择的积性函数g同样也是I哟！代入得：
$$S(n)=\sum _{i=1}^{n}i-\sum _{d=2}^{n}S(\lfloor \frac{n}{d}\rfloor )$$
前面那个式子可以利用等差数列求和公式$O(1)$的计算出结果，后面同样利用整除分块。
所以，我们又学会了如何筛欧拉函数的前缀和啦！
三：求$S(n)={\sum }_{i=1}^{n}i\cdot \phi (i)$
这个式子是不是无法一眼看出需要配什么积性函数了呢？
我们考虑狄利克雷卷积的形式：${\sum }_{d|n}(d\cdot \phi (d))\cdot g(\frac{n}{d})$
我们看前面这个$d$不太爽，考虑后面配出一个积性函数使得这个$d$能够被约掉。因此，我们尝试将$g$配成$id$。这样就可以把$d$给弄没！代入得：
$$\sum _{d|n}(d\cdot \phi (d))\cdot \frac{n}{d}=\sum _{d|n}n\cdot \phi (d)$$$$\to =n\sum _{d|n}\phi (d)=n^2$$
我们惊喜的发现，似乎配对了！！！
得：
$$S(n)=\sum _{i=1}^n{i}^2-\sum _{d=2}^{n}d\cdot S(\lfloor \frac{n}{d}\rfloor )$$
对于这个式子，我们前面可以利用平方和的公式$O(1)$算出结果，后面的式子利用等差数列求和公式进行整除分块。

我们可以通过以上的思路求得这个看似无法筛的积性函数的前缀和。

代码实现
我们首先先线筛出数据范围根号左右的积性函数的前缀和。再递归的实现杜教筛。特别要注意的是，杜教筛筛出的前缀和一定要存下来！！！
如果你比较的勤劳，那就去手写hash，如果你想偷懒，那就最好用stl中的unordered_map，最好不要用map，平白无故多个log的复杂度，何必呢…
还有一点，一定要记得取模！！！以及，判断要不要开long long，搞不好你TLE就是因为取模去多了，或者long long开多啦！

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int maxx = 10000001 * 2;
bool isprime[maxx];
int prime[maxx/10];
int mu[maxx];
int countp;
map<long long,int> mp;
void Get_mu(int maxn)  //求莫比乌斯函数
{
    memset(isprime,1,sizeof(isprime));
    isprime[1] = true;
    mu[1] = 1;
    for(int i=2; i<=maxn; i++)
    {
        if(isprime[i])
            prime[++countp] = i, mu[i] = -1;
        for(int j=1; i*prime[j]<=maxn&&j<=countp; j++)
        {
            int t = i * prime[j];
            isprime[t] = false;
            if(!(i%prime[j]))
            {
                mu[t] = 0;
                break;
            }
            else mu[t] = -mu[i];
        }
    }
}
long long n,m;
long long nn,top;
long long ans;
int get(long long x)
{
    int sum = 0;
    for(long long i=2; i<=x; i++)
    {
        long long zz = x/i;
        long long next = x/zz;
        if(zz <= top)
            sum += (next-i+1) * mu[zz];
        else
        {
            if(mp[zz])
                sum += (next-i+1) * (mp[zz]);
            else
                sum += (next-i+1) * get(zz);
        }
        i = next;
    }
    if(x>top)
        mp[x] = (1-sum);
    return (1-sum);
}

int main()
{
    cin>>n>>m;
    top = maxx-1;
    Get_mu(maxx-1);
    for(int i=1; i<=top; i++)
        mu[i]+=mu[i-1];
    ans = get((long long)m) - get((long long)(n-1));
    cout<<ans<<endl;
}

---

莫比乌斯函数

莫比乌斯函数是一个由容斥系数所构成的函数。

$\mu (d)$的定义是:

• 当$d=1$时，$\mu (d)=1$；
• 当$d={\Pi }_{i=1}^k{p}_i$且$p_i$为互异素数时，$\mu (d)=(-1{)}^k$。(说直白点，就是$d$分解质因数后，没有幂次大于平方的质因子，此时函数值根据分解的个数决定)；
  只要当$d$含有任何质因子的幂次大于2，则函数值为0.
  即
  $$\mu (x)=\{\begin{array}{l}1，x=1\\ 0，x存在平方因子\\ -1，x有奇数个质因子（包括x是质数）\\ 1，x有偶数个质因子\end{array}$$
  当然，莫比乌斯函数也有很多有趣的性质：
• 对于任意正整数$n$，${\sum }_{d|n}\mu (d)=[n=1]。$（$[n=1]$表示只有当$n=1$成立时，返回值为1；否则，值为0；(这个就是用$\mu$是容斥系数的性质可以证明)(PS:这一条性质是莫比乌斯反演中最常用的)
• 对于任意正整数n，∑d|nμ(d)d=ϕ(n)n。（这个性质很奇妙，它把欧拉函数和莫比乌斯函数结合起来，或许我之后写杜教筛的学习笔记时会去证明吧）

程序实现并不难，求$\mu (x)$。

1. 打表：

//线性筛法求莫比乌斯函数
bool check[MAX+10];
int prime[MAX+10];
int mu[MAX+10];
void Moblus()
{
    memset(check,false,sizeof(check));
    mu[1] = 1;
    int tot = 0;
    for(int i = 2; i <= MAX; i++)
    {
        if( !check[i] )
        {
            prime[tot++] = i;
            mu[i] = -1;
        }
        for(int j = 0; j < tot; j++)
        {
            if(i * prime[j] > MAX)
                break;
            check[i * prime[j]] = true;
            if( i % prime[j] == 0)
            {
                mu[i * prime[j]] = 0;
                break;
            }
            else
            {
                mu[i * prime[j]] = -mu[i];
            }
        }
    }
}

2. 非打表：

ll getmob(ll a)
{
    ll x=a,tmp=a;
    int cnt=0,now=0;
    for(ll j=2; j*j<=x; j++)
    {
        now=0;
        if(x%j==0)
        {
            while(x%j==0)
                now++,x/=j;
            if(now>1)
                return 0;
            cnt++;
        }
    }
    if(x!=1)
        cnt++;
    return (cnt&1)?-1:1;
}

莫比乌斯反演

莫比乌斯反演是数论中的重要内容，在许多情况下能够简化运算。

我们考虑以下列函数：
$$F(n)=\sum _{d|n}f(d)$$
可推导得：
$$f(n)=\sum _{d|n}\mu (d)F(\lfloor \frac{n}{d}\rfloor )$$
这就称作莫比乌斯反演定理。

莫比乌斯反演证明

莫比乌斯反演的证明有两种方式。
定义证明方法：
$$\sum _{d|n}\mu (d)F(\lfloor \frac{n}{d}\rfloor )$$
$$=\sum _{d|n}\mu (d)\sum _{i|\lfloor \frac{n}{d}\rfloor }f(i)（1）$$
$$=\sum _{i|n}f(i)\sum _{d|\lfloor \frac{n}{i}\rfloor }\mu (d)（2）$$
当$\frac{n}{i}=1$,即$n=i$时，（2）式才不为0。所以（2）式只剩下$f(n)$一项了。
$$=f(n)$$
莫比乌斯反演还有另外的一种形式，当F(n)和f(n)满足：
$$F(n)=\sum _{n|d}f(d)$$
可以推出：
$$f(n)=\sum _{n|d}\mu (\frac{d}{n})F(d)$$

莫比乌斯反演公式总结

约数的莫比乌斯反演：
若：$f(n)={\sum }_{d|n}g(d)$
则：$g(n)={\sum }_{d|n}\mu (d)f(\frac{n}{d})$
倍数的莫比乌斯反演：
若：$f(n)={\sum }_{n|d}g(d)$
则：$g(n)={\sum }_{n|d}\mu (\frac{d}{n})f(d)$

---

借鉴自：https://www.cnblogs.com/peng-ym/p/8647856.html

---

1. [积性函数百度百科]
   (https://baike.baidu.com/item/积性函数/8354949?fr=aladdin) ↩︎

2. 莫比乌斯百度百科 ↩︎

3. [狄利克雷卷积百度百科]
   (https://baike.baidu.com/item/狄利克雷乘积/18903903?fr=aladdin) ↩︎