<think>嗯，用户想知道如何判断三维空间中的一个点是否在给定的四面体内部。首先，我得回忆一下四面体的结构。四面体是三维空间中最简单的多面体，由四个三角形面组成。要判断点是否在内部，可能需要利用几何方法或者坐标系的转换。
记得以前学过，可以通过体积比较的方法。四面体由四个顶点组成，假设这四个顶点是A、B、C、D。如果点P在四面体内部，那么由P和四个面组成的小四面体的体积之和应该等于原四面体的体积。如果总和相等，那么P在内部；否则，在外部。不过这个方法需要计算五个四面体的体积，可能计算量较大，但数学上可行。
另一个方法可能是使用重心坐标（Barycentric Coordinates）。在二维中，判断点是否在三角形内可以通过重心坐标是否都在0到1之间来实现。三维中，四面体的重心坐标可能有四个参数，需要满足非负且相加为1的条件。不过具体怎么计算，可能需要进一步推导。
或者，利用向量和平面方程。对于四面体的每个面，可以确定点P是否在面的同一侧。如果点P相对于所有四个面都在内部，那么就在四面体内。具体来说，每个面对应一个平面方程，计算点P代入平面方程后的符号是否与顶点在另一侧的符号一致。如果四个面都满足，则点在内。
需要确认每个面的平面方程如何构建。假设有一个面由三个点A、B、C组成，那么该平面的法向量可以通过向量AB和AC的叉乘得到。然后平面方程可以表示为：(n·(X - A)) = 0，其中n是法向量，X是平面上的任意点。对于点P，代入方程后的结果符号可以判断其在平面的哪一侧。比如，四面体内部的点应该在所有四个面的同一侧，即对于每个面来说，点P应该满足与第四个顶点D的位置相同的一侧。
举个例子，对于面ABC，计算点P与点D相对于该面的位置是否相同。如果点D在面ABC的正方向一侧，那么点P也应该在该方向，否则在内部。同样的方法应用到其他三个面，如果都满足，则点P在内部。
这时候可能需要具体公式。假设平面方程的法向量n由AB×AC得到，那么点D代入平面方程的值应该是正的或负的，取决于法向量的方向。然后点P代入的结果符号需要与D的相同。对于四个面都进行这样的检查，若全部满足，则点在内。
另外，是否要考虑数值计算的误差？比如，当点恰好位于某个面上时，如何处理。这时候可能需要一个容差范围，但用户的问题可能暂时不需要考虑这种情况，只需判断内部或外部。
另外，有没有更高效的方法？比如，使用矩阵行列式或者参数方程来解这个问题。比如，将点P表示为四面体四个顶点的线性组合，系数满足非负且和为1的条件。这其实就是重心坐标的思路。具体来说，点P可以表示为P = aA + bB + cC + dD，其中a + b + c + d = 1，并且a, b, c, d ≥ 0。如果存在这样的系数，则点P在四面体内部。
如何求解这些系数呢？可能需要解线性方程组。比如，将坐标表示为四个顶点坐标的组合，通过解方程组来找到系数。不过这可能涉及到四个方程（x、y、z坐标和系数之和为1）解四个未知数，但三维空间中的点可能无法直接解，需要引入齐次坐标或者调整方程。
或者，使用体积坐标的方法。每个系数对应于对应顶点所对面与点P形成的小四面体的体积与原四面体体积的比例。例如，a等于四面体PBCD的体积与原四面体ABCD的体积的比值，同样，b、c、d对应其他三个小四面体的体积比例。如果这四个系数都是非负的，并且总和为1，则点P在内部。
这样的话，计算每个小四面体的体积，并检查它们的总和是否等于原体积，同时每个体积比例非负。这可能和体积比较的方法是一致的。
总结起来，可能的步骤是：
1. 计算原四面体ABCD的体积V。
2. 计算四个小四面体PBCD、PACD、PABD、PABC的体积V1、V2、V3、V4。
3. 如果V1 + V2 + V3 + V4 = V，并且每个Vi都是正数或零，则点P在四面体内部。
不过这里需要注意的是，当点P位于某个面上时，对应的Vi可能为零，但总和仍等于V。这时候需要明确是否将面上的点视为内部。根据用户的问题，可能只需要判断严格内部，或者包括边界。这可能需要根据具体应用调整。
另一个问题是如何计算四面体的体积。三维空间中，四面体的体积可以通过标量三重积计算：V = |(AB · (AC × AD))| / 6，其中AB、AC、AD是从顶点A出发的三个向量。同样，每个小四面体的体积可以用同样的方式计算。
例如，V1（PBCD）的体积是 |(PB · (PC × PD))| / 6。这样计算每个小四面体的体积，然后比较总和是否等于原体积，并且每个体积非负。如果满足，则点P在内部。
但这个方法计算量较大，需要计算四次三重积，可能效率不高，但对于计算机来说还是可行的，特别是当需要高精度的时候。
或者，使用平面方程的符号方法，每个面检查点P是否在内部。这种方法可能更高效，因为只需要计算四个面的平面方程，然后代入点P的坐标，检查符号是否与内部区域一致。
具体来说，对于每个面，比如面BCD，需要确定该面的方程，并确定顶点A在面的哪一侧。然后检查点P是否与A在同一侧。如果是，则对于该面来说，点P在内部。同样处理其他三个面。如果四个面都满足，则点P在四面体内。
如何构造每个面的平面方程？假设面BCD的三个点是B、C、D。计算该面的法向量n = (C - B) × (D - B)。平面方程可以写成n·(X - B) = 0。顶点A是否在该面的正方向侧，可以通过代入A到平面方程中的结果来判断。假设结果为s，如果s > 0，则A在正方向侧。点P代入平面方程的结果s_p的符号需要与s相同，才能说明点P和A在同一侧，即在四面体内。
如果四个面都满足这个条件，那么点P就在四面体内部。
这个方法需要为每个面计算法向量，并代入点坐标，计算四个面的方程，然后进行符号比较。相对于体积法，可能计算量更少，因为不需要计算体积，只需要点积运算。
现在的问题是，如何确保每个面的法向量方向正确，即顶点A在该面的正确侧。可能需要统一法向量的方向，或者根据结果调整符号。
例如，对于面BCD，计算法向量n = (C - B) × (D - B)，然后将顶点A代入平面方程的值：n·(A - B)。如果这个值为正，说明A在法向量指向的一侧。此时，点P要满足n·(P - B) >= 0才能在该面的同一侧。同样处理其他三个面。
但是四面体的每个面都需要处理，每个面的平面方程需要正确构造，确保内部方向的一致性。
这样，四个面的检查都是必要的，每个面都需要点P和对应顶点（即该面对面的顶点）在同一侧。
如果这四个条件都满足，那么点P在四面体内部。
综上，可能的步骤是：
对于四面体的四个面中的每一个面：
1. 确定该面的三个顶点，例如面BCD的三个顶点是B、C、D。
2. 计算该面的法向量n = (C - B) × (D - B)。
3. 计算该面的平面方程，例如n·(X - B) = 0。
4. 计算顶点A（该面的对面顶点）代入该方程的值s_A = n·(A - B)。
5. 计算点P代入该方程的值s_P = n·(P - B)。
6. 检查s_P和s_A的符号是否相同（即同号或其中一个为零）。如果符号不同，则点P在该面的外部，整个四面体内部判断失败。
如果所有四个面都通过检查，则点P在四面体内部。
这种方法需要注意法向量的方向是否正确，即是否指向四面体内部。如果s_A的值为正，则法向量指向A所在的一侧，即四面体内部。因此，点P需要满足s_P >= 0（如果允许在面上）或者s_P > 0（如果只考虑严格内部）。
这种方法的关键是正确计算每个面的法向量，并确保符号的判断正确。此外，需要注意数值计算的精度问题，比如当s_P非常接近零时，可能由于浮点误差导致误判。
因此，在实现时，可能需要使用一定的容差范围，比如当s_P的值在-ε到+ε之间时，视为在面上，可以根据需求决定是否视为内部。
总结起来，两种主要方法是体积法和平面方程符号法。体积法直观但计算量大，符号法更高效但需要注意法向量的方向。
此外，还有参数法，利用重心坐标的参数来判断。点P是否在四面体内，可以通过解线性方程组得到四个参数，并检查是否都非负且和为1。
具体来说，设四面体顶点为A、B、C、D，点P的坐标可以表示为：
P = A + u*(B - A) + v*(C - A) + w*(D - A)
其中u, v, w ≥ 0，且u + v + w ≤ 1。或者转化为四个参数，使得：
P = αA + βB + γC + δD，其中α + β + γ + δ = 1，且α, β, γ, δ ≥ 0.
解这个方程组，如果存在这样的参数，则点P在四面体内。
如何解这个方程组？可以将点P的坐标表示为四个顶点坐标的线性组合，系数和为1。这相当于解一个线性方程组，可能用矩阵求逆或克莱姆法则。
例如，设A的坐标为(xa, ya, za)，B、C、D同理，点P的坐标为(xp, yp, zp)。则方程组可以写成：
α*xa + β*xb + γ*xc + δ*xd = xp
α*ya + β*yb + γ*yc + δ*yd = yp
α*za + β*zb + γ*zc + δ*zd = zp
α + β + γ + δ = 1
这是一个四元一次方程组，但只有三个空间坐标方程和一个系数和方程。可以用矩阵形式表示为：
| xa xb xc xd | | α | | xp |
| ya yb yc yd | * | β | = | yp |
| za zb zc zd | | γ | | zp |
| 1 1 1 1 | | δ | | 1 |
这可能需要用广义逆矩阵来解，或者转化为三个变量，例如设δ = 1 - α - β - γ，代入前三个方程求解。
不过这可能比较复杂，特别是当矩阵不可逆时。此外，计算参数后需要检查是否都非负。
因此，这种方法在实现时可能比较复杂，尤其是需要考虑数值稳定性。
综上，最常用的方法可能是平面方程符号法，因为它计算量相对较小，且容易实现。每个面只需要计算法向量，代入点坐标进行符号判断即可。
现在，我需要将这种方法整理成步骤，用中文清晰地解释，并给出公式和可能的代码示例。同时，根据用户提供的引用，可能需要参考相关资源。例如，引用[3]提到GJK算法中使用单纯形，而四面体是3阶单纯形。虽然这可能与问题直接关联不大，但可能涉及相关几何算法。
最后，根据用户的要求，生成相关问题，并确保使用正确的LaTeX格式，行内公式用$...$，独立公式用$$...$$，并引用相关文献。</think>要判断三维空间中的点$P$是否位于四面体$ABCD$内部，可以使用**平面方程符号检验法**或**重心坐标法**。以下是具体步骤：
---
### **方法一：平面方程符号检验法**
1. **计算每个面的法向量**
对于四面体的四个面（如面$BCD$），选取三个顶点（$B$、$C$、$D$），计算法向量：
$$ \mathbf{n} = (\mathbf{C} - \mathbf{B}) \times (\mathbf{D} - \mathbf{B}) $$
2. **构造平面方程**
面$BCD$的平面方程为：
$$ \mathbf{n} \cdot (\mathbf{X} - \mathbf{B}) = 0 $$
3. **确定内部方向**
计算顶点$A$（面的对面顶点）代入平面方程的值$s_A = \mathbf{n} \cdot (\mathbf{A} - \mathbf{B})$，若$s_A > 0$，则四面体内部位于该面的正方向侧。
4. **检验点$P$的位置**
计算$s_P = \mathbf{n} \cdot (\mathbf{P} - \mathbf{B})$，若$s_P$与$s_A$同号（即$s_P \geq 0$），则$P$在该面的内部侧。
**需对所有四个面重复此步骤**。若所有面均满足，则$P$在四面体内。
---
### **方法二：重心坐标法**
将点$P$表示为四面体顶点的线性组合：
$$ \mathbf{P} = \alpha \mathbf{A} + \beta \mathbf{B} + \gamma \mathbf{C} + \delta \mathbf{D} $$
需满足以下条件：
$$ \alpha + \beta + \gamma + \delta = 1 \quad \text{且} \quad \alpha, \beta, \gamma, \delta \geq 0 $$
若存在这样的参数，则$P$在四面体内。
---
### **代码示例（Python）**
```python
import numpy as np
def is_point_inside_tetrahedron(P, A, B, C, D):
def check_side(v1, v2, v3, opposite_vertex, point):
n = np.cross(v2 - v1, v3 - v1)
s_opposite = np.dot(n, opposite_vertex - v1)
s_point = np.dot(n, point - v1)
return (s_opposite * s_point) >= 0 # 允许在面上时用>=，否则用>
return (check_side(B, C, D, A, P) and
check_side(A, C, D, B, P) and
check_side(A, B, D, C, P) and
check_side(A, B, C, D, P))
# 示例用法
A = np.array([0, 0, 0])
B = np.array([1, 0, 0])
C = np.array([0, 1, 0])
D = np.array([0, 0, 1])
P = np.array([0.2, 0.2, 0.2])
print(is_point_inside_tetrahedron(P, A, B, C, D)) # 输出: True
```
---
### **关键公式**
1. **法向量计算**：
$$ \mathbf{n} = (\mathbf{C} - \mathbf{B}) \times (\mathbf{D} - \mathbf{B}) $$
2. **平面方程符号检验**：
$$ \text{若} \quad \mathbf{n} \cdot (\mathbf{P} - \mathbf{B}) \cdot \mathbf{n} \cdot (\mathbf{A} - \mathbf{B}) \geq 0 \quad \text{则同侧} $$
---
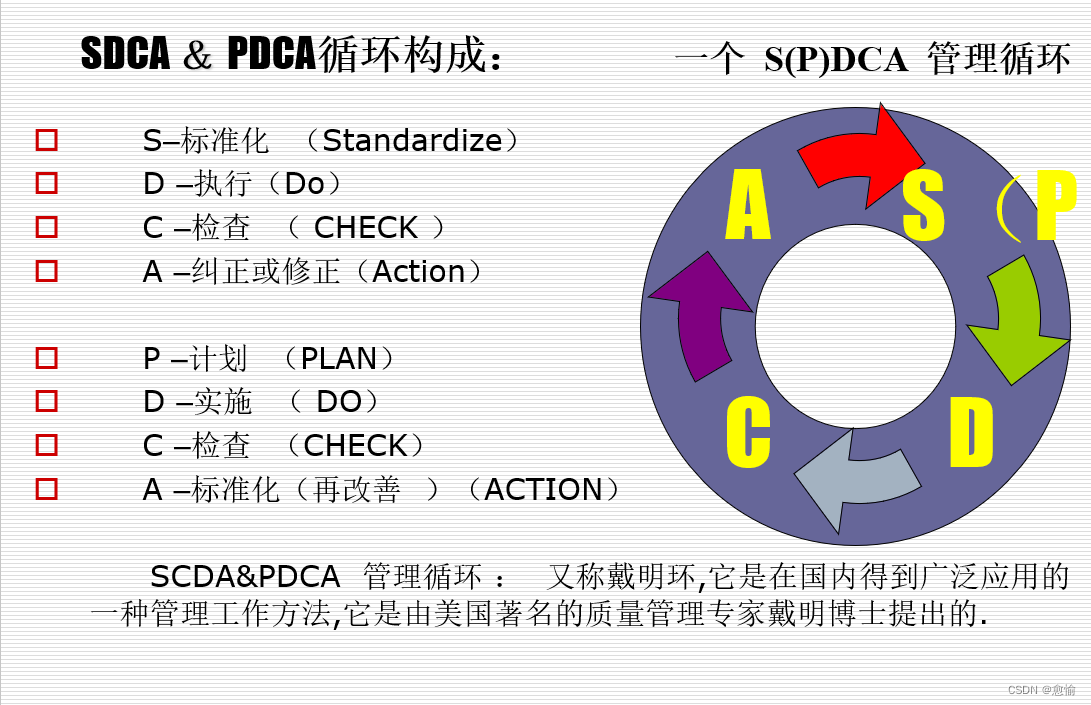
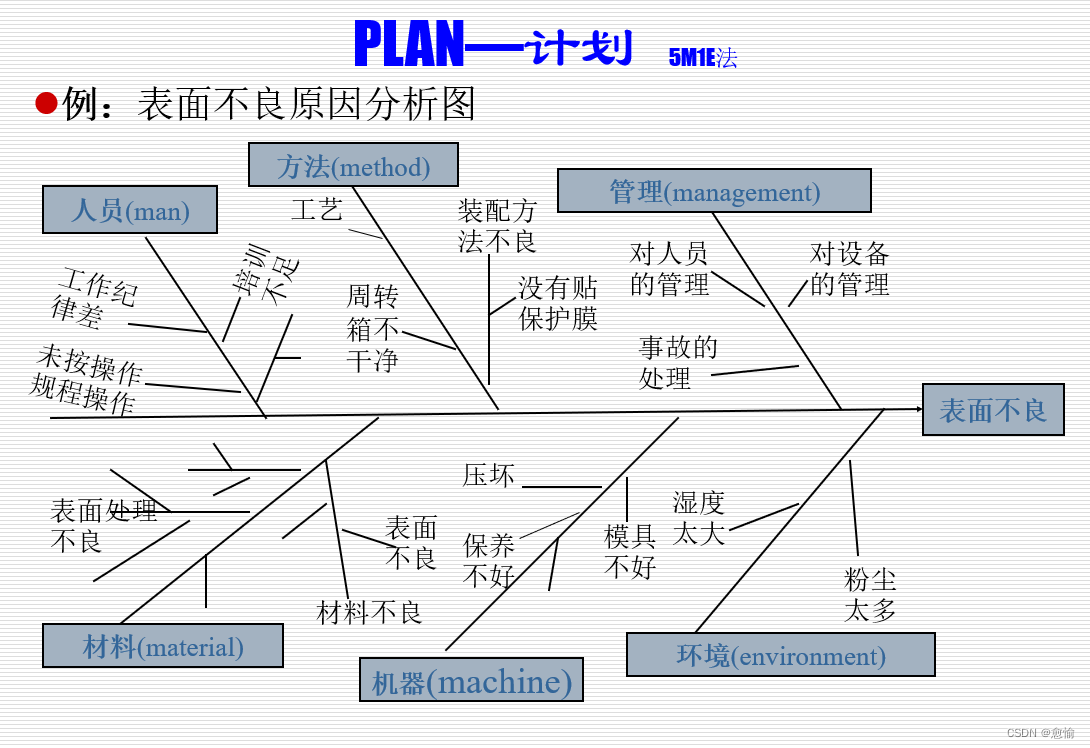
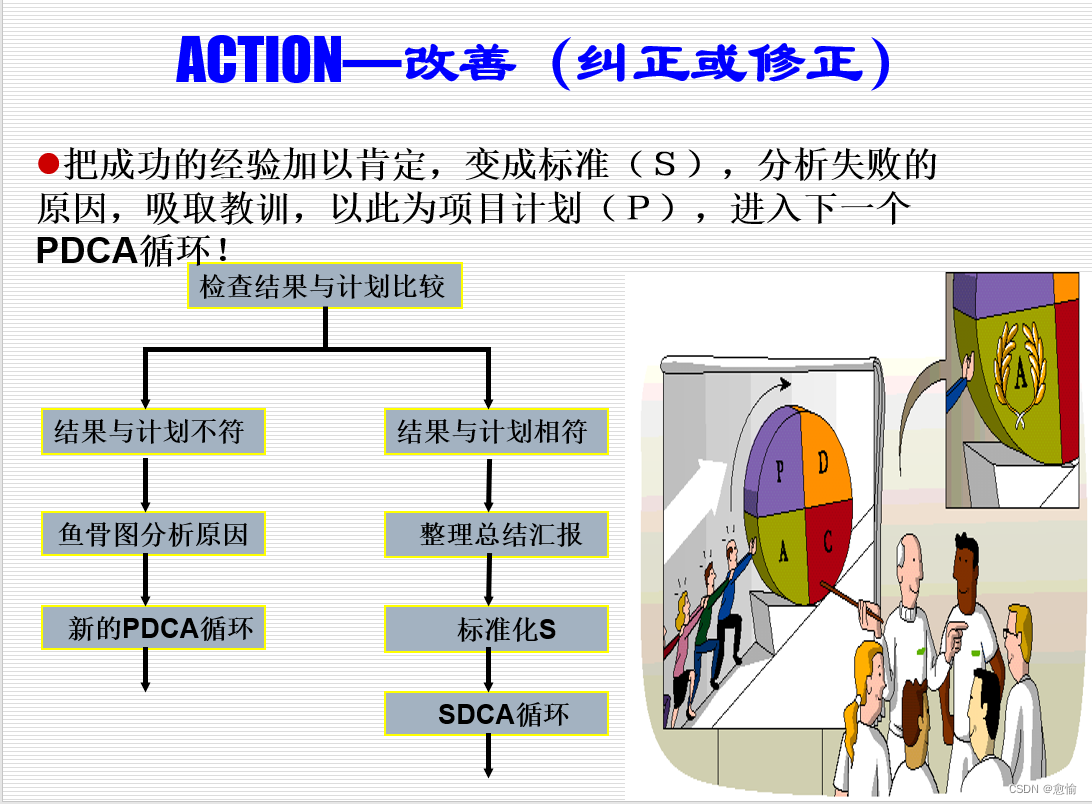
本文探讨了管理的定义，强调了PDCA循环在管理中的重要性，包括计划(Plan)、执行(Do)、检查(Check)和行动(Act)四个阶段。通过实例解析，阐述管理者如何运用PDCA解决问题并持续改进。
扫一扫
868
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
