北太天元在金融建模中的应用：GARCH模型为例

以下内容为卢朓老师在B站进行的分享，可以作为学习参考：

GARCH族模型，即广义自回归条件异方差模型（Generalized Autoregressive Conditional Heteroskedasticity Model），是一类用于估计时间序列数据波动率的统计模型。该模型由Bollerslev在1986年提出，是对ARCH（自回归条件异方差）模型的一种重要扩展。GARCH模型在金融时间序列分析中具有广泛的应用价值，尤其是在金融市场波动性的建模和预测方面。

一、GARCH模型的基本概念

GARCH模型主要用于描述时间序列数据（如股票价格、汇率、利率等）的波动性特征。传统计量经济学假设时间序列变量的波动幅度（方差）是固定的，但这往往不符合实际情况。例如，股票收益的波动幅度通常会随时间变化，表现出聚集性特征，即大的波动后面往往跟着大的波动，小的波动后面往往跟着小的波动。GARCH模型通过引入条件异方差来描述这种波动性聚集现象，从而更准确地捕捉时间序列数据的波动性特征。

二、GARCH模型的结构

GARCH模型通常由两部分组成：均值方程和方差方程。

均值方程：通常是一个ARMA（自回归移动平均）模型，用于描述时间序列数据的线性关系。它表示时间序列数据在某一时刻的期望值，即数据的均值部分。

方差方程：是GARCH模型的核心，用于描述时间序列数据的波动性。方差方程是一个自回归移动平均模型，但作用于时间序列的方差上，而不是直接作用于时间序列数据本身。通过考虑过去的波动率和误差项，方差方程能够预测未来的波动率。

三、GARCH模型的数学表达式

GARCH模型的均值方程通常用于描述时间序列数据的条件均值，即数据在给定信息集下的期望值。然而，值得注意的是，GARCH模型的核心在于其方差方程，该方程用于刻画时间序列数据的条件异方差性，即波动性。尽管如此，在构建GARCH模型时，通常也会同时指定一个均值方程。

对于GARCH模型的均值方程，其形式可以相对简单，也可以相对复杂，具体取决于数据的特性和研究目的。一个常见的均值方程认为时间序列数据的均值是恒定的。这种方程形式适用于数据围绕某个固定水平波动的情况。

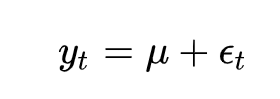
添加图片注释，不超过 140 字（可选）

其中，y_t 是t时刻的观测值， \mu 是常数均值，\epsilon_t 是残差项。

在GARCH模型中，残差项 $\epsilon_t$ 通常被表示为条件方差 $\sigma_t$ 和一个独立同分布（iid）的随机变量 $z_t$ 的乘积，即