第10章《基本数据结构》：栈、队列、双向链表，python实现

栈和队列

栈和队列都是动态集合，栈（stack）实现的是一种后进先出策略，而队列实现的是一种先进先出策略

• 栈：栈上的insert操作称为压入（push），而无元素的delete操作称为弹出（pop），如下图所示，可以用一个数组$S[1..n]$来实现一个最多容纳$n$个元素的栈，该数组有一个属性$S.top$，指向最新插入元素，栈中包含的元素为$S[1..S.top]$，其中$S[1]$是栈底元素，而$S[S.top]$是栈顶元素
  
  当$S.top=0$时，不包含任何元素，即栈是空的，对一个空栈进行弹出操作时，则称栈下溢，这通常是一个错误，如果$S.top$超过了$n$，则称栈上溢
  python实现栈的基本操作如下：

#栈的基本操作
class Stack(object):
	#栈初始化为空
	def __init__(self):
		self.stack = []
	def isempty(self):
		return len(self.stack)==0
	#入栈
	def push(self, item):
		self.stack.append(item)
	#出栈
	def pop(self):
		return self.stack.pop()
	def size(self):
		return len(self.stack)

• 队列：队列上的insert操作称为入队，delete操作称为出队，队列有队头（head）和队尾（tail），当$Q.head=Q.tail$时，队列为空，当$Q.head=Q.tail+1$时，队列是满的。如下图所示，$Q[1..12]$实现队列的一种方式，
  
  其中(a)队列包含5个元素，位于$Q[7..11]$，(b)中依次入队17，3，5元素，（c）中出队元素15
  python实现队列基本操作如下：

#队列的基本操作
class Queue(object):
	def __init__(self):
		self.queue = []
	def isempty(self):
		return len(self.queue)==0
	#入队列
	def enqueue(self,item):
		self.queue.insert(0,item)
	#出队列
	def dequeue(self):
		self.queue.pop()
	def size(self):
		return len(self.queue)

链表

链表是一种这样的数据结构，其中各对象按照线性顺序排列，数组的线性顺序是由数组下标决定的，然而与数组不同的是，链表的顺序是由各个对象里的指针决定的。

• 双向链表：每个元素都是一个对象，每个元素有一个关键字key和两个指针：$next$和$prev$，设$x$为链表的一个元素，$x.next$指向它在链表的后继元素，$x.prev$则指向它的前驱元素，$x.pre=NIL$，则元素$x$没有前驱，即链表的头（head），如果$x.next=NIL$，则元素$x$没有后继，是链表的最后一个元素，即链表的尾（tail）
  
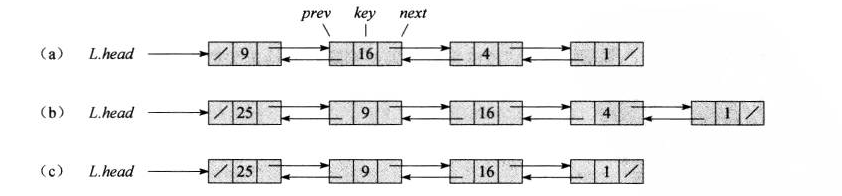
  链表可以有多种形式，它可以是单链接的或者多链接的，可以是已排序的或者未排序的，可以是循环的或非循环的。
  python实现双向链表的基本操作：

# -*-coding:utf8 -*-
import sys

#定义节点
class Node(object):
	def __init__(self, key):
		self.key = key
		self.prev = None
		self.next = None
#定义双向链表
class DoubleList(object):
	def __init__(self):
		#链表头
		self.head = Node(None)
		#链表长
		self.length = 0
	
	#判断链表是否为空
	def isEmpty(self):
		if self.length==0:
			return True
		return False

	#遍历链表
	def traversal(self):
		if self.length == 0:
			return []
		#定义游标
		cur = self.head
		keys = list()
		for i in range(self.length):
			keys.append(cur.next.key)
			cur = cur.next
		return keys

	#插入链表头
	def insert_head(self, key):
		#构造新节点
		new_node = Node(key)
		#插入到表头 O(1)
		new_node.next = self.head.next
		new_node.prev = self.head
		self.head.next = new_node
		#链表长度加1
		self.length+=1

	#插入位置i
	def insert_pos(self, pos, key):
		#判断pos的有效性
		if isinstance(pos,int):
			if pos < 0 or pos>self.length :
				insert_head(key)
			else:
				new_code = Node(key)
				cur = self.head
				for i in range(self.length):
					if i==pos:
						# 设置新节点prev和next指向
						new_node.prev = cur
						new_node.next = cur.next
						# 更新指向新节点的节点
						cur.next = new_code
						new_code.next.prev = new_code
						# 链表长度更新
						self.length+=1
					else:
						cur = cur.next
		else:
			print("pos位置无效")

	#删除元素
	def delete(self, key):
		if self.isEmpty():
			print("list is empty")
		else:
			cur = self.head
			for i in range(self.length):
				if cur.next.key == key:
					if cur.next.next is None:
						#尾部节点删除
						cur.next = None
					else:
						#中间节点
						cur.next = cur.next.next
						cur.next.prev = cur
					#更新链表长度
					self.length-=1
				else:
					cur = cur.next
	#链表的搜索
	def search(self, key):
		cur = self.head
		for i in range(self.length):
			if cur.key != key:
				cur = cur.next
		return cur

if __name__ =="__main__":
	example = DoubleList()
	#插入元素
	for i in range(8):
		example.insert_head(i)
	#遍历
	print(example.traversal())
	#链表的长度
	print(example.length)
	#删除
	example.delete(3)
	print(example.traversal())
	print(example.length)
	#搜索
	x = example.search(4)
	print(x.key)

有根树的表示

• 二叉树：树的节点用对象表示，与链表类似，在二叉树中，如下图所示，属性$p$，$left$，$right$，存放指向父节点，左孩子和右孩子的指针，如果$x.p=NIL$，则$x$是根节点，如果节点$x$没有左孩子，则$x.left=NIL$，右孩子情况类似，属性$T.root$指向整颗树$T$的根节点，如果$T.root=NIL$，则该树为空。
  

• 分支无限制的有根树：二叉树的表示方法可以推广到每个节点的孩子树至多为常数$k$的任意类型树，只需要$left$和$right$属性用$chil{d}_1，chil{d}_2，...，chil{d}_k$代替，但当孩子节点无限制时，这种方法就失效了，所幸的是，有一个巧妙的方法可以用来表示孩子数任意的树，该方法对任意$n$个节点的有根树，只需要$O(n)$的存储空间，这种左孩子右兄弟表示方法（$left-child，right-sibling$）如下图所示，每个节点都包含父节点$T$，每个节点不是包含指向每个孩子的指针，而是只有两个指针：1. $x$.left-child指向节点$x$最左边的孩子节点；2.$x$.right-sibling指向$x$右侧相邻的兄弟节点。如果节点$x$没有孩子节点，则$x$.left-child=$NIL$，如果节点$x$是其父节点的最右孩子，则$x$.right-sibling=$NIL$
  
  数$T$的左孩子右兄弟表示法，每个节点都$x$都有属性$x.p$（上），$x$.left-child（左下），$x$.right-sibling（右下），关键字$key$在图中未显示。