【面试高频题】难度 3/5，数学与并查集的结合

最新推荐文章于 2025-12-13 11:21:53 发布

原创最新推荐文章于 2025-12-13 11:21:53 发布 · 90 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#面试 #算法 #c++

这篇文章讨论了LeetCode上的一道难题，即根据共同的质因数在给定数组中构建图并找到最大连通组件的大小。解决方案涉及质因数分解数组元素，然后使用并查集来维护连通性，从而避免了O(n^2)的复杂度，优化为O(nM)，其中n是数组长度，M是数组中最大值。提供的Java和TypeScript代码实现了这一算法，同时维持了较低的空间复杂度。

题目描述

这是 LeetCode 上的 952. 按公因数计算最大组件大小 ，难度为困难。

Tag : 「数学」、「并查集」

给定一个由不同正整数的组成的非空数组 nums，考虑下面的图：

有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
只有当 nums[i] 和 nums[j] 共用一个大于 11 的公因数时，nums[i] 和 nums[j]之间才有一条边。

返回图中最大连通组件的大小。

示例 1：

输入：nums = [4,6,15,35]

输出：4
复制代码

示例 2：

输入：nums = [20,50,9,63]

输出：2
复制代码

示例 3：

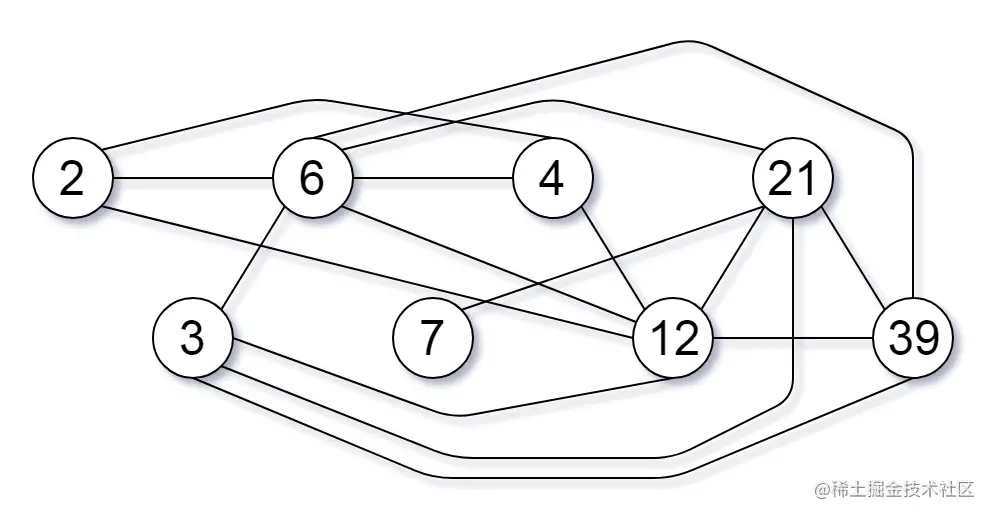
输入：nums = [2,3,6,7,4,12,21,39]

输出：8
复制代码

提示：

1<=��.��ℎ<=2×1041<=nums.length<=2×104
1<=��[�]<=1051<=nums[i]<=105
nums 中所有值都不同

枚举质因数 + 并查集

先考虑如何使用 nums 进行建图，nums 大小为 �=2×104n=2×104，枚举所有点对并通过判断两数之间是否存在边的做法复杂度为 �(�2�)O(n2M)（其中 �=1�5M=1e5 为 ��[�]nums[i] 的最大值），无须考虑。

而不通过「枚举点 + 求公约数」的建图方式，可以对 ��[�]nums[i] 进行质因数分解（复杂度为 �(��[�])O(nums[i])），假设其分解出来的质因数集合为 �S，我们可以建立从 ��Sk 到 ��[�]nums[i] 的映射关系，若 ��[�]nums[i] 与 ��[�]nums[j] 存在边，则 ��[�]nums[i] 和 ��[�]nums[j] 至少会被同一个质因数所映射。

维护连通块数量可以使用「并查集」来做，维护映射关系可以使用「哈希表」来做。

维护映射关系时，使用质因数为 key，下标值 �i 为 value（我们使用下标 �i 作为点编号，而不是使用 ��[�]nums[i] ，是利用��[�]nums[i] 各不相同，从而将并查集数组大小从 1�51e5 收窄到 2×1042×104)。

同时在使用「并查集」维护连通块时，同步维护每个连通块大小 sz 以及当前最大的连通块大小 ans。

Java 代码：

class Solution {
    static int N = 20010;
    static int[] p = new int[N], sz = new int[N];
    int ans = 1;
    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
    void union(int a, int b) {
        if (find(a) == find(b)) return ;
        sz[find(a)] += sz[find(b)];
        p[find(b)] = p[find(a)];
        ans = Math.max(ans, sz[find(a)]);
    }
    public int largestComponentSize(int[] nums) {
        int n = nums.length;
        Map<Integer, List<Integer>> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            int cur = nums[i];
            for (int j = 2; j * j <= cur; j++) {
                if (cur % j == 0) add(map, j, i);
                while (cur % j == 0) cur /= j;
            }
            if (cur > 1) add(map, cur, i);
        }
        for (int i = 0; i <= n; i++) {
            p[i] = i; sz[i] = 1;
        }
        for (int key : map.keySet()) {
            List<Integer> list = map.get(key);
            for (int i = 1; i < list.size(); i++) union(list.get(0), list.get(i));
        }
        return ans;
    }
    void add(Map<Integer, List<Integer>> map, int key, int val) {
        List<Integer> list = map.getOrDefault(key, new ArrayList<>());
        list.add(val);
        map.put(key, list);
    }
}
复制代码

TypeScript 代码：

const N = 20010
const p: number[] = new Array<number>(N), sz = new Array<number>(N)
let ans = 0
function find(x: number): number {
    if (p[x] != x) p[x] = find(p[x])
    return p[x]
}
function union(a: number, b: number): void {
    if (find(a) == find(b)) return 
    sz[find(a)] += sz[find(b)]
    p[find(b)] = p[find(a)]
    ans = Math.max(ans, sz[find(a)])
}
function largestComponentSize(nums: number[]): number {
    const n = nums.length
    const map: Map<number, Array<number>> = new Map<number, Array<number>>()
    for (let i = 0; i < n; i++) {
        let cur = nums[i]
        for (let j = 2; j * j <= cur; j++) {
            if (cur % j == 0) add(map, j, i)
            while (cur % j == 0) cur /= j
        }
        if (cur > 1) add(map, cur, i)
    }
    for (let i = 0; i < n; i++) {
        p[i] = i; sz[i] = 1
    }
    ans = 1
    for (const key of map.keys()) {
        const list = map.get(key)
        for (let i = 1; i < list.length; i++) union(list[0], list[i])
    }
    return ans
};
function add(map: Map<number, Array<number>>, key: number, val: number): void {
    let list = map.get(key)
    if (list == null) list = new Array<number>()
    list.push(val)
    map.set(key, list)
}
复制代码