夯实算法-路径总和 III

原创于 2022-12-12 09:45:36 发布 · 108 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #leetcode

本文解析了LeetCode上一道关于二叉树路径总和的问题，通过深度优先搜索（DFS）结合哈希表的方法，高效地求解二叉树中节点值之和等于特定值的路径数量。

题目：LeetCode

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

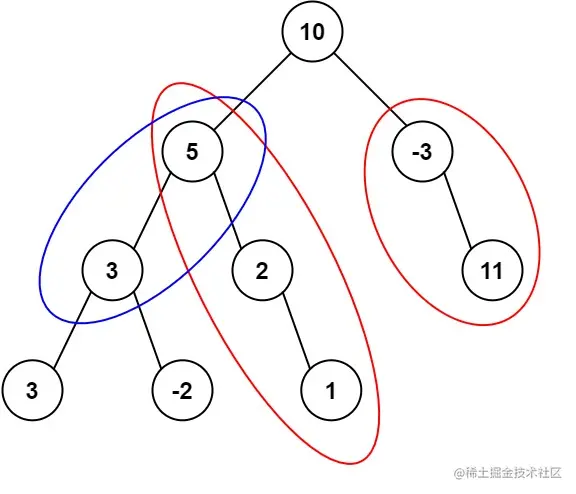
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
复制代码

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3
复制代码

提示:

二叉树的节点个数的范围是 [0,1000]
−109<=Node.val<=109-10^9 <= Node.val <= 10^9−109<=Node.val<=109
−1000<=targetSum<=1000-1000 <= targetSum <= 1000−1000<=targetSum<=1000

解题思路

根据题意是求子路径的和为某个值的数量，路径是从根节点到叶子节点，子路径也就是在极节点与叶子节点中间的一段。这其实是数组中子数组问题的变种，可以借助哈希表的思想来解决，把从0，到n-1的Si先放入一个哈希表中，键为Si，值是其出现的个数。然后再尝试寻找Si-k的个数，记Si=sum[0, i]，其中i=[0, n-1]，那么子数组S[j-1, k]的和可用Sk - Sj来计算。也就是用前缀和。 DFS遍历一遍就可以找到结果。

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public int pathSum(TreeNode root, int targetSum) {
    Map<Integer, Integer> sumMap = new HashMap<>();
    sumMap.put(0, 1);

    return dfs(root, targetSum, sumMap, 0);
}

private static int dfs(TreeNode root, int targetSum, Map<Integer, Integer> sumMap, int path) {
    if (root == null) {
        return 0;
    }
    path += root.val;
    int count = sumMap.getOrDefault(path - targetSum, 0);
    sumMap.put(path, sumMap.getOrDefault(path, 0) + 1);
    count += dfs(root.left, targetSum, sumMap, path);
    count += dfs(root.right, targetSum, sumMap, path);
    sumMap.put(path, sumMap.get(path) - 1);
    return count;
}
复制代码