C++进阶—哈希

第一章：unordered系列关联式容器

在C++98中，STL提供了底层为红黑树结构的一系列关联式容器，在查询时效率可达到log₂N，即最差情况下需要比较红黑树的高度次，当树中的节点非常多时，查询效率也不理想。最好的查询是，进行很少的比较次数就能够将元素找到，因此在C++11中，STL又提供了4个unordered系列的关联式容器，这四个容器与红黑树结构的关联式容器使用方式基本类似，只是其底层结构不同，本文中只对unordered_map和unordered_set进行介绍，unordered_multimap和unordered_multiset可查看文档介绍。

1.1 unordered_map

unordered_map在线文档说明

1. unordered_map是存储<key, value>键值对的关联式容器，其允许通过keys快速的索引到与其对应的value。
2. 在unordered_map中，键值通常用于唯一的标识元素，而映射值是一个对象，其内容与此键关联。键和映射值的类型可能不同。
3. 在内部,unordered_map没有对<key, value>按照任何特定的顺序排序, 为了能在常数范围内找到key所对应的value，unordered_map将相同哈希值的键值对放在相同的桶中。
4. unordered_map容器通过key访问单个元素要比map快，但它通常在遍历元素子集的范围迭代方面效率较低。
5. unordered_map实现了直接访问操作符(operator[])，它允许使用key作为参数直接访问value。
6. 它的迭代器至少是前向迭代器。

1.1.2 unordered_map的接口说明

1. unordered_map的构造

函数声明	功能介绍
unordered_map	构造不同格式的unordered_map对象

2. unordered_map的容量

函数声明	功能介绍
bool empty() const	检测unordered_map是否为空
size_t size() const	获取unordered_map的有效元素个数

3. unordered_map的迭代器

函数声明	功能介绍
begin	返回unordered_map第一个元素的迭代器
end	返回unordered_map最后一个元素下一个位置的迭代器
cbegin	返回unordered_map第一个元素的const迭代器
cend	返回unordered_map最后一个元素下一个位置的const迭代器

4. unordered_map的元素访问

函数声明	功能介绍
operator[]	返回与key对应的value，没有一个默认值

注意：该函数中实际调用哈希桶的插入操作，用参数key与V()构造一个默认值往底层哈希桶中插入，如果key不在哈希桶中，插入成功，返回V()，插入失败，说明key已经在哈希桶中，将key对应的value返回。

5. unordered_map的查询

函数声明	功能介绍
iterator find(const K& key)	返回key在哈希桶中的位置
size_t count(const K& key)	返回哈希桶中关键码为key的键值对的个数

注意：unordered_map中key是不能重复的，因此count函数的返回值最大为1

6. unordered_map的修改操作

函数声明	功能介绍
insert	向容器中插入键值对
erase	删除容器中的键值对
void clear()	清空容器中有效元素个数
void swap(unordered_map&)	交换两个容器中的元素

7. unordered_map的桶操作

函数声明	功能介绍
size_t bucket_count()const	返回哈希桶中桶的总个数
size_t bucket_size(size_t n)const	返回n号桶中有效元素的总个数
size_t bucket(const K& key)	返回元素key所在的桶号

1.2 unordered_set

参见 unordered_set在线文档说明

1.3 在线OJ

1. 961. 在长度 2N 的数组中找出重复 N 次的元素 - 力扣（LeetCode）

class Solution {
public:
    int repeatedNTimes(vector<int>& nums) {
        size_t n = nums.size() / 2;
        //用unordered_map统计每个元素出现的次数
        unordered_map<int, int> m;
        for (auto e : nums)
            m[e]++;
        
        // 找出出现次数为N的元素
        for (auto& e : m)
            if (e.second == n)
                return e.first;
        return 0;
    }
};

2. 349. 两个数组的交集 - 力扣（LeetCode）

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        //一个vector的数据插入到set中，用另一个vector的元素来查找不可以行
        //因为两个vector中都可能会有重复数据
        //nums1 = [1,2,2,1], nums2 = [2,2]
        //如果用nums2里的两个2去set中查找都会有，无法判断

        //set可以排序+去重
        set<int> map1(nums1.begin(), nums1.end());
        set<int> map2(nums2.begin(), nums2.end());

        //找交集 - 双指针
        //set1：4 5 8    set2：4 8 9
        //1.相同就是交集值，同时++
        //2.不相同，小的++。因为排过序，小的不会和另一个map后面的值相同
        //有一个结束就结束

        set<int>:: iterator it1 = map1.begin();
        auto it2 = map2.begin();
        vector<int> v;
        while (it1 != map1.end() && it2 != map2.end()) {
            if (*it1 < *it2) 
                ++it1;
            else if (*it2 < *it1)
                ++it2;               
            else{
                v.push_back(*it1);
                ++it1;
                ++it2;
            }
        }
        return v;
    }
    //找差集
    //1.相同，同时++
    //2.不相同，小的++。小的是差集，因为排过序，小的不会和另一个map后面的值相同
    //一个结束，另一个是差集
};

use of unordered_map.cpp

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <string>
#include <set>
#include <unordered_set>
#include <unordered_map>
using namespace std;

int main() {
	unordered_set<int> s;
	s.insert(5);
	s.insert(2);
	s.insert(6);
	s.insert(1);
	s.insert(4);
	unordered_set<int>::iterator it = s.begin();
	while (it != s.end()) {
		cout << *it << " ";
		++it;
	}
	cout << endl;

	for (auto e : s)
		cout << e << " ";
	cout << endl;

	unordered_map<string, string> dict;
	dict["sort"];//插入
	dict["sort"] = "排序";//修改
	dict["string"] = "字符串";//插入+修改
	dict["abc"] = "xxx";//插入+修改
	for (auto& kv : dict)
		cout << kv.first << ":" << kv.second << endl;

	return 0;
}



//验证性能
int main() {
	const size_t N = 1000000;

	unordered_set<int> us;
	set<int> s;

	vector<int> v;
	v.reserve(N);
	srand((size_t)time(0));
	for (size_t i = 0; i < N; ++i) {
		//v.push_back(rand()); // N比较大时，重复值比较多
		//v.push_back(rand()+i); // 重复值相对少
		v.push_back(i); // 没有重复，有序
	}

	size_t begin1 = clock();
	for (auto e : v) 
		s.insert(e);
	size_t end1 = clock();
	cout << "set insert:" << end1 - begin1 << endl;

	size_t begin2 = clock();
	for (auto e : v) 
		us.insert(e);
	size_t end2 = clock();
	cout << "unordered_set insert:" << end2 - begin2 << endl;


	size_t begin3 = clock();
	for (auto e : v) 
		s.find(e);
	size_t end3 = clock();
	cout << "set find:" << end3 - begin3 << endl;

	size_t begin4 = clock();
	for (auto e : v) 
		us.find(e);
	size_t end4 = clock();
	cout << "unordered_set find:" << end4 - begin4 << endl << endl;

	cout << "set插入数据个数：" << s.size() << endl;
	cout << "unordered_set插入数据个数：" << us.size() << endl << endl;

	size_t begin5 = clock();
	for (auto e : v) 
		s.erase(e);
	size_t end5 = clock();
	cout << "set erase:" << end5 - begin5 << endl;

	size_t begin6 = clock();
	for (auto e : v) 
		us.erase(e);
	size_t end6 = clock();
	cout << "unordered_set erase:" << end6 - begin6 << endl << endl;

	return 0;
}

第二章：底层结构

unordered系列的关联式容器之所以效率比较高，是因为其底层使用了哈希结构。

2.1 哈希概念

顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即O(log₂N)，搜索的效率取决于搜索过程中元素的比较次数。

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素。

当向该结构中：
插入元素
根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放

搜索元素
对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功

该方式即为哈希(散列)方法，哈希方法中使用的转换函数称为哈希(散列)函数，构造出来的结构称为哈希表(Hash Table)(或者称散列表)

例如：数据集合{1，7，6，4，5，9}；
哈希函数设置为：hash(key) = key % capacity; capacity为存储元素底层空间总的大小。

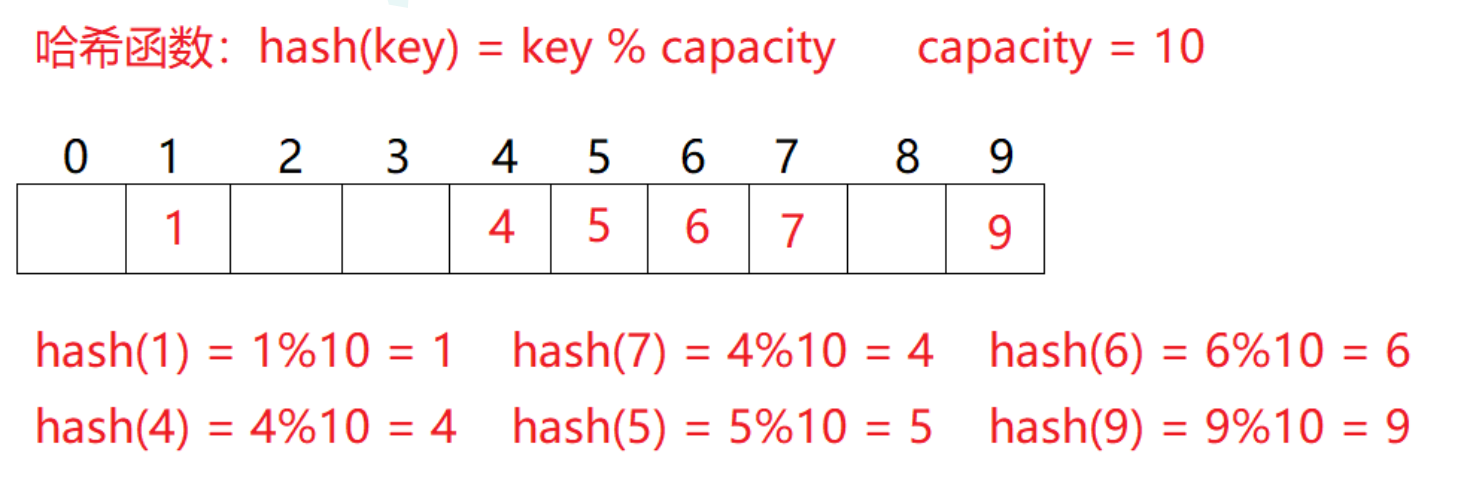
用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快
问题：按照上述哈希方式，向集合中插入元素44，会出现什么问题？

2.2 哈希冲突

对于两个数据元素的关键字$k_i$和 $k_j$(i != j)，有$k_i$ != $k_j$，但有：Hash($k_i$) == Hash($k_j$)，即：不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。

把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。

发生哈希冲突该如何处理呢？

2.3 哈希函数

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。
哈希函数设计原则：

• 哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域必须在0到m-1之间
• 哈希函数计算出来的地址能均匀分布在整个空间中
• 哈希函数应该比较简单

常见哈希函数

1. 直接定址法--(常用)

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
使用场景：适合查找比较小且连续的情况

2. 除留余数法--(常用)

设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：Hash(key) = key % p(p<=m),将关键码转换成哈希地址

3. 平方取中法--(了解)

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况

4. 折叠法--(了解)

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况

5. 随机数法--(了解)

选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random为随机数函数。
通常应用于关键字长度不等时采用此法

6. 数学分析法--(了解)

设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散列地址。例如：

假设要存储某家公司员工登记表，如果用手机号作为关键字，那么极有可能前7位都是 相同的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取工作还容易出现冲突，还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法。

数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布较均匀的情况

注意：哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突

2.4 哈希冲突解决

解决哈希冲突两种常见的方法是：闭散列和开散列

2.4.1 闭散列

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢？

1. 线性探测

比如下图中的场景，现在需要插入元素44，先通过哈希函数计算哈希地址，hashAddr为4，因此44理论上应该插在该位置，但是该位置已经放了值为4的元素，即发生哈希冲突。
线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。

插入
通过哈希函数获取待插入元素在哈希表中的位置
如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突，使用线性探测找到下一个空位置，插入新元素

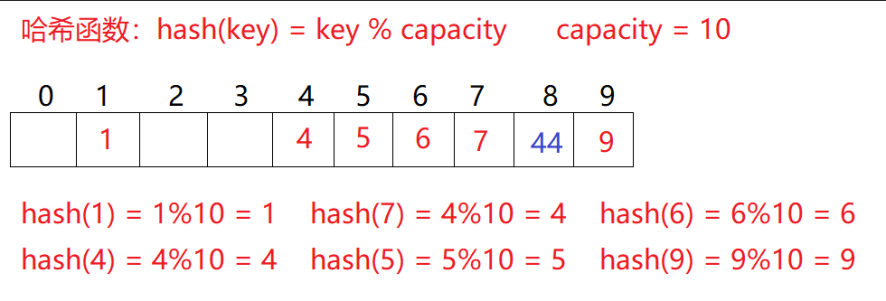
删除
采用闭散列处理哈希冲突时，不能随便物理删除哈希表中已有的元素，若直接删除元素会影响其他元素的搜索。比如删除元素4，如果直接删除掉，44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。

线性探测的实现

HashTable.h

#pragma once

//主模板 HashFunc<K> 提供默认行为，适用于可以直接转换为 size_t 的类型（如 int、long、char 等）。
template <class K>
struct HashFunc {
	size_t operator()(const K& key) { return (size_t)key; }
};

//特化版本 HashFunc<string> 针对 string 类型，提供更合理的哈希计算方式（BKDR Hash）。
template <>
struct HashFunc<string> {
	size_t operator()(const string& key) {
		size_t hash = 0;
		for (auto e : key) {
			hash *= 31;//为了解决"abc" "acb"结果相同(BKDR)
			hash += e;
		}
		return hash;//返回string中所有字符ASCII码值相加		
	}
};
//标准库中的unordered_map并不需要手动传第三个参数就可以处理string
//因为使用的是模版特化
//struct HashFuncString {
//	size_t operator()(const string& key) { 
//		size_t hash = 0;
//		for (auto e : key) {
//			hash *= 31;//为了解决"abc" "acb"结果相同(BKDR)
//			hash += e;
//		}			
//		return hash;//返回string中所有字符ASCII码值相加		
//	}
//};

//闭散列 / 开放定址法
namespace open_address {
	enum Status {
		EMPTY,
		EXIST,
		DELETE
	};

	template <class K, class V>
	struct HashData {
		pair<K, V> _kv;
		Status _s;
	};

	//如果key是string无法直接取模映射，所以需要仿函数
	//由于有些key(例如int)可以直接取模，所以仿函数设置为缺省参数
	template <class K, class V, class Hash = HashFunc<K>>
	class HashTable {
	public:
		HashTable() {
			_tables.resize(10);
		}
		bool Insert(const pair<K, V>& kv) {
			//不允许重复值。所以插入前先查找，如果找到就退出。
			if (Find(kv.first)) return false;

			//负载因子太大，冲突剧增，效率降低
			//负载因子太小，冲突降低，空间利用率低
			//if (_n / _tables.size() == 0.7) { //_n和_tables.size()都是无符号整数，相除不会得到浮点数
			if (_n * 10 / _tables.size() == 7) { //两边同时乘10
				//size_t newSize = _tables.size() * 2;
				//_tables.resize(newSize);
				//数据的位置要模_tables.size()，直接扩2倍导致数据的映射关系发生变化

				//扩容需要三步：
				//开新空间、重新映射、释放旧空间
				size_t newSize = _tables.size() * 2;
				HashTable<K, V, Hash> newHT;//创建新表
				newHT._tables.resize(newSize);//新表开空间是原表2倍
				for (size_t i = 0; i < _tables.size(); i++)//将原表的数据插入到新表
					if (_tables[i]._s == EXIST)
						newHT.Insert(_tables[i]._kv);
				_tables.swap(newHT._tables);
				//这里不用手动释放。因为newHT是这个if条件里的局部对象，出了作用域调用析构函数。
				//且HashTable没有写析构函数，自动生成的析构函数对自定义类型调用它的析构函数(即vector的析构函数)
			}
			//线性探测
			Hash hf;
			//只能模size是因为vector的operator[]只能访问[0, size())范围内的元素
			size_t hashi = hf(kv.first) % _tables.size();//如果key是string无法直接取模，所以需要仿函数
			while (_tables[hashi]._s == EXIST) { //如果hashi位置状态为存在
				++hashi;//向后移动
				hashi %= _tables.size();//为防止越界，需要取模。
			}
			_tables[hashi]._kv = kv;
			_tables[hashi]._s = EXIST;
			++_n;
			return true;
		}

		HashData<K, V>* Find(const K& key) {
			Hash hf;
			size_t hashi = hf(key) % _tables.size();
			//因为线性探测的冲突解决规则，导致相同哈希值的数据会聚集在一起，
			//所以 Find 在遇到 DELETE 状态时必须继续向后查找
			//而下方Erase是伪删除法，只是将状态置为DELETE，但数据还在，所以删除后，Find去查找，依然能找到
			while (_tables[hashi]._s != EMPTY) { //只要不是EMPTY就继续找（包括DELETE和EXIST）
				//if (_tables[hashi]._kv.first == key) //这样会导致删除的元素仍能被找到
				if (_tables[hashi]._s == EXIST
					&& _tables[hashi]._kv.first == key)//只有EXIST且key匹配才算找到
					return &_tables[hashi];
				++hashi;
				hashi %= _tables.size();
			}
			return nullptr;
		}

		bool Erase(const K& key) {
			HashData<K, V>* ret = Find(key);
			if (ret) {
				ret->_s = DELETE;
				--_n;
				return true;
			}
			else
				return false;
		}

		void Print() {
			for (size_t i = 0; i < _tables.size(); i++) {
				if (_tables[i]._s == EXIST)
					//printf("[%d]->%d\n", i, _tables[i]._kv.first);//只能打印key是int类型
					cout << "[" << i << "]->" << _tables[i]._kv.first << ":" << _tables[i]._kv.second << endl;
				else if (_tables[i]._s == EMPTY)
					printf("[%d]->\n", i);
				else
					printf("[%d]->D\n", i);
			}
			cout << endl;
		}
	private:
		vector<HashData<K, V>> _tables;
		size_t _n = 0;//存储的关键字的个数
		//1.如何判断某个位置是否储存了值
		//2.由于Find遇到空才停止，如果删除了某个值，怎么Find它后面的值
		//不能全找，这样就不符合哈希表查找的效率
		//所以每个位置需要标记状态
	};

	void TestHT1() {
		HashTable<int, int> ht;
		int a[] = { 4,14,24,34,5,7,1 };
		for (auto e : a)
			ht.Insert(make_pair(e, e));
		ht.Insert(make_pair(3, 3));
		ht.Insert(make_pair(3, 3));
		ht.Insert(make_pair(-3, -3));
		//插入负数没影响，因为映射时取模size是无符号数
		//负数整形会提升为无符号数
		ht.Print();

		ht.Erase(3);
		ht.Print();

		ht.Insert(make_pair(3, 3));
		ht.Insert(make_pair(23, 3));
		ht.Print();
	}

	void TestHT2() {
		string arr[] = { "香蕉", "甜瓜", "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
		HashTable<string, int> ht;
		for (auto& e : arr) {
			HashData<string, int>* ret = ht.Find(e);
			if (ret) ret->_kv.second++;
			else ht.Insert(make_pair(e, 1));
		}
		ht.Print();
	}
}

思考：哈希表什么情况下进行扩容？如何扩容？

线性探测优点：实现非常简单
线性探测缺点：一旦发生哈希冲突，所有的冲突连在一起，容易产生数据“堆积”，即：不同关键码占据了可利用的空位置，使得寻找某关键码的位置需要许多次比较，导致搜索效率降低。如何缓解呢？

2. 二次探测

线性探测的缺陷是产生冲突的数据堆积在一块，这与其找下一个空位置有关系，因为找空位置的方式就是挨着往后逐个去找，因此二次探测为了避免该问题，找下一个空位置的方法为：$H_i$ = ($H_0$ + $i^2$ )% m, 或者：$H_i$ = ($H_0$ - $i^2$ )% m。其中：i = 1,2,3…， $H_0$是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置，m是表的大小。

研究表明：当表的长度为质数且表装载因子a不超过0.5时，新的表项一定能够插入，而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置，就不会存在表满的问题。在搜索时可以不考虑表装满的情况，但在插入时必须确保表的装载因子a不超过0.5，如果超出必须考虑增容。

因此：闭散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷。

2.4.2 开散列

1. 开散列概念

开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

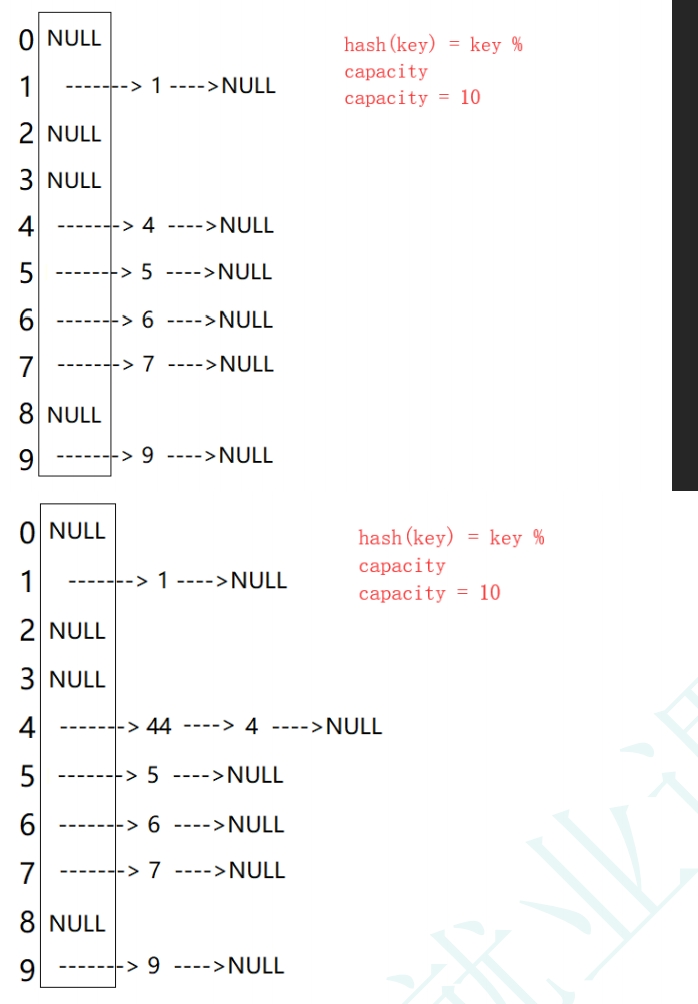
从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。

2. 开散列实现

HashTable.h

namespace hash_bucket {
	//template <class K, class V>
	//struct HashNode {

	//};
	//template <class K, class V>
	//class HashTable {
	//	typedef HashNode<K, V> Node;
	//private:
	//	//如果只为了实现哈希表，用这个
	//	//struct bucket {
	//	//	forward_list<pair<K, V>> _lt;
	//	//	set<pair<K, V>> _rbtree;
	//	//	size_t len = 0;//超过8改为红黑树
	//	//};
	//	//vector<bucket> _tables;//不选择这种方式是因为需要自己实现迭代器

	//	vector<Node*> _tables;
	//	size_t _n = 0;
	//};

	template <class K, class V>
	struct HashNode {
		HashNode* _next;
		pair<K, V> _kv;

		HashNode(const pair<K, V>& kv)
			:_next(nullptr)
			, _kv(kv) {
		}
	};
	template <class K, class V, class Hash = HashFunc<K>>
	class HashTable {
		typedef HashNode<K, V> Node;
	public:
		//vector<Node*> 调用 resize(10) 后，所有指针会被默认初始化为 nullptr
		//（因为 Node* 是内置指针类型，默认初始化是未定义的，但 resize 会进行值初始化，即 nullptr）。
		HashTable() { _tables.resize(10, nullptr); }

		//因为哈希桶的vector每个位置的数据是一串链表
		//自动生成的析构只会释放vector，所以需要自己实现析构去释放链表
		~HashTable() {
			for (size_t i = 0; i < _tables.size(); i++) {
				Node* cur = _tables[i];
				while (cur) {
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

		bool Insert(const pair<K, V>& kv) {
			if (Find(kv.first)) return false;//不允许重复key
			Hash hf;
			//哈希桶不扩容不会死循环，但每个桶装太多数据效率低
			//哈希桶负载因子最大是1
			//if (_n == _tables.size()) {
			//	//如果使用闭散列的逻辑会有问题，开散列的哈希表每个位置是一个哈希桶(即链表)
			//	//重新创建新链表，释放就链表消耗很大
			//	size_t newSize = _tables.size() * 2;
			//	HashTable<K, V> newHT;
			//	newHT._tables.resize(newSize);
			//	for (size_t i = 0; i < _tables.size(); i++) {
			//		Node* cur = _tables[i];
			//		while (cur) {
			//			newHT.Insert(cur->_kv);
			//			cur = cur->_next;
			//		}
			//	}
			//	_tables.swap(newHT._tables);
			//}
			if (_n == _tables.size()) {
				vector<Node*> newTables;
				newTables.resize(_tables.size() * 2, nullptr);
				for (size_t i = 0; i < _tables.size(); i++) {
					Node* cur = _tables[i];
					while (cur) {
						Node* next = cur->_next;
						size_t hashi = hf(cur->_kv.first) % newTables.size();
						cur->_next = newTables[hashi];
						newTables[hashi] = cur;
						cur = next;
					}
					_tables[i] = nullptr;//旧表中i的位置依然指向新表，如果不置空，析构会有问题
				}
				_tables.swap(newTables);
				//让 _tables 指向扩容后的新表。
				//让 newTables 接管旧表，通过析构自动释放内存。
			}
			size_t hashi = hf(kv.first) % _tables.size();//key映射到哈希表的位置
			Node* newnode = new Node(kv);
			//头插
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;
			return true;
		}

		Node* Find(const K& key) {
			Hash hf;
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur) {
				if (cur->_kv.first == key)
					return cur;
				cur = cur->_next;
			}
			return nullptr;
		}

		bool Erase(const K& key) {
			Hash hf;
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			Node* prev = nullptr;
			while (cur) { //遍历哈希桶
				if (cur->_kv.first == key) { //如果找到了
					if (prev == nullptr) //且是第一个
						_tables[hashi] = cur->_next;
					else
						prev->_next = cur->_next;
					delete cur;
					return true;
				}
				prev = cur;
				cur = cur->_next;
			}
			return false;
		}

		void Some() {
			size_t bucketSize = 0;//有多少个桶
			size_t maxBucketLen = 0;//单个桶最大长度
			size_t sum = 0;//元素总数
			double averageBucketLen = 0;//平均桶长度
			for (size_t i = 0; i < _tables.size(); i++) {
				Node* cur = _tables[i];
				if (cur) ++bucketSize;
				size_t bucketLen = 0;//单个桶长度
				while (cur) {
					++bucketLen;
					cur = cur->_next;
				}
				sum += bucketLen;
				if (bucketLen > maxBucketLen) maxBucketLen = bucketLen;
			}
			averageBucketLen = (double)sum / (double)bucketSize;
			cout << "all bucketSize:" << _tables.size() << endl;
			cout << "bucketSize:" << bucketSize << endl;
			cout << "maxBucketLen:" << maxBucketLen << endl;
			cout << "averageBucketLen:" << averageBucketLen << endl;
			cout << endl;
		}
	private:
		vector<Node*> _tables;
		size_t _n = 0;
	};

	void TestHT1() {
		HashTable<int, int> ht;
		int a[] = { 4,14,24,34,5,7,1,15,25,3 };
		for (auto e : a)
			ht.Insert(make_pair(e, e));
		ht.Insert(make_pair(13, 13));
		cout << ht.Find(4) << endl;
		ht.Erase(4);
		cout << ht.Find(4) << endl;
	}

	void TestHT2() {
		string arr[] = { "香蕉", "甜瓜", "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
		HashTable<string, int> ht;
		for (auto& e : arr) {
			HashNode<string, int>* ret = ht.Find(e);
			if (ret) ret->_kv.second++;
			else ht.Insert(make_pair(e, 1));
		}
	}

	void TestHT3() {
		const size_t N = 1000000;

		unordered_set<int> us;
		set<int> s;
		HashTable<int, int> ht;

		vector<int> v;
		v.reserve(N);
		srand((size_t)time(0));
		for (size_t i = 0; i < N; ++i) {
			//v.push_back(rand()); // N比较大时，重复值比较多
			v.push_back(rand() + i); // 重复值相对少
			//v.push_back(i); // 没有重复，有序
		}

		size_t begin1 = clock();
		for (auto e : v)
			s.insert(e);
		size_t end1 = clock();
		cout << "set insert:" << end1 - begin1 << endl;

		size_t begin2 = clock();
		for (auto e : v)
			us.insert(e);
		size_t end2 = clock();
		cout << "unordered_set insert:" << end2 - begin2 << endl;

		size_t begin10 = clock();
		for (auto e : v)
			ht.Insert(make_pair(e, e));
		size_t end10 = clock();
		cout << "HashTable insert:" << end10 - begin10 << endl << endl;


		size_t begin3 = clock();
		for (auto e : v)
			s.find(e);
		size_t end3 = clock();
		cout << "set find:" << end3 - begin3 << endl;

		size_t begin4 = clock();
		for (auto e : v)
			us.find(e);
		size_t end4 = clock();
		cout << "unordered_set find:" << end4 - begin4 << endl;

		size_t begin11 = clock();
		for (auto e : v)
			ht.Find(e);
		size_t end11 = clock();
		cout << "HashTable find:" << end11 - begin11 << endl << endl;

		cout << "插入数据个数：" << s.size() << endl;
		ht.Some();

		size_t begin5 = clock();
		for (auto e : v)
			s.erase(e);
		size_t end5 = clock();
		cout << "set erase:" << end5 - begin5 << endl;

		size_t begin6 = clock();
		for (auto e : v)
			us.erase(e);
		size_t end6 = clock();
		cout << "unordered_set erase:" << end6 - begin6 << endl;

		size_t begin12 = clock();
		for (auto e : v)
			ht.Erase(e);
		size_t end12 = clock();
		cout << "HashTable erase:" << end12 - begin12 << endl;
	}
}

3. 开散列增容

桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可能会导致一个桶中链表节点非常多，会影响哈希表的性能，因此在一定条件下需要对哈希表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可以给哈希表增容。

4. 开散列的思考

1. 只能存储key为整形的元素，其他类型怎么解决？
2. 除留余数法，最好模一个素数，如何每次快速取一个类似两倍关系的素数？

5. 开散列与闭散列比较

应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上：由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <= 0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。

第三章：模拟实现

MyUnorderedSet.h

#pragma once
#include "HashTable.h"

namespace bit {
	template <class K, class Hash = HashFunc<K>>
	class unordered_set {
		struct SetKeyOfT {
			const K& operator() (const K& key) { return key; }
		};
	public:
		typedef typename hash_bucket::HashTable<K, K, SetKeyOfT, Hash>::const_iterator iterator;
		typedef typename hash_bucket::HashTable<K, K, SetKeyOfT, Hash>::const_iterator const_iterator;
		//iterator begin() { return _ht.begin(); }
		//iterator end() { return _ht.end(); }

		//begin() const 和 end() const 是为了支持 const unordered_set 对象
		const_iterator begin() const { return _ht.begin(); }
		const_iterator end() const { return _ht.end(); }
		//unordered_set的iterator和const_iterator是同一个类型，即 HashTable::const_iterator。
		//但 HashTable::Insert返回的是一个pair<iterator, bool>，其中iterator是HashTable::iterator（非 const 版本）。
		//通过显式构造一个const_iterator，将ret.first（HashTable::iterator）的成员（_node、_pht、_hashi）传递给const_iterator的构造函数。
		pair<iterator, bool> insert(const K& key) {
			auto ret = _ht.Insert(key);
			return pair<iterator, bool>(iterator(ret.first._node, ret.first._pht, ret.first._hashi), ret.second);
		}

		iterator find(const K& key) { return _ht.Find(key); }
		bool erase(const K& key) { return _ht.Erase(key); }
	private:
		hash_bucket::HashTable<K, K, SetKeyOfT, Hash> _ht;
	};

	void test_set() {
		unordered_set<int> us;
		us.insert(5);
		us.insert(15);
		us.insert(52);
		us.insert(3);
		unordered_set<int>::iterator it = us.begin();
		while (it != us.end()) {
			cout << *it << " ";
			++it;
		}
		cout << endl;

		for (auto e : us)
			cout << e << " ";
		cout << endl;
	}
}

MyUnorderedMap.h

#pragma once
#include "HashTable.h"

namespace bit {
	template <class K, class V, class Hash = HashFunc<K>>
	class unordered_map {
		struct MapKeyOfT {
			const K& operator() (const pair<K, V>& kv) { return kv.first; }
		};
	public:
		typedef typename hash_bucket::HashTable<K, pair<const K, V>, MapKeyOfT, Hash>::iterator iterator;
		typedef typename hash_bucket::HashTable<K, pair<const K, V>, MapKeyOfT, Hash>::const_iterator const_iterator;
		iterator begin() { return _ht.begin(); }
		iterator end() { return _ht.end(); }
		const_iterator begin() const { return _ht.begin(); }
		const_iterator end() const { return _ht.end(); }
		pair<iterator, bool> insert(const pair<K, V>& kv) { return _ht.Insert(kv); }
		V& operator[](const K& key) {
			pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));
			return ret.first->second;
		}
		const V& operator[](const K& key) const {
			pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));
			return ret.first->second;
		}

		iterator find(const K& key) { return _ht.Find(key); }
		bool erase(const K& key) { return _ht.Erase(key); }

	private:
		hash_bucket::HashTable<K, pair<const K, V>, MapKeyOfT, Hash> _ht;
	};

	void test_map() {
		unordered_map<string, string> dict;
		dict.insert(make_pair("sort", "排序"));
		dict.insert(make_pair("string", "字符串"));
		dict.insert(make_pair("insert", "插入"));
		for (auto& kv : dict) {
			//kv.first += 'x';
			//kv.second += 'x';
			cout << kv.first << ":" << kv.second << endl;
		}
		cout << endl;

		string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
		unordered_map<string, int> countMap;
		for (auto& e : arr)
			countMap[e]++;

		for (auto& kv : countMap)
			cout << kv.first << ":" << kv.second << endl;
	}
}

HashTable.h

#pragma once

//主模板 HashFunc<K> 提供默认行为，适用于可以直接转换为 size_t 的类型（如 int、long、char 等）。
template <class K>
struct HashFunc {
	size_t operator()(const K& key) { return (size_t)key; }
};

//特化版本 HashFunc<string> 针对 string 类型，提供更合理的哈希计算方式（BKDR Hash）。
template <>
struct HashFunc<string> {
	size_t operator()(const string& key) {
		size_t hash = 0;
		for (auto e : key) {
			hash *= 31;//为了解决"abc" "acb"结果相同(BKDR)
			hash += e;
		}
		return hash;//返回string中所有字符ASCII码值相加		
	}
};
//标准库中的unordered_map并不需要手动传第三个参数就可以处理string
//因为使用的是模版特化
//struct HashFuncString {
//	size_t operator()(const string& key) { 
//		size_t hash = 0;
//		for (auto e : key) {
//			hash *= 31;//为了解决"abc" "acb"结果相同(BKDR)
//			hash += e;
//		}			
//		return hash;//返回string中所有字符ASCII码值相加		
//	}
//};

//开散列 / 链地址法(开链法)
namespace hash_bucket {
	//template <class K, class V>
	template <class T>//类似红黑树，改为泛型。不管什么数据类型都用T接收
	struct HashNode {
		HashNode<T>* _next;
		T _data;

		HashNode(const T& data)
			:_next(nullptr)
			, _data(data) {
		}
	};

	//为解决迭代器要用哈希表，哈希表在下面找不到。使用前置声明(不要缺省参数)
	template <class K, class T, class KeyOfT, class Hash>
	class HashTable;

	template <class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>
	struct __HTIterator {
		typedef HashNode<T> Node;
		typedef __HTIterator<K, T, Ref, Ptr, KeyOfT, Hash> Self;
		Node* _node;
		//迭代器要用哈希表，哈希表在下面找不到
		const HashTable<K, T, KeyOfT, Hash>* _pht;
		//vector<Node*>* _pf;//这种方式也可以解决前后依赖

		size_t _hashi;//方法二：直接给出

		__HTIterator(Node* node, HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi)
			:_node(node), _pht(pht), _hashi(hashi) {
		}

		//这个用于构造const迭代器。const迭代器有const修饰this(即有const修饰的this指向哈希表)
		__HTIterator(Node* node, const HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi)
			:_node(node), _pht(pht), _hashi(hashi) {
		}

		Self& operator++() {
			//begin()的实现确保返回第一个有效桶，所以可以直接判断
			if (_node->_next) {
				//当前桶还有节点，找下一个节点
				_node = _node->_next;
			}
			else {
				//当前桶遍历完，找下一个不为空的桶。
				//找下一个桶需要HashTable 或 vector<Node*>
				//方法一：现算hashi
				//Hash hf;
				//KeyOfT kot;
				//size_t hashi = hf(kot(_node->_data)) % _pht->_tables.size();
				++_hashi;
				while (_hashi < _pht->_tables.size()) { //_tables是HashTable的私有成员，访问不了
					if (_pht->_tables[_hashi]) { //如果有桶
						_node = _pht->_tables[_hashi];//_node从这开始遍历
						break;
					}
					++_hashi;
				}
				if (_hashi == _pht->_tables.size()) _node = nullptr;//遍历完哈希表
			}
			return *this;
		}

		bool operator!=(const Self& s) { return _node != s._node; }
		Ref operator*() { return _node->_data; }
		Ptr operator->() { return &_node->_data; }
	};

	//unordered_set -> HashTable<K, K>
	//unordered_set -> HashTable<K, pair<K, V>>
	template <class K, class T, class KeyOfT, class Hash>
	class HashTable {
		typedef HashNode<T> Node;
		//为了迭代器能访问HashTable的私有成员_tables，做类模板的友元声明
		template <class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>
		friend struct __HTIterator;
	public:
		typedef __HTIterator<K, T, T&, T*, KeyOfT, Hash> iterator;
		typedef __HTIterator<K, T, const T&, const T*, KeyOfT, Hash> const_iterator;
		iterator begin() {
			for (size_t i = 0; i < _tables.size(); i++)
				if (_tables[i])
					return iterator(_tables[i], this, i);
			return end();
		}
		iterator end() { return iterator(nullptr, this, -1); }

		//this -> const HashTable<K, T, KeyOfT, Hash>*
		//这里的this是const修饰的，但迭代器的构造函数中使用的参数是非const
		//const不能传给非const
		const_iterator begin() const {
			for (size_t i = 0; i < _tables.size(); i++)
				if (_tables[i])
					return const_iterator(_tables[i], this, i);
			return end();
		}
		const_iterator end() const { return const_iterator(nullptr, this, -1); }

		//vector<Node*> 调用 resize(10) 后，所有指针会被默认初始化为 nullptr
		//（因为 Node* 是内置指针类型，默认初始化是未定义的，但 resize 会进行值初始化，即 nullptr）。
		HashTable() { _tables.resize(10, nullptr); }

		//因为哈希桶的vector每个位置的数据是一串链表
		//自动生成的析构只会释放vector，所以需要自己实现析构去释放链表
		~HashTable() {
			for (size_t i = 0; i < _tables.size(); i++) {
				Node* cur = _tables[i];
				while (cur) {
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

		pair<iterator, bool> Insert(const T& data) {
			Hash hf;
			KeyOfT kot;
			iterator it = Find(kot(data));
			if (it != end()) return make_pair(it, false);//不允许重复key

			if (_n == _tables.size()) {
				vector<Node*> newTables;
				newTables.resize(_tables.size() * 2, nullptr);
				for (size_t i = 0; i < _tables.size(); i++) {
					Node* cur = _tables[i];
					while (cur) {
						Node* next = cur->_next;
						//hf是将数据转换为size_t；kot是取数据的key的值
						size_t hashi = hf(kot(cur->_data)) % newTables.size();
						cur->_next = newTables[hashi];
						newTables[hashi] = cur;
						cur = next;
					}
					_tables[i] = nullptr;//旧表中i的位置依然指向新表，如果不置空，析构会有问题
				}
				_tables.swap(newTables);
				//让 _tables 指向扩容后的新表。
				//让 newTables 接管旧表，通过析构自动释放内存。
			}
			size_t hashi = hf(kot(data)) % _tables.size();//key映射到哈希表的位置
			Node* newnode = new Node(data);
			//头插
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;
			return make_pair(iterator(newnode, this, hashi), true);
		}

		iterator Find(const K& key) {
			Hash hf;
			KeyOfT kot;
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur) {
				if (kot(cur->_data) == key)
					return iterator(cur, this, hashi);
				cur = cur->_next;
			}
			return end();
		}

		bool Erase(const K& key) {
			Hash hf;
			KeyOfT kot;
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			Node* prev = nullptr;
			while (cur) { //遍历哈希桶
				if (kot(cur->_data) == key) { //如果找到了
					if (prev == nullptr) //且是第一个
						_tables[hashi] = cur->_next;
					else
						prev->_next = cur->_next;
					delete cur;
					return true;
				}
				prev = cur;
				cur = cur->_next;
			}
			return false;
		}

		void Some() {
			size_t bucketSize = 0;//有多少个桶
			size_t maxBucketLen = 0;//单个桶最大长度
			size_t sum = 0;//元素总数
			double averageBucketLen = 0;//平均桶长度
			for (size_t i = 0; i < _tables.size(); i++) {
				Node* cur = _tables[i];
				if (cur) ++bucketSize;
				size_t bucketLen = 0;//单个桶长度
				while (cur) {
					++bucketLen;
					cur = cur->_next;
				}
				sum += bucketLen;
				if (bucketLen > maxBucketLen) maxBucketLen = bucketLen;
			}
			averageBucketLen = (double)sum / (double)bucketSize;
			cout << "all bucketSize:" << _tables.size() << endl;
			cout << "bucketSize:" << bucketSize << endl;
			cout << "maxBucketLen:" << maxBucketLen << endl;
			cout << "averageBucketLen:" << averageBucketLen << endl;
			cout << endl;
		}
	private:
		vector<Node*> _tables;
		size_t _n = 0;
	};
}

第四章：哈希的应用

4.1 位图

4.1.1 位图概念

1. 面试题
给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

1. 遍历，时间复杂度O(N)
2. 排序(O(NlogN))，利用二分查找: logN
3. 位图解决

数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在。比如：

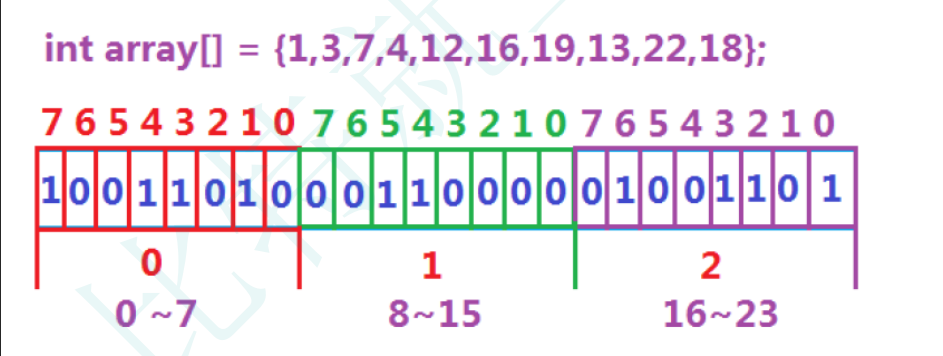
2. 位图概念
所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。 

4.1.2 位图的实现

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

//数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，
//那么可以使用一个二进制比特位来代表数据是否存在的信息，
//如果二进制比特位为1，代表存在，为0代表不存在
template <size_t N>//N是需要多少比特位
class bitset {
public:
	bitset() {
		//N如果不是32的倍数，N/32会舍去余数，所以多开一个整型
		_bits.resize(N / 32 + 1);
	}

	void set(size_t x) { //将某一个比特位置为1
		size_t i = x / 32;//找在第几个整型
		size_t j = x % 32;//找在该整形的第几位
		_bits[i] |= (1 << j);//左移是向高位移动
	}

	void reset(size_t x) { //将某一个比特位置为0
		size_t i = x / 32;
		size_t j = x % 32;
		_bits[i] &= ~(1 << j);
	}

	bool test(size_t x) { //检查某一个比特位是0或1
		size_t i = x / 32;
		size_t j = x % 32;
		return _bits[i] & (1 << j);
		//如果该位是0，那么结果是全0，所以是假
		//如果该位是1，那么结果不是全0，非0是真
	}
private:
	vector<int> _bits;
	//创建一个存储整型的vector，用每个比特位表示在或不在
};

给定100亿个整数，设计算法找到只出现一次的整数？

//用两个比特位来标记状态：00 - 出现0次；01 - 出现1次；10 - 出现2次及以上
//虽然有100亿个数据，但整形只有2^32次方个，所以只会在这2^32个中出现
//所以最多只需要开2^32个比特位就足够
template <size_t N>
class twobitset {
public:
	void set(size_t x) {
		//00->01; 01->10; 10->不变
		if (_bs1.test(x) == false && _bs2.test(x) == false)
			_bs2.set(x);
		else if (_bs1.test(x) == false && _bs2.test(x) == true) {
			_bs1.set(x);
			_bs2.reset(x);
		}
	}

	void PrintOnce() {
		for (size_t i = 0; i < N; i++)
			if (_bs1.test(i) == false && _bs2.test(i) == true)
				cout << i << " ";
		cout << endl;
	}
private:
	bitset<N> _bs1;
	bitset<N> _bs2;
	//复用上面两个位图上下对齐
	//即第一个位图的第1位
	//和第二个位图的第1位 组成状态标记
};

1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

//和第一题思路类似。00 - 出现0次；01 - 出现1次；10 - 出现2次；11 - 出现3次及以上
template <size_t N>
class nomoretwobitset {
public:
	void set(size_t x) {
		//00->01; 01->10; 10->11; 11-不变
		if (_bs1.test(x) == false && _bs2.test(x) == false)
			_bs2.set(x);
		else if (_bs1.test(x) == false && _bs2.test(x) == true) {
			_bs1.set(x);
			_bs2.reset(x);
		}
		else if (_bs1.test(x) == true && _bs2.test(x) == false) {
			_bs1.set(x);
			_bs2.set(x);
		}
	}

	void Print() {
		for (size_t i = 0; i < N; i++) {
			if (_bs1.test(i) == false && _bs2.test(i) == true)
				cout << "1->" << i << endl;
			else if (_bs1.test(i) == true && _bs2.test(i) == false)
				cout << "2->" << i << endl;
		}
		cout << endl;
	}
private:
	bitset<N> _bs1;
	bitset<N> _bs2;
	//复用上面两个位图上下对齐
	//即第一个位图的第1位
	//和第二个位图的第1位 组成状态标记
};

4.1.3 位图的应用

1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记

4.2 布隆过滤器

4.2.1 布隆过滤器提出

我们在使用新闻客户端看新闻时，它会给我们不停地推荐新的内容，它每次推荐时要去重，去掉那些已经看过的内容。问题来了，新闻客户端推荐系统如何实现推送去重的？ 用服务器记录了用户看过的所有历史记录，当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选，过滤掉那些已经存在的记录。 如何快速查找呢？

1. 用哈希表存储用户记录，缺点：浪费空间
2. 用位图存储用户记录，缺点：位图一般只能处理整形，如果内容编号是字符串，就无法处理了。
3. 将哈希与位图结合，即布隆过滤器

4.2.2布隆过滤器概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间。

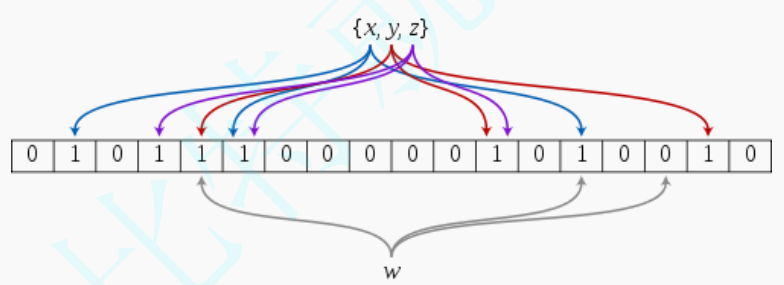
4.2.3 布隆过滤器的插入

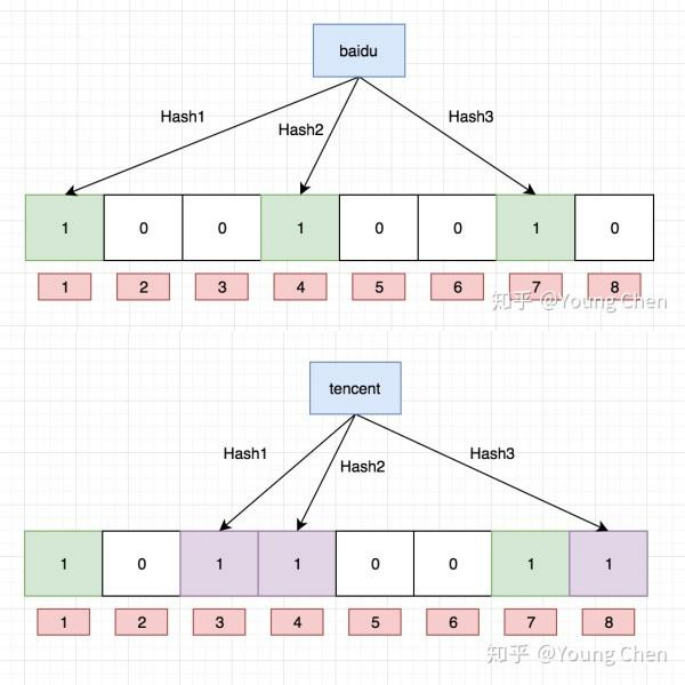
向布隆过滤器中插入："baidu"

Bloom Filter.h

#pragma once
#include <string>
#include <bitset>
#include <vector>
#include "Bitmap.h"

struct BKDRHash {
	size_t operator()(const string& key) {
		size_t hash = 0;
		for (auto e : key) {
			hash *= 31;//为了解决"abc" "acb"结果相同(BKDR)
			hash += e;
		}
		return hash;//返回string中所有字符ASCII码值相加		
	}
};

struct APHash {
	size_t operator()(const string& key) {
		size_t hash = 0;
		for (size_t i = 0; i < key.size(); i++) {
			char ch = key[i];
			if ((i & 1) == 0)
				hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
			else
				hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
		}
		return hash;
	}
};

struct DJBHash {
	size_t operator()(const string& key) {
		size_t hash = 5381;
		for (auto ch : key)
			hash += (hash << 5) + ch;
		return hash;
	}
};

template <size_t N, class K = string, class HashFunc1 = BKDRHash, class HashFunc2 = APHash, class HashFunc3 = DJBHash>
class BloomFilter {
public:
	void Set(const K& key) {
		//HashFunc1() 创建了一个该类型的临时匿名对象（调用了默认构造函数）
		//HashFunc1()(key) 对这个临时对象调用了 operator()，并传入 key 作为参数。
		size_t hash1 = HashFunc1()(key) % N;
		size_t hash2 = HashFunc2()(key) % N;
		size_t hash3 = HashFunc3()(key) % N;

		_bs.set(hash1);
		_bs.set(hash2);
		_bs.set(hash3);
	}

	bool Test(const K& key) {
		size_t hash1 = HashFunc1()(key) % N;
		if (_bs.test(hash1) == false) return false;
		size_t hash2 = HashFunc2()(key) % N;
		if (_bs.test(hash2) == false) return false;
		size_t hash3 = HashFunc3()(key) % N;
		if (_bs.test(hash3) == false) return false;

		return true;
	}

	//将数据映射的比特位置为0是不支持的
	//因为不同的数据可能映射到同一个比特位
	//想支持删除要使用引用计数，
	//即有几个数据映射到该位置就显示几，但数据多了一个比特位就不足以支持
	//用多个比特位标记一个值，存引用计数
	void Reset(const K& key);
private:
	bit::bitset<N> _bs;
};

4.2.4 布隆过滤器的查找

布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中，因此被映射到的位置的比特位一定为1。所以可以按照以下方式进行查找：分别计算每个哈希值对应的比特位置存储的是否为零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中。

注意：布隆过滤器如果说某个元素不存在时，该元素一定不存在，如果该元素存在时，该元素可能存在，因为有些哈希函数存在一定的误判。

比如：在布隆过滤器中查找"alibaba"时，假设3个哈希函数计算的哈希值为：1、3、7，刚好和其他元素的比特位重叠，此时布隆过滤器告诉该元素存在，但实该元素是不存在的。

4.2.5 布隆过滤器删除

布隆过滤器不能直接支持删除工作，因为在删除一个元素时，可能会影响其他元素。

比如：删除上图中"tencent"元素，如果直接将该元素所对应的二进制比特位置0，“baidu”元素也被删除了，因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。

一种支持删除的方法：将布隆过滤器中的每个比特位扩展成一个小的计数器，插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一，删除元素时，给k个计数器减一，通过多占用几倍存储空间的代价来增加删除操作。

缺陷：

1. 无法确认元素是否真正在布隆过滤器中
2. 存在计数回绕

4.2.6 布隆过滤器优点

1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无关
2. 哈希函数相互之间没有关系，方便硬件并行运算
3. 布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势
4. 在能够承受一定的误判时，布隆过滤器比其他数据结构有着很大的空间优势
5. 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算

4.2.7 布隆过滤器缺陷

1. 有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中(补救方法：再建立一个白名单，存储可能会误判的数据)
2. 不能获取元素本身
3. 一般情况下不能从布隆过滤器中删除元素
4. 如果采用计数方式删除，可能会存在计数回绕问题

第五章：海量数据面试题

5.1 哈希切割

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？

使用哈希表的思想。假设准备100个小文件，将IP地址转换为整型在取模映射到这些小文件中。这样相同的IP一定进入同一个小文件。再对小文件使用map统计IP次数。

5.2 布隆过滤器

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

近似算法：与上面题目思路相似。使用哈希表的思想，两份文件命名为A、B。假设准备500个小文件，读取query，将query转换为整型在取模映射到这些小文件中(计算 i = Hash(query) % 500, i是几，query就进入Ai小文件)。A被分割为A0~A499，B也如此。这样A和B中相同的query分别进入编号相同的小文件中。

Ai和Bi分别插入一个setA和setB，快速找交集。

如果某个小文件太大(10G)，无法加载到内存怎么办？

1. 这个小文件中大多数都是某个query
2. 这个小文件有很多不同的query

不管文件大小，直接读取到内存中并插入set。

如果是情况1，文件很大且有很多重复，后面重复数据插入失败，所以能够插入到set中。

如果是情况2，不断插入set后，内存不足会抛异常，需要换一个哈希函数进行二次切分，再找交集

作业

1. 关于map和unordered_map说法不正确的是（）

A.它们中都存储的键值对
B.map适合key有序的场景，unordered_map没有有序的要求
C.它们中元素查找的方式相同
D.map的底层结构是红黑树，unordered_map的底层结构是哈希桶

答案：C
A：正确，结合文档说明
B：正确，因为map的底层是红黑树，红黑树中序遍历可以得到关于key有序的序列，而unordered_map底层是哈希桶，哈希对于其存储的元素是否有序，并不关心
C：错误，map按照二叉搜索树的规则查找，unordered_map按照哈希方式进行查找
D：正确

2. 关于unordered_map和unordered_set说法错误的是（）

A.它们中存储元素的类型不同，unordered_map存储键值对，而unordered_set中只存储key
B.它们的底层结构相同，都使用哈希桶
C.它们查找的时间复杂度平均都是O(1)
D.它们在进行元素插入时，都得要通过key的比较去找待插入元素的位置

答案：D
A：正确，参考unordered_map和unordered_set的文档说明
B：正确，都采用的是哈希桶来实现的
C：正确，哈希是通过哈希函数来计算元素的存储位置的，找的时候同样通过哈希函数找元素位置，不需要循环遍历因此时间复杂度为O(1)
D：错误，不需要比较，只需要通过哈希函数，就可以确认元素需要存储的位置

3. 两句话中的不常见单词 884. 两句话中的不常见单词 - 力扣（LeetCode）

class Solution {
public:
    vector<string> uncommonFromSentences(string s1, string s2) {
        unordered_map<string, int> um;
        string ret;
        //统计s1中单词的次数
        for (int i = 0; i < s1.size(); ++i) {
            if (s1[i] == ' ') { // 遇到空，将单词插入unordered_map并更新统计次数
                um[ret]++;
                ret = ""; // 插入unordered_map后，将单词string置空
            } else        // 不为空，将字符追加到string ret
                ret += s1[i];
        }
        um[ret]++; // 循环结束后，将最后一个单词插入
        ret = "";

        //统计s2中单词的次数
        for (int i = 0; i < s2.size(); ++i) {
            if (s2[i] == ' ') { // 遇到空，将单词插入unordered_map并更新统计次数
                um[ret]++;
                ret = ""; // 插入unordered_map后，将单词string置空
            } else        // 不为空，将字符追加到string ret
                ret += s2[i];
        }
        um[ret]++; // 循环结束后，将最后一个单词插入
        ret = "";

        //遍历unordered_map，将value是1的插入到vector中
        vector<string> v;
        auto it = um.begin();
        while (it != um.end()) {
            if (it->second == 1)
                v.push_back(it->first);
            ++it;
        }
        return v;
    }
};

4. 存在重复元素 217. 存在重复元素 - 力扣（LeetCode）

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        //方法一
        unordered_map<int, int> um;
        for (auto e : nums)
            um[e]++;

        auto it = um.begin();
        while (it != um.end()){
            if (it->second >= 2)
                return true;
            ++it;
        }
        return false;

        // 方法二
        unordered_set<int> us;
        for(auto e : nums){
            //找不到返回end()，e还没插入就找不到
            //end != end为假，所以直接插入
            if (us.find(e) != us.end())
                return true;
            us.insert(e);
        }
        return false;
    }
};

5. 两个数组的交集2 350. 两个数组的交集 II - 力扣（LeetCode）

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        multiset<int> map1(nums1.begin(), nums1.end());
        multiset<int> map2(nums2.begin(), nums2.end());
        multiset<int>:: iterator it1 = map1.begin();
        auto it2 = map2.begin();
        vector<int> v;
        while (it1 != map1.end() && it2 != map2.end()) {
            if (*it1 < *it2) 
                ++it1;
            else if (*it2 < *it1)
                ++it2;               
            else{
                v.push_back(*it1);
                ++it1;
                ++it2;
            }
        }
        return v;
    }
};

6. 两个数组的交集1 349. 两个数组的交集 - 力扣（LeetCode）

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        //一个vector的数据插入到set中，用另一个vector的元素来查找不可以行
        //因为两个vector中都可能会有重复数据
        //nums1 = [1,2,2,1], nums2 = [2,2]
        //如果用nums2里的两个2去set中查找都会有，无法判断

        //set可以排序+去重
        set<int> map1(nums1.begin(), nums1.end());
        set<int> map2(nums2.begin(), nums2.end());

        //找交集 - 双指针
        //set1：4 5 8    set2：4 8 9
        //1.相同就是交集值，同时++
        //2.不相同，小的++。因为排过序，小的不会和另一个map后面的值相同
        //有一个结束就结束

        //找差集
        //1.相同，同时++
        //2.不相同，小的++。小的是差集，因为排过序，小的不会和另一个map后面的值相同
        //一个结束，另一个是差集
        set<int>:: iterator it1 = map1.begin();
        auto it2 = map2.begin();
        vector<int> v;
        while (it1 != map1.end() && it2 != map2.end()) {
            if (*it1 < *it2) 
                ++it1;
            else if (*it2 < *it1)
                ++it2;               
            else{
                v.push_back(*it1);
                ++it1;
                ++it2;
            }
        }
        return v;
    }
};

7. 重复 N 次的元素 961. 在长度 2N 的数组中找出重复 N 次的元素 - 力扣（LeetCode）

class Solution {
public:
    int repeatedNTimes(vector<int>& nums) {
        size_t n = nums.size() / 2;
        unordered_map<int, int> m;
        for (auto e : nums)
            m[e]++;

        for (auto& e : m)
            if (e.second == n)
                return e.first;
        return 0;
    }
};

8. 散列文件使用散列函数将记录的关键字值计算转化为记录的存放地址。由于散列函数不是一对一的关系，所以选择好的（）方法是散列文件的关键。 

A.散列函数
B.除余法中的质数
C.冲突处理
D.散列函数和冲突处理

答案：D
要使哈希高效：选择好的哈希函数非常关键，好的哈希函数可以减少发生冲突的概率，万一发生冲突，好的处理哈希冲突的方法也比较关键，否则冲突处理不当，也会增加后序元素冲突的概率

9. 散列函数有一个共同性质，即函数值应按（）取其值域的每一个值。 

A.最大概率
B.最小概率
C.同等概率
D.平均概率

答案：C
哈希函数设计原则：
1. 哈希函数应该尽可能简单
2. 哈希函数的值域必须在哈希表格的范围之内
3. 哈希函数的值域应该尽可能均匀分布，即取每个位置应该是等概率的

10. 下面关于哈希说法正确的是（）

A.哈希是一种查找的方法，不是数据结构
B.采用哈希方式解决问题时，可以不用哈希函数
C.哈希查找的时间复杂度一定是O(1)
D.哈希是以牺牲空间为代价，提高查询的效率

答案：D
A：错误，哈希是一种用来进行高效查找的数据结构，查找的时间复杂度平均为O(1)
B：错误，哈希之所以高效，是引用使用了哈希函数将元素与其存储位置之间建立了一一对应的关系，因此必须使用哈希函数
C：错误，不一定，因为存在哈希冲突，一般基本都是O(1)
D：正确，采用哈希处理时，一般所需空间都会比元素个数多，否则产生冲突的概率就比较大，影响哈希的性能

11. 下面关于哈希冲突说法正确的是（）

A.哈希冲突是可以通过设计好的哈希函数来杜绝的
B.哈希冲突是无法避免的
C.哈希冲突是不同的元素，通过不同的哈希函数而产生相同的哈希地址而引起的
D.哈希冲突产生的原因一定是插入了相同的元素

答案：B
A：错误，哈希冲突是不能杜绝的，这个与存储的元素以及哈希函数相关
B：正确
C：错误，哈希冲突是不同的元素，通过相同的哈希函数而产生相同的哈希地址而引起的，注意仔细看选项
D：错误，不同元素在计算出相同的哈希值时就会冲突

12. 将10个元素散列到100000个单元的哈希表中,则()产生冲突

A.一定会
B.一定不会
C.仍可能会
D.以上都不对

答案：C
只要想哈希表格中存储的元素超过两个，就有可能存在哈希冲突

13. 解决散列法中出现冲突问题常采用的方法是()

A.数字分析法、除余法、平方取中法
B.数字分析法、除余法、线性探测法
C.数字分析法、线性探测法、多重散列法
D.线性探测法、多重散列法、链地址法

答案：D
注意要区分清楚：哈希冲突的处理方法和哈希函数
哈希函数作用是：建立元素与其存储位置之前的对应关系的，在存储元素时，先通过哈希函数计算元素在哈希表格中的存储位置，然后存储元素。好的哈希函数可以减少冲突的概率，但是不能够绝对避免，万一发生哈希冲突，得需要借助哈希冲突处理方法来解决。
常见的哈希函数有：直接定址法、除留余数法、平方取中法、随机数法、数字分析法、叠加法等
常见哈希冲突处理：闭散列（线性探测、二次探测）、开散列(链地址法)、多次散列

14. 用哈希（散列）方法处理冲突（碰撞）时可能出现堆积（聚集）现象，下列选项中，会受堆积现象直接影响的是 ()

A.存储效率
B.数列函数
C.装填（装载）因子
D.平均查找长度

答案：D
冲突越多，查找时比较的次数就越多，对平均查找长度影响比较大。

15. 采用线性探测法处理散列时的冲突,当从哈希表删除一个记录时,不应将这个记录的所在位置置空,因为这会影响以后的查找() 

A.对
B.错
C.不一定
D.以上说法都不对

答案 ：A
线性探测采用未删除法，当从哈希表中删除某个元素时，并没有将该元素真正的删除掉，而是采用标记的方式处理，但是不能直接将该位置标记为空，否则会影响从该位置产生冲突的元素的查找。

16. 采用开放定址法处理散列表的冲突时，其平均查找长度？ 

A.高于链接法处理冲突
B.高于二分查找
C.低于链接法处理冲突
D.低于二分查找

答案：A
开放定址法一旦产生冲突，冲突容易连在一起，引起一连串的冲突，链地址法一般不会

17. 已知某个哈希表的n个关键字具有相同的哈希值，如果使用二次探测再散列法将这n个关键字存入哈希表，至少要进行（）次探测。

A.n-1
B.n
C.n+1
D.n(n+1)
E.n(n+1)/2
F.1+n(n+1)/2

答案：E
元素1：探测1次
元素2：探测2次
元素3：探测3次
.....
元素n：探测n次
故要将n个元素存入哈希表中，总共需要探测：1 + 2 + 3 + ... + n = n * (n + 1) / 2

18. 已知有一个关键字序列：（19,14,23,1,68,20,84,27,55,11,10,79）散列存储在一个哈希表中，若散列函数为H（key）=key%7，并采用链地址法来解决冲突，则在等概率情况下查找成功的平均查找长度为()

A.1.5
B.1.7
C.2.0
D.2.3

答案：A
[0] [1]   [2]   [3]   [4]   [5]   [6]
14  1    23   10   11   19   20
84        79                 68   27
                                        55

14、1、23、10、11、19、20: 比较1次就可以找到
84、79、68、27：需要比较两次才可以找到
55 : 需要比较三次才可以找到
总的比较次数为：7 + 4 * 2 + 3 = 18，总共有12个元素
故：等概率情况下查找成功的平均查找长度为：18 / 12 = 1.5

19. 现有容量为10GB的磁盘分区，磁盘空间以簇（cluster）为单位进行分配，簇的大小为4KB，若采用位图法管理该分区的空闲空间，即用一位（bit）标识一个簇是否被分配，则存放该位图所需簇的个数为 （）

A.80
B.320
C.80K
D.320K

答案：A
10GB = 10 * 1024 * 1024K  一个簇大小为4K，那10GB总共有 10 * 1024 * 1024 / 4 = 10 * 1024 * 256个簇
用位图来进行存储时：一个簇占用一个比特位，总共需要10 * 1024 * 256个比特位，
10 * 1024 * 256 bit = 10 * 1024 * 256 / 8字节 = 320K
一个簇大小为4K，故总共需要320K / 4k = 80个簇进行存储

20. 下面关于位图说法错误的是（）

A.位图就是用比特比特位表示一个数据的状态信息
B.通过位图可以求两个集合的交集
C.位图实际是哈希变形思想的一种应用
D.位图可以很方便的进行字符串的映射以及查找

答案：D
A：正确，位图概念
B：正确，将两个序列分别映射到两个位图上，对两个位图的每个字节进行按位与操作，结果为1的比特位对应的数据的就是两个序列的交集
C：正确，位图就是将数据与数据在位图中对应的比特位进行了一一对应，是哈希的一种变形
D：错误，采用位图标记字符串时，必须先将字符串转化为整形的数字，找到位图中对应的比特位，但是在字符串转整形的过程中，可能会出现不同字符串转化为同一个整形数字，即冲突，因此一般不会直接用位图处理字符串。

21. 下面关于布隆过滤器优缺点说法错误的是（）

A.布隆过滤器没有直接存储数据，可以对数据起到保护作用
B.布隆过滤器查找的结果不准确，并不能使用
C.布隆过滤器采用位图的思想表示数据装填，可以节省空间
D.布隆过滤器可能会存在误判，告知数据存在可能是不准确的

答案：B
A：正确，布隆过滤器底层使用的是位图，没有直接存储数据本身
B：错误，如果可以接受误差，是可以用的
C：正确
D：正确，因为多个元素的比特位上可能有重叠

22. 下面关于布隆过滤器说法不正确的是（）

A.布隆过滤器是一种高效的用来查找的数据结构
B.布隆过滤器弥补了位图不能存储字符串等类型得缺陷
C.可以使用布隆过滤器可以准确的告知数据是否存在
D.布隆过滤器不存储数据本身，是一种紧促的数据结构

答案：C
A：正确，因为其底层使用的是位图，而位图就是哈希的一种变形
B：正确，布隆过滤器可以映射存储任意类型，只是存在误判的问题
C：错误，布隆过滤器找到数据不存在，则该数据一定不存在，如果说存在，那可能存在，不存在一定是准确的，存在时可能会误判
D：正确，因为其底层使用位图，用比特位代表数据存在与否的状态信息，是一种紧促的数据结构

23. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法。如何扩展BloomFilter使得它支持删除元素的操作

精确结果：
注意该题不能直接使用位图。因为：假设将文件1中的每条query映射到位图中，然后检测第二个文件中的query是否在位图中出现过，在用query对位图进行操作时，必须将query转换为整形数字，而两个不同的query可能会转化为同一个记录，再到位图中进行查找时，可能就会认为这两条query是同一个，而将其当成交集，就会出错，结果就不精确。

采用哈希切割进行解决：
1. 将文件1进行哈希切割，将每条query按照切割结果放到对应的文件中
2. 对文件2中的query进行转化处理，看能落在哪个文件中，然后在该文件中检查该query是否出现过，如果出现过，则是交集，否则不是交集，对文件2中的每条query进行该种操作，最终就可以找到交集
缺陷：效率低

近似结果：
采用位图可以得到近似结果，不过误差可能大，因为一条记录对应一个比特位，冲突的概率比较多。采用布隆过滤器，用多个比特位表示一条query，可以降低出错的概率。

BloomFilter支持删除：
不使用比特位表示数据状态，可以将比特位扩展成整形变量，在插入数据时，该位置每被使用一次，就给该位置计数加1，删除数据时，给该位置数据减一即可，这样没删除一个数据，即使有位置重复，也不会对其他数据造成影响。
缺陷：可能存在计数回头，即计数溢出。

24. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

找文件的交集，相同的数据最后在结果中只需要出现一次即可，因此可以用位图直接解决：
1. 将两个文件中的数据分别映射到两个位图中，一个位图映射完的那个文件数据需要512M空间
计算方式：100亿个整形数据，有些数据肯定重复了，但是求交集不用管重复，给一个位图，位图中给2^32个比特位即可，2^32个比特位，2^32/8 = 2^29个字节/1024 = 2^19K个字节/1024 = 2^9M个字节=512M
2. 将两个位图对应的字节进行逻辑与
3. 统计位图中为1的比特位，该比特位对应的数字即为两个文件的交集，结束

25. 给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？ 与上题条件相同，如何找到top K的IP？如何直接用Linux系统命令实现？

log file太大，直接处理不好处理或者根本就不能一次性处理完，因此一般的处理方法都是对文件进行切割
1. 平均切割，不可取，因为平均切割实际和方法一类似
2. 采用哈希切割
a.确定文件被分割的次数，根据用户给的内存限制来确定切割份数，比如内存限制1G，至少要分割成100个小文件，甚至更多，分割文成后如果某个文件大小超过1G，增大份数，重新分割，直到每个文件大小小于1G
b.将IP地址转化为整形的数字(有专门的API函数可以转，学过网络就知道)，然后用该整形数字模文件份数，模完之后的结果就是该整形数字(即IP地址)所要放置的文件编号，对每个IP地址都进行该种操作，此操作称为哈希切割，与哈希桶的原理比较像，该种切割的好处是：相同的IP地址都在一个文件中，将来统计每个IP地址出现的次数时好统计，一个文件处理完，IP地址就的次数就统计出来了。
c.采用unordered_map统计每个文件中IP地址出现的次数
d.统计完成后找到出现次数最多的IP地址即可

找出现次数最多的前K个IP地址，经典的top - k问题，具体操作如下：
1. 使用哈希切割方式统计出每个IP地址出现的次数
2. 用<IP地址，出现次数>构建键值对，创建一个K个元素小堆，创建小堆时按照次数比较
3. 用剩余的IP地址次数依次与堆顶元素比较，如果次数：
小于等于堆顶IP地址出现次数，舍弃该IP地址
大于堆顶IP地址出现次数时，删除堆顶元素，将该IP地址以及其出现次数构建成键值对插入到堆中直到所有IP地址都操作完，最后堆中的K个IP地址就是出现次数最多的前K个IP地址