聚类算法

最新推荐文章于 2022-10-29 21:40:32 发布

原创最新推荐文章于 2022-10-29 21:40:32 发布 · 625 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#聚类 #算法 #机器学习 #python

本文深入探讨K-Means聚类算法及其优化方法Canopy算法，阐述了它们在用户画像和广告推荐等场景的应用，分析了算法的流程、优缺点，并介绍了特征降维技术如主成分分析(PCA)在算法优化中的作用。

应用场景:用户画像,广告推荐等等

一种典型的无监督学习算法,主要将相似的样本自动归到一个类别中,计算样本之间的相似性,一般使用欧式距离

聚类算法和分类算法的区别:

聚类算法时无监督的学习算法
分类算法属于监督的学习算法

流程:
1. 事先确定常数K,常数K意味着最终聚类类别数
2. 随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(欧氏距离),将样本点归到最相似的类中
3. 重新计算每个类的质心,重复这样的过程,直到质心不再改变
4. 最终就确定了每个样本所属的类别以及每个类的质心
5. 由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢
k-means算法小结

优点:

1.原理简单(靠近中心点),实现容易

2.聚类效果上(依赖K的选择)

3.空间复杂度o(N),时间复杂度o(IKN)

N为样本点个数，K为中心点个数，I为迭代次数

缺点:

1.对离群点,噪声敏感(中心点易偏移)

2.很难发现大小差别很大的簇及进行增量计算

3.结果不一定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
canopy算法配合初始类聚类实现流程

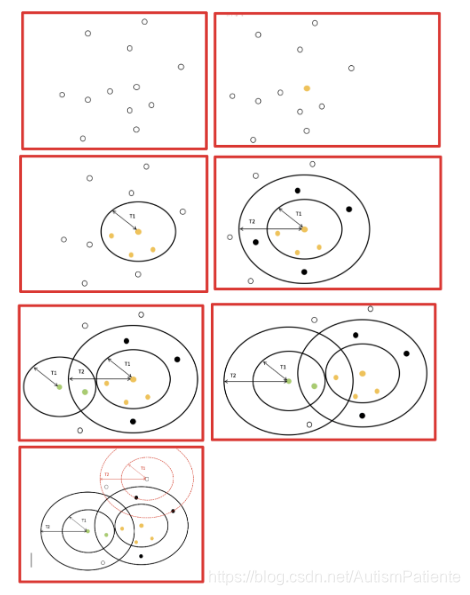
canopy算法的优缺点

优点:

1…Kmeans对噪声抗干扰较弱，通过Canopy对比，将较小的NumPoint的Cluster直接去掉有利于抗干扰

2.Canopy选择出来的每个Canopy的centerPoint作为K会更精确

3.只是针对每个Canopy的内做Kmeans聚类，减少相似计算的数量

缺点:

算法中 T1、T2的确定问题，依旧可能落入局部最优解

优化方法	思路
Canopy+kmeans	Canopy粗聚类配合kmeans
kmeans++	距离越远越容易成为新的质心
二分k-means	拆除SSE最大的簇
k-medoids	和kmeans选取中心点的方式不同
kernel kmeans	映射到高维空间
ISODATA	动态聚类，可以更改K值大小
Mini-batch K-Means	大数据集分批聚类

特征降维

指的是在某些限定条件下,降低随机变量(特征)个数,得到一组"不相关"主变量的过程(例如二维变成一位地球仪变成地图)
- 两种方式:
1.特征选择
```
  2.主成分分析(可以理解成特征提取)
```
- 特征选择:
  
  1.Filter(过滤式):主要探究特征本身特点,特征与特征和目标值之间的关联
  - 方差选择发:低方差特征过滤
    
    删除低方差的一些特征
    - 特征方差小:某个特征大多样本的值比较相近
    - 特征方差大:某个特征很多样本的值都有差别
  - 相关系数
    - 皮尔逊相关系数
      
      反映变量之间相关关系密切程度的统计指标
      
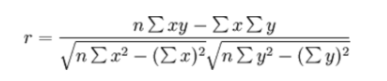
      相关系数的值介于–1与+1之间，即–1≤ r ≤+1。其性质如下：
      - 当r>0时，表示两变量正相关，r<0时，两变量为负相关
      - 当|r|=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系
      - 当0<|r|<1时，表示两变量存在一定程度的相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱
      - 一般可按三级划分：|r|<0.4为低度相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关
    - 斯皮尔曼相关系数
    - 反映变量之间相关关系密切程度的统计指标
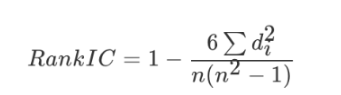
      - 斯皮尔曼相关系数表明 X (自变量) 和 Y (因变量)的相关方向。如果当X增加时， Y 趋向于增加, 斯皮尔曼相关系数则为正
      - 与之前的皮尔逊相关系数大小性质一样，取值 [-1, 1]之间
  2.Embedded(嵌入式):算法自动选择特征(特征与目标值之间的关联)
  - 决策树:信息熵,信息增益
  - 正则化:L1(把系数变为0) ,L2(把系数变成趋近于0的值)
  - 深度学习:卷积等
- 主成分分析(PCA)
  - 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量
  - 作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
  - 应用：回归分析或者聚类分析当中