【针对性复习】数据结构

于 2019-09-05 14:09:58 发布
阅读量499 收藏 1
点赞数 4
CC 4.0 BY-SA版权
分类专栏： 针对性复习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Austin_Yan/article/details/100537510

文章目录

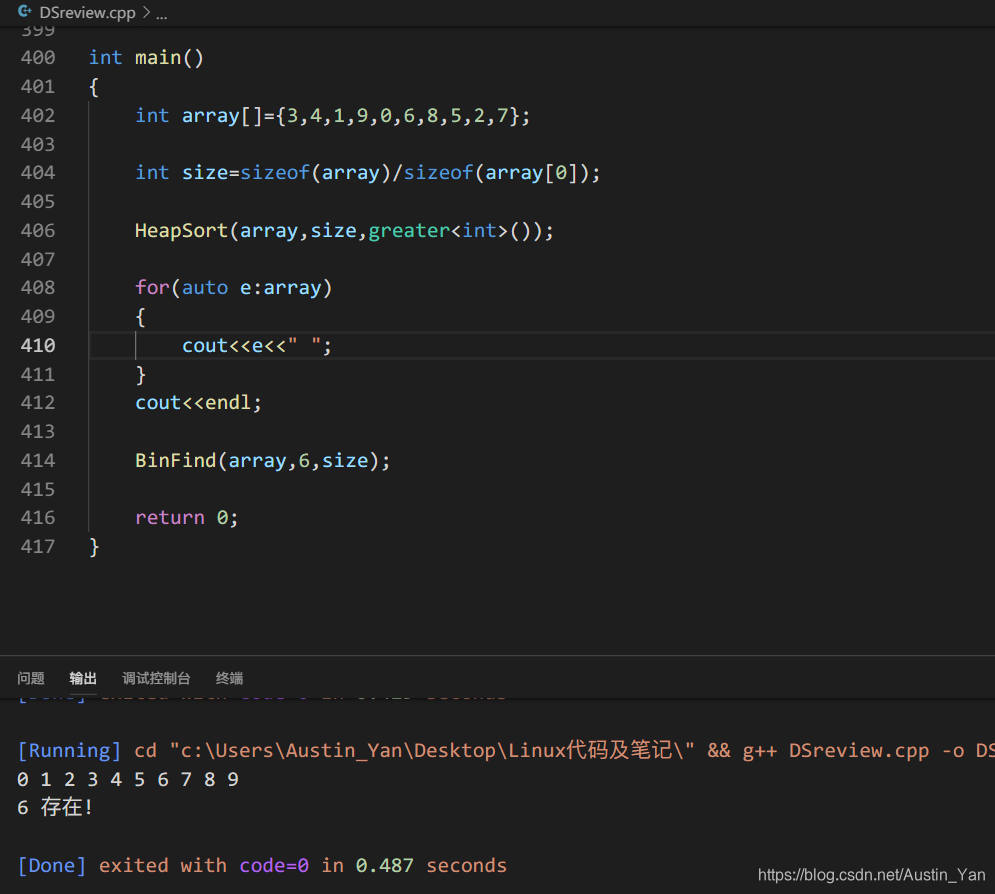
二分查找

bool BinFind(int* array, int data, int size)
{
	int left = 0;
	int right = size - 1;

	while (left <= right)
	{
		int mid = (left + right) >> 1;

		if (data<array[mid])
		{
			right = mid - 1;
		}
		else if (data>array[mid])
		{
			left = mid + 1;
		}
		else
		{
			cout << data << " 存在!" << endl;
			return true;
		}
	}

	cout << data << " 不存在!" << endl;
	return false;
}

在这里插入图片描述

链表面试题

前面已经写过博客了,这次是复习,多敲代码总没坏处

在带头节点的链表中头结点存放节点个数不合理，char的表示范围不够-128~127

面试题不特殊说明，就是不带头结点的单链表

不需要给出节点的定义

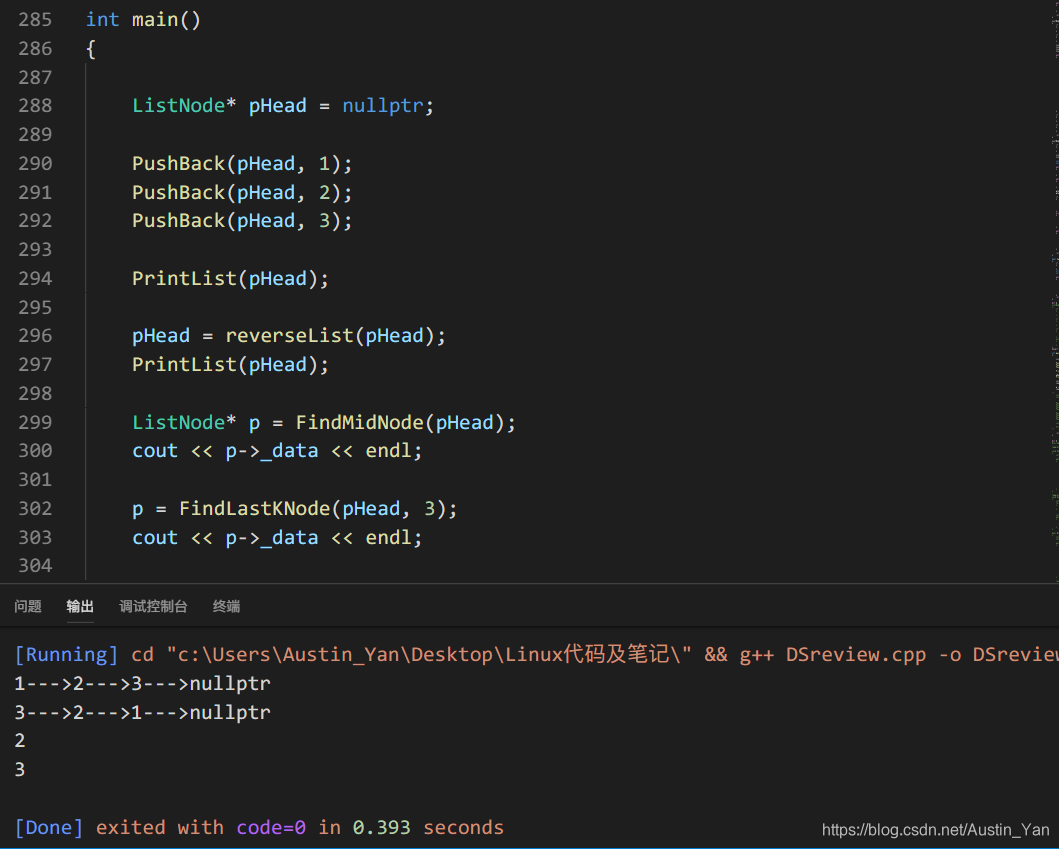
//写一个尾插

void PushBack(ListNode*& pHead, int data)
{
	if (pHead == nullptr)
	{
		pHead = new ListNode(data);
	}

	else
	{
		ListNode* pCur = pHead;

		while (pCur->pNext != nullptr)
		{
			pCur = pCur->pNext;
		}

		pCur->pNext = new ListNode(data);
	}
}

//写一个链表(不带环)逆置

ListNode* reverseList(ListNode* pHead)
{
	ListNode* result = nullptr;
	ListNode* pCur = pHead;

	while (pCur != nullptr)
	{
		ListNode* next = pCur->pNext;

		pCur->pNext = result;
		result = pCur;
		pCur = next;
	}
	return result;
}

//找链表的中间节点

ListNode* FindMidNode(ListNode* pHead)
{
	if (pHead == nullptr)
	{
		return nullptr;
	}

	ListNode* pFast = pHead;
	ListNode* pSlow = pHead;

	while (pFast!= nullptr && pFast->pNext != nullptr)
	{
		pFast = pFast->pNext->pNext;
		pSlow = pSlow->pNext;
	}

	return pSlow;
}

//找倒数第K个节点

ListNode* FindLastKNode(ListNode* pHead,size_t k)
{
	if (pHead == nullptr)
	{
		return nullptr;
	}

	ListNode* pFast = pHead;
	ListNode* pSlow = pHead;

	while (k--)
	{
		//K大于链表长度
		if (pFast == nullptr)
		{
			return nullptr;
		}

		pFast = pFast->pNext;
	}

	while (pFast != nullptr && pFast->pNext != nullptr)
	{
		pFast = pFast->pNext->pNext;
		pSlow = pSlow->pNext;
	}

	return pSlow;
}

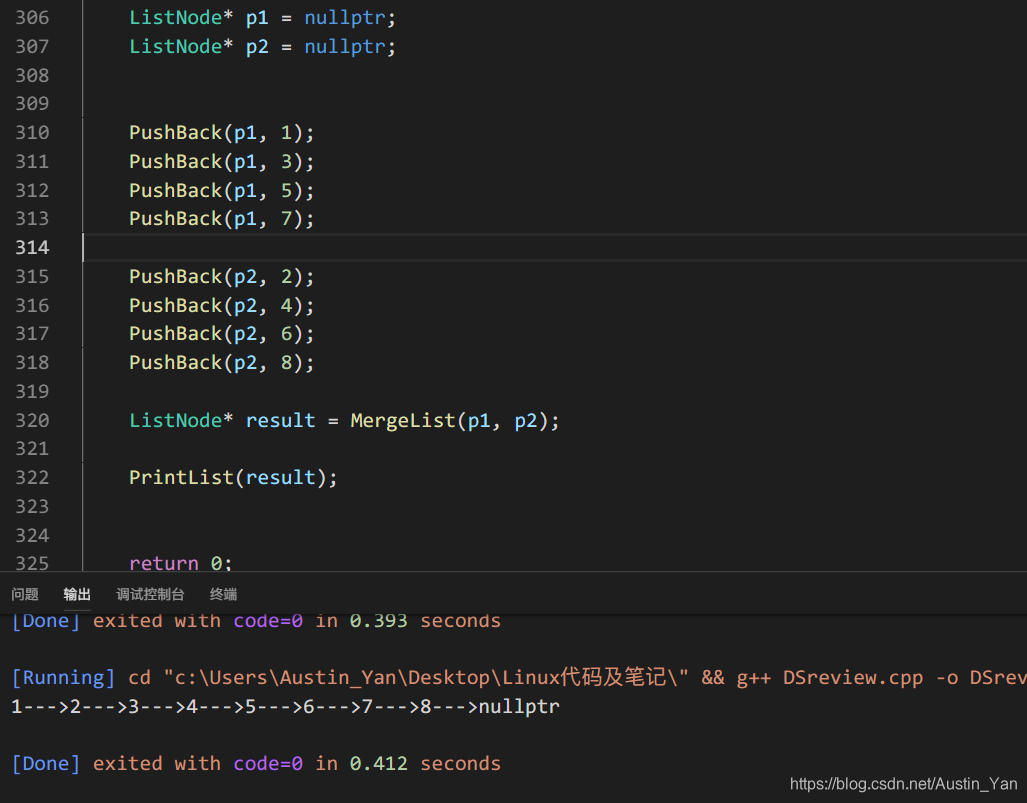
在这里插入图片描述

//合并两个有序链表

ListNode* MergeList(ListNode* pHead1, ListNode* pHead2)
{
	if (pHead1 == nullptr)
	{
		return pHead2;
	}

	if (pHead2 == nullptr)
	{
		return pHead1;
	}

	ListNode* result = nullptr;
	ListNode* last = nullptr;
	ListNode* pCur1 = pHead1;
	ListNode* pCur2 = pHead2;

	while (pCur1 != nullptr && pCur2 != nullptr)
	{
		if (pCur1->_data < pCur2->_data)
		{
			if (result == nullptr)
			{
				result = last = pCur1;
			}
			else
			{
				last->pNext = pCur1;
				last = pCur1;
			}
			pCur1 = pCur1->pNext;
		}
		else
		{
			if (result == nullptr)
			{
				result = last = pCur2;
			}
			else
			{
				last->pNext = pCur2;
				last = pCur2;
			}
			pCur2 = pCur2->pNext;
		}
	}

	if (pCur1 != nullptr)
	{
		last->pNext = pCur1;
	}

	if (pCur2 != nullptr)
	{
		last->pNext = pCur2;
	}

	return result;
}

在这里插入图片描述

//找两个链表相交的节点(不带环)

    ListNode* getIntersectionNode(ListNode* pHead1, ListNode* pHead2)
    {
        if (pHead1 == nullptr || pHead2 == nullptr)
        {
            return nullptr;
        }

        ListNode* pCur1 = pHead1;
        ListNode* pCur2 = pHead2;

        size_t size1 = 1;
        size_t size2 = 1;

        while (pCur1 != nullptr)
        {
            size1++;
            pCur1 = pCur1->next;
        }

        while (pCur2 != nullptr)
        {
            size2++;
            pCur2 = pCur2->next;
        }

        pCur1 = pHead1;
        pCur2 = pHead2;
        
        if (size1 > size2)
        {
            while (size1 > size2)
            {
                pCur1 = pCur1->next;
                size1--;
            }
        }
        else
        {
            while (size2 > size1)
            {
                pCur2 = pCur2->next;
                size2--;
            }
        }

        while (pCur1 != nullptr && pCur2 != nullptr)
        {
            if (pCur1 == pCur2)
            {
                return pCur1;
            }

            pCur1 = pCur1->next;
            pCur2 = pCur2->next;
        }

        return nullptr;
    }

慢指针:L+X
快指针:L+X+nr

2*(L+X)=L+X+nr

L=nr-X,n=1,2,3…

复杂链表的复制

  • 在每个节点后面插入值相同的新节点
  • 给新节点的随机指针域赋值
    • p2放在p1的next,p2指向p1随机指针域的next
    • p1放在p2的next,p2放在p1的next
  • 把新链表拆分出去
    • p1->next指向p2->next
    • p1放在p2,p2指向p1->next

顺序表和链表的区别

  • 空间:
    • 一段连续的空间
      • 插入可能需要扩容
    • 底层空间不连续(逻辑顺序通过指针连接顺序)
      • 不需要扩容(New节点)
  • 效率:
    • 插入和删除效率低(需要搬移元素,O(N))
    • 插入和删除效率高(O(1))
  • 空间利用率:
    • 一整块空间
    • 小的节点
      • 内存碎片,效率低,额外空间浪费(保存的有结构体)
  • 应用场景:
    • 插入和删除操作不多
    • 插入和删除操作频繁
  • 缓存利用率:
    • 利用率高
    • 利用率低

vector和list的区别

  • 底层结构
    • 动态顺序表,一段连续的空间
    • 带头结点的双向循环链表
  • 随机访问能力
    • 支持,访问某个元素O(1)
    • 不支持,访问某个元素O(N)
  • 插入和删除
    • 插入和删除需要搬移元素,时间复杂度O(N),可能还需要增容,开辟新空间,拷贝元素,释放旧空间
    • 插入和删除方便,时间复杂度O(1)
  • 空间利用率
    • 底层是连续的空间,不容易造成内存碎片,空间利用率高,缓存利用率高
    • 底层节点动态开辟,容易造成内存碎片,空间利用率低,缓存利用率低
  • 迭代器
    • 原生态指针
    • 对原生态指针的封装
  • 迭代器失效
    • 插入时,要给所有的迭代器重新赋值(因为插入有可能会导致扩容),删除时,当前迭代器失效,需要重新赋值
    • 插入时,不会导致迭代器失效,删除时,只会导致当前迭代器失效,其他迭代器不受影响
  • 应用场景
    • 需要高效存储,支持随机访问,不关心插入删除效率低
    • 大量插入和删除操作,不关心随机访问

环形队列队满和队空

  • 空链表:
    • front==rear
  • 标记
    • flag == 0 && rear==front,队列空
    • flag == 1 && rear==front,队列满
  • 少存一个元素
    • (rear+1)%capacity==front,可能会越界
  • 取模
    • rear%=capacity,效率不高
    • if(rear==capacity){rear=0;}
//队列模拟实现栈

//最好按照模板来写

template <typename T>

class StackByQueue
{
public:
	void push(const T& data)
	{
		if (q1.empty() == true)
		{
			q2.push(data);
		}
		else
		{
			q1.push(data);
		}
	}

	void pop()
	{
		while (q1.size() > 1)
		{
			q2.push(q1.front());
			q1.pop();
		}
		q1.pop();
	}

	T& top()
	{
		if (q1.empty() == true)
		{
			return q2.back();
		}
		else
		{
			return q1.back();
		}
	}

	bool empty()
	{
		if (q1.empty() == true && q2.empty() == true)
		{
			return true;
		}
		return false;
	}

private:
	queue<T> q1;
	queue<T> q2;
};

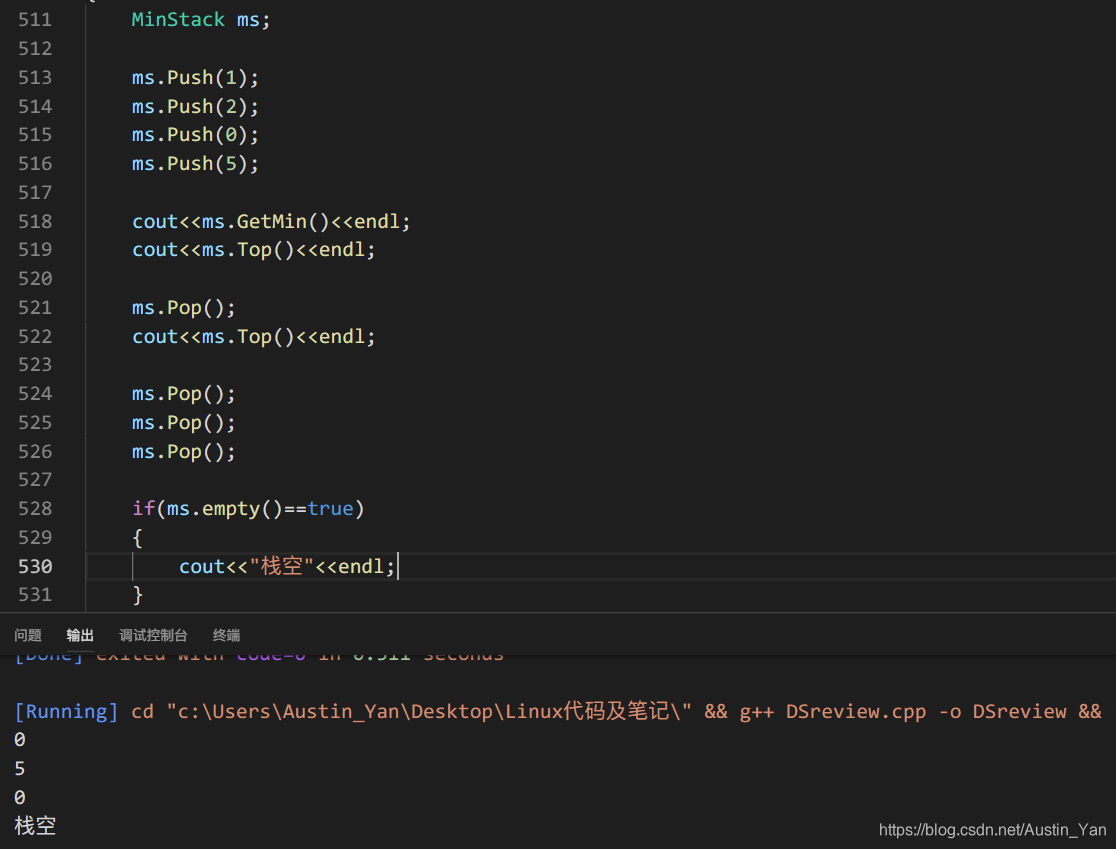
//写一个最小栈

//1.使用两个栈
//2.一次存两个值,一个正常插入的一个最小值
#include<stack>

class MinStack
{
public:
	MinStack()
	{}
	
	//使用方法二，一次存入两个元素
	void Push(int data)
	{
		//插入数据到s中
		if(s.empty()==true)
		{
			s.push(data);
			s.push(data);
		}
		else
		{
			int a=s.top();
			s.pop();

			int Min=s.top();

			if(data<=Min)
			{
				s.push(a);

				s.push(data);
				s.push(data);
			}
			else
			{
				s.push(a);

				s.push(Min);
				s.push(data);
			}
			
		}
	}

	void Pop()
	{
		s.pop();
		s.pop();
	}

	int Top()
	{
		return s.top();
	}

	int GetMin()
	{
		int a=s.top();
		s.pop();

		int Min=s.top();
		s.push(a);

		return Min;
	}

	bool empty()
	{
		if(s.empty()==true)
		{
			return true;
		}
		return false;
	}

private:
	stack<int> s;
};

在这里插入图片描述

//逆波兰表达式(Reverse Polish Notation)

//(1+2)*(3+4)--->12+34+*

二叉树

  • 树相关的概念:

    • 双亲:若一个节点含有子节点,则这个节点是这个子节点的双亲节点
    • 高度:树中节点的最大层次
    • 兄弟:有相同双亲节点的被称为兄弟节点
    • 节点的度:结点子树的个数
    • 叶子节点:度为0的节点被称为叶节点

  • 表示方式:

    • 孩子表示法
    • 双亲表示法
    • 孩子双亲表示法
    • 孩子兄弟表示法

  • 二叉树概念:

    • 空树，根+根的左子树+根的右子树

  • 特殊二叉树:

    • 满二叉树:每一层节点都达到了最大值
    • 完全二叉树:前N个节点与满二叉树的前N个节点分布形式完全相同

  • 二叉树的五条性质:

    • 1.若规定根节点的层次为1,则一颗非空二叉树的第i层最多有2^(i-1)个节点

    • 2.若规定只有根节点的二叉树深度为1,则深度为k的二叉树最大节点数是2^k-1

    • 3.对任意一颗二叉树,如果其叶节点个数为n0,度为2的非叶节点个数为n2,则有n0=n2+1

    • 4.具有n个节点的完全二叉树的深度k为log2(n+1)向上取整

    • 5.对于有n个节点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0进行编号

      • 则对于序号为i的节点有:

        • <1>.若i>0,双亲序号:(i-1)/2i=0,i为根节点编号,无双亲节点

        • <2>.若2i+1<n,左孩子序号:2i+1,否则无左孩子

        • <3>.若2i+2<n,右孩子序号:2i+2,否则无右孩子

一个完全二叉树1000个节点,____个叶子节点,____个非叶子节点,____个只有左孩子,____个只有右孩子

假设二叉树总共有N个节点,n0,n1,n2,N=n0+n1+n2

完全二叉树—>n0+1+n2=1000—>2*n2=998—>n2=499—>n0=500

1个只有左孩子,0个只有右孩子

二叉树的存储

https://blog.youkuaiyun.com/Austin_Yan/article/details/97931649

  • 顺序结构

    • 堆,只适合完全二叉树,否则空间会大量浪费
    • 向下调整
      • 看是否调整到最后一个节点,while (child < size)
      • 优先找到左孩子
      • 左右孩子中较小的(右孩子必须存在),用child标记
      • 双亲与孩子交换,swap(C++标准库提供)
      • parent放在child位置,child重新计算
      • 如果随机数组一开始就不满足堆的性质,先找到倒数第一个非叶子节点
      • lastleaf = (size - 2) >> 1;
      • 在处理上一个叶子节点,直到全处理完
    • 向上调整(插入)
      • 通过孩子找双亲,parent=(child-1)>>1
      • 孩子如果比双亲小,交换位置swap(C++标准库提供)
      • child放在parent位置,parent重新计算
      • 看是否调整到第一个节点,while (child != 0)
    • 堆的删除
      • 把堆顶元素和最后一个元素互换
      • 更新元素个数,size–;
      • 使用向下调整
    • 堆排
      • 创建堆(向下调整),从倒数第一个叶子节点
      • 首末元素交换,size–
      • 重复过程

  • 链式结构

    • 获取树的高度
      • 空树,返回0
      • 只有根节点,返回1
      • 返回根的左子树的高度+根的右子树高度
    • 获取叶子节点的个数
      • 空树,返回0
      • 只有根节点,返回1
      • 返回根的左子树叶子节点个数+根的右子树叶子节点个数
    • 获取K层的节点数
      • 如果空树,或者K=0,返回0
      • 如果只有K=1,只有根节点,返回1
      • 返回K-1的左子树作为根节点的节点个数+K-1的右子树作为根节点的节点个数
    • 获取节点的双亲
      • 树不存在,或者节点为根节点,返回nullptr
      • 节点若是根节点左孩子或者右孩子,返回根节点
      • 去根的左子树中查找,存在就返回,否则去根的右子树中查找
//写一个堆排(向下调整)
template<typename T,typename Compare>

void HeapAdjust(T* array, int size, int parent,Compare com)
{
	int child = parent * 2 + 1;

	while (child < size)
	{
		if (child + 1 < size && com(array[child + 1] , array[child]))
			child += 1;

		if (com(array[child] , array[parent]))
		{
			swap(array[child], array[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}

template<typename T,typename Compare>

void HeapSort(T* array, int size,Copmare com)
{
	int root = ((size - 1 - 1) >> 1);
	for (root; root >= 0; --root)
	{
		HeapAdjust(array, size, root,com);
	}


	int end = size - 1;
	while (end != 0)
	{
		swap(array[0], array[end]);
		HeapAdjust(array, end, 0);
		end--;
	}
}

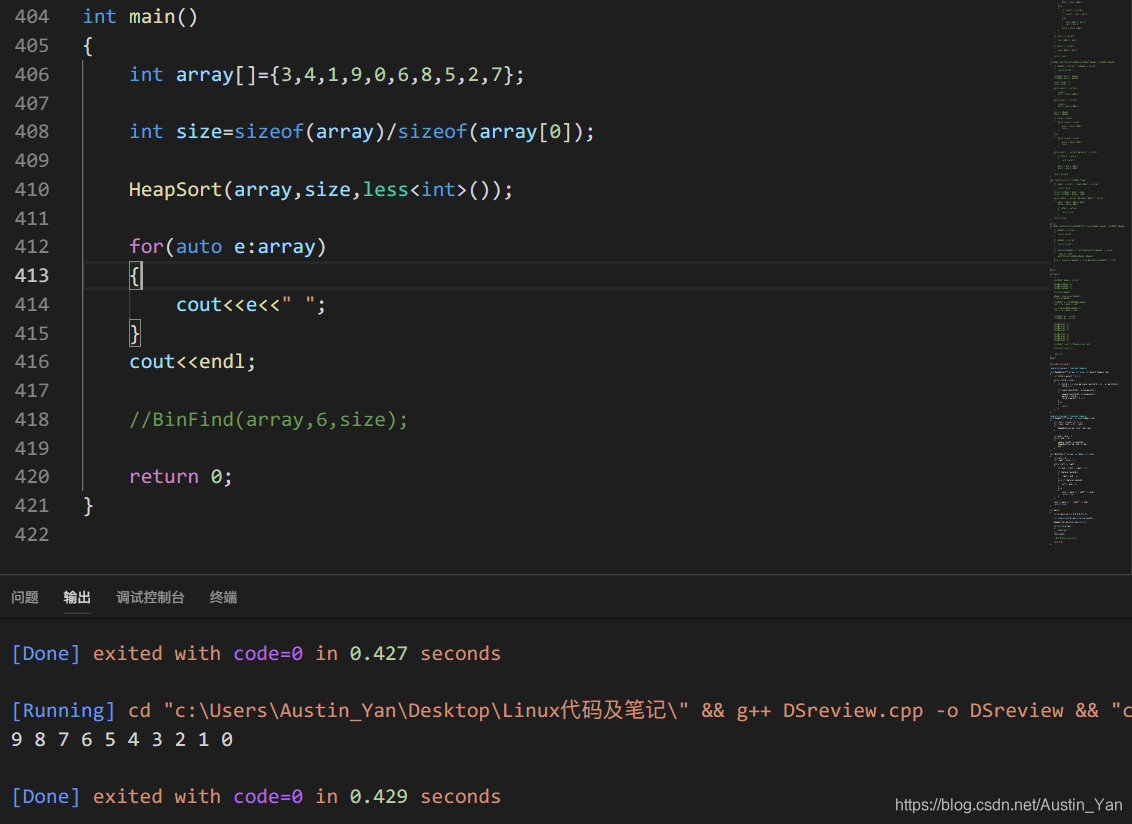
在这里插入图片描述

二叉树的创建

#include<vector>

struct BTNode
{
	BTNode(int data):_data(data),_pLeft(nullptr),_pRight(nullptr)
	{

	}

	BTNode* _pLeft;
	BTNode* _pRight;
	int _data;
};

BTNode* CreateBinTree(vector<int> v,int& index,int mark)
{
	if(index>=v.size() || v[index]==mark)
	{
		return nullptr;
	}

	BTNode* pRoot=new BTNode(v[index]);

	index++;
	pRoot->_pLeft=CreateBinTree(v,index,mark);

	index++;
	pRoot->_pRight=CreateBinTree(v,index,mark);

	return pRoot;
}

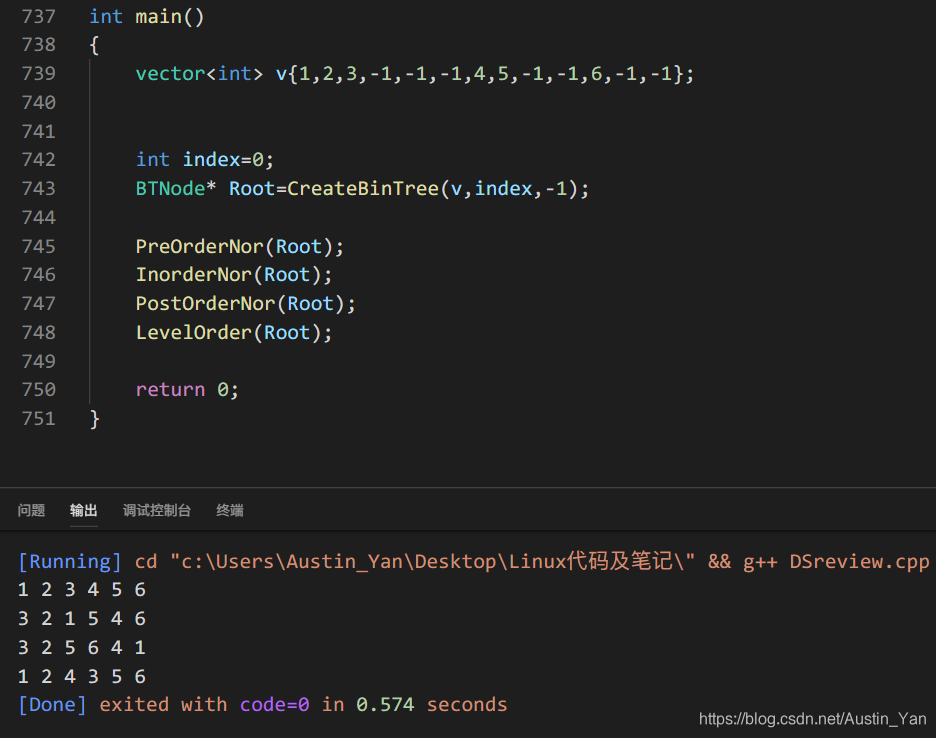
非递归前、中、后序遍历

  • 前序遍历
    • 检测栈是否为空
    • 获取栈顶元素,遍历
    • 如果有左右子树,压栈先放入右子树,在放入左子树
  • 中序遍历
    • 找到根节点最左侧的待遍历节点
    • 保存路径上所有节点
    • 获取栈顶元素,遍历,pop出栈
    • 把最左侧节点的右子树当成一棵单独的树处理
  • 后序遍历
    • 找到根节点最左侧的待遍历节点
    • 保存路径上所有节点
    • 获取栈顶元素,最左侧节点,如果其没有右孩子,或者右孩子被遍历过(判断ptop->right==prev),遍历此节点
    • 如果有右孩子,pcur=ptop->right,循环继续
#include<stack>

void PreOrderNor(BTNode* pRoot)
{
	if(pRoot==nullptr)
	{
		return;
	}

	stack<BTNode*> s;
	s.push(pRoot);

	while(s.empty()!=true)
	{
		BTNode* pCur=s.top();
		cout<<pCur->_data<<" ";

		s.pop();

		if(pCur->_pRight!=nullptr)
		{
			s.push(pCur->_pRight);
		}

		if(pCur->_pLeft!=nullptr)
		{
			s.push(pCur->_pLeft);
		}
	}
	cout<<endl;
}

void InorderNor(BTNode* pRoot)
{
	if(pRoot==nullptr)
	{
		return;
	}

	stack<BTNode*> s;
	BTNode* pCur=pRoot;

	while(s.empty()!=true || pCur!=nullptr)
	{
		while(pCur!=nullptr)
		{
			s.push(pCur);
			pCur=pCur->_pLeft;
		}

		pCur=s.top();
		cout<<pCur->_data<<" ";

		s.pop();
		pCur=pCur->_pRight;
	}
	cout<<endl;
}

void PostOrderNor(BTNode* pRoot)
{
	if(pRoot==nullptr)
	{
		return;
	}

	stack<BTNode*> s;
	BTNode* pCur=pRoot;
	BTNode* pPrev=nullptr;

	while(s.empty()!=true || pCur!=nullptr)
	{
		while(pCur!=nullptr)
		{
			s.push(pCur);
			pCur=pCur->_pLeft;
		}

		BTNode* pTop=s.top();

		if(pTop->_pRight==nullptr || pTop->_pRight==pPrev)
		{
			cout<<pTop->_data<<" ";
			pPrev=pTop;
			s.pop();
		}
		else
		{
			pCur=pTop->_pRight;
		}
	}
	cout<<endl;
}

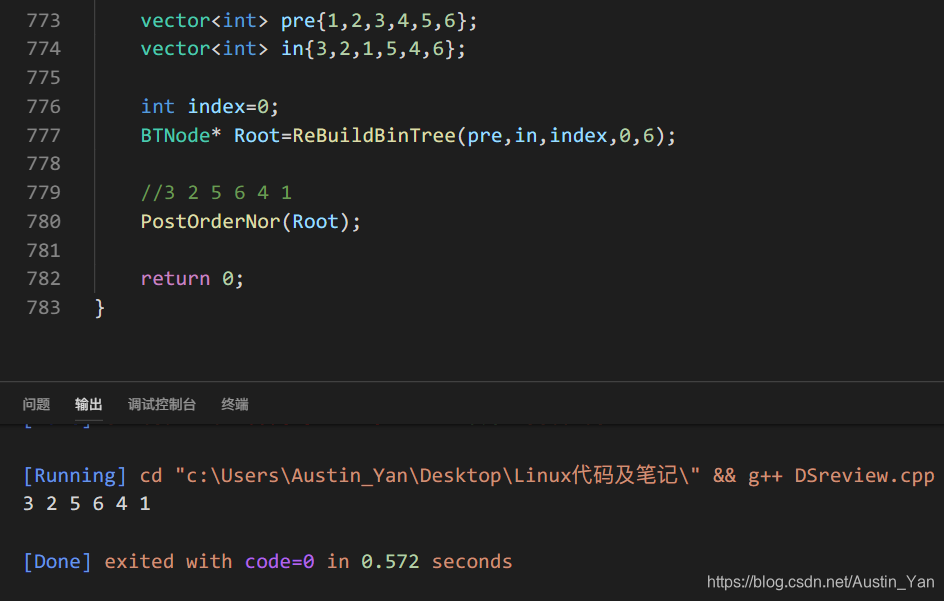
在这里插入图片描述

重建二叉树

  • 从前序遍历结果拿到根节点
  • 从中序遍历结果确认根的左右子树
  • 建立区间,[left,Inindex),[Inindex+1,right)
  • 前段区间递归建立左子树,后段区间递归建立右子树
  • 递归前注意++index,根节点创建完之后索引朝后走
  • 注意Inindex防止越界,if(left<Inindex),if(Inindex+1<right)
BTNode* ReBuildBinTree(const vector<int>& pre, const vector<int>& in, int& index, int left, int right)
{
	if (left >= right)
	{
		return nullptr;
	}

	BTNode* pRoot = new BTNode(pre[index]);

	int Inindex = 0;
	while (in[Inindex] != pre[index])
	{
		Inindex++;
	}

	if (left < Inindex)
	{
		pRoot->_pLeft = ReBuildBinTree(pre, in, ++index, left, Inindex);
	}

	if (Inindex + 1 < right)
	{
		pRoot->_pRight = ReBuildBinTree(pre, in, ++index, Inindex + 1, right);
	}

	return pRoot;
}

在这里插入图片描述

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值