【LeetCode】LCR 121. 寻找目标值 - 二维数组

AustinCyy

于 2025-02-17 14:40:08 发布

阅读量1k

点赞数 25

CC 4.0 BY-SA版权

分类专栏： leetcode题解文章标签： leetcode 算法职场和发展

本文链接：https://blog.youkuaiyun.com/AustinCyy/article/details/145669374

leetcode题解专栏收录该内容

6 篇文章

订阅专栏

题目

LCR 121. 寻找目标值 - 二维数组 - 中等 - 数组

m*n 的二维数组 plants 记录了园林景观的植物排布情况，具有以下特性：

每行中，每棵植物的右侧相邻植物不矮于该植物；
每列中，每棵植物的下侧相邻植物不矮于该植物。

请判断 plants 中是否存在目标高度值 target。

示例 1：

输入：plants = [[2,3,6,8],[4,5,8,9],[5,9,10,12]], target = 8

输出：true

示例 2：

输入：plants = [[1,3,5],[2,5,7]], target = 4

输出：false

提示：

0 <= n <= 1000
0 <= m <= 1000

题解

这个方法来自 Krahets，太强了。

分治法的基本思想： 将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治策略： 对于一个规模为n的问题，若该问题可以容易的解决(比如规模n较小)则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解决这些子问题，然后将各个子问题的解合并得到原问题的解。

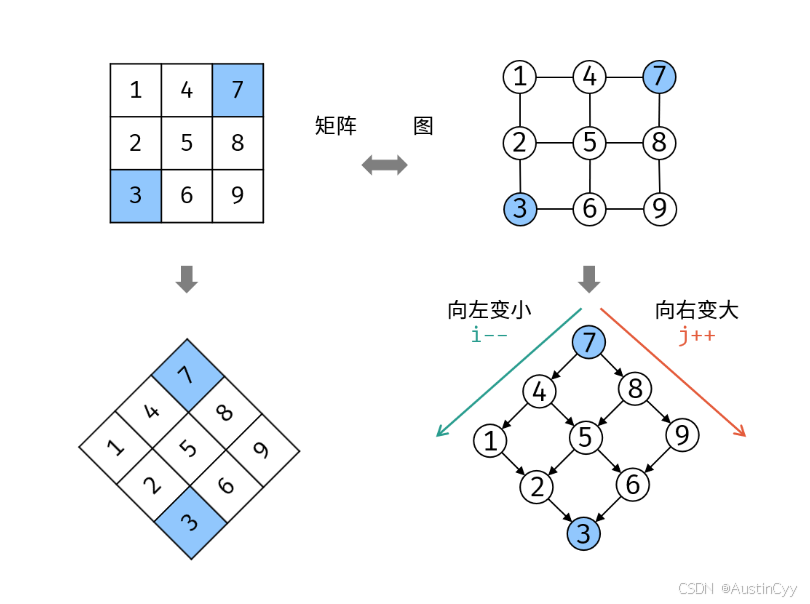
如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于二叉搜索树，即对于每个元素，其左分支元素更小、右分支元素更大。

因此，考虑从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

在这里插入图片描述

算法流程：
“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素。以 plants 中的左下角元素为起始点，则有:

从矩阵 plants 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：

当 plants[i][j] > target 时，执行 i-- ，即消去第 i 行元素；
当 plants[i][j] < target 时，执行 j++ ，即消去第 j 列元素；
当 plants[i][j] = target 时，返回 true ，代表找到目标值。

若行索引或列索引越界，则代表矩阵中无目标值，返回 false 。

每轮 i 或 j 移动后，相当于生成了“消去一行（列）的新矩阵”，索引(i,j) 指向新矩阵的左下角元素，因此可重复使用以上性质消去行（列）。

class Solution(object):
    def findTargetIn2DPlants(self, plants, target):
        """
        :type plants: List[List[int]]
        :type target: int
        :rtype: bool
        """
        i, j = len(plants) - 1, 0
        while i >= 0 and j < len(plants[0]):
            if plants[i][j] > target: i -= 1
            elif plants[i][j] < target: j += 1
            else: return True
        
        return False