归一化
前言:上次的GoogLeNet里的V2版本的伟大贡献是提出了Batch Normalization(BN),于是就准备了解一下BN,顺便学一下其他不同的归一化方式。
背景
深层神经网络中,中间某一层的输入是其之前的神经层的输出。因此,其之前的神经层的参数变化会导致其输入的分布发生较大的差异。利用随机梯度下降更新参数时,每次参数更新都会导致网络中间每一层的输入的分布发生改变。越深的层,其输入分布会改变的越明显。
内部协变量偏移(Internal Covariate Shift):每一层的参数在更新过程中,会改变下一层输入的分布,神经网络层数越多,表现得越明显,(就比如高层大厦底部发生了微小偏移,楼层越高,偏移越严重。)
为了解决内部协变量偏移问题,就要使得每一个神经层的输入的分布在训练过程要保持一致。
归一化的作用:
- 提高精度
- 加快训练速度
- 防止梯度消失
四种归一化的区别

上图为四种归一化方法,其中N为批量,C为通道,(H,W)表示feature map,蓝色部分则代表输入集合。
[4,3,240,240]代表输入有四张图片,有个图片有三个通道,大小是240$\times$240
BN(Batch Normalization)是分三次进行归一化,每次对四张图片的某一个通道进行归一化
LN(Layer Normalization)是分四次进行归一化,每次对一整张图片的所有通道进行归一化
IN(Instance Normalization)是分 3 × 4 3\times4 3×4次进行归一化,每一张图片的每一个通道分别做归一化
GN(Group Normalization)是 在IN基础上分个组,即第二个参数如果是3,那么每一次就一张图片的三个通道做归一化
BN
均值的计算,就是在一个批次内,将每个通道中的数字单独加起来,再除以N × \times × H × \times ×W 。举个例子:该批次内有10张图片,每张图片有三个通道RBG,每张图片的高、宽是H、W,那么均值就是计算10张图片R通道的像素数值总和除以10 × \times × H × \times × W ,再计算B通道全部像素值总和除以10 × \times × H × \times ×W,最后计算G通道的像素值总和除以10 × \times × H × \times × W。方差的计算类似。
可训练参数 γ \gamma γ、 β \beta β 的维度等于张量的通道数,在上述例子中,RBG三个通道分别需要一个 γ \gamma γ 和一个 β \beta β ,所以 γ → \overrightarrow{\gamma} γ、 β → \overrightarrow{\beta} β 的维度等于3。
核心公式:
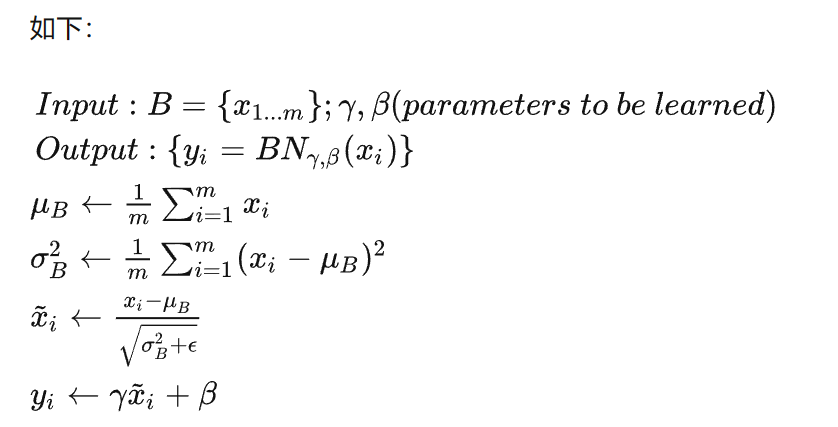
γ \gamma γ、 β \beta β 是可训练参数,参与整个网络的BP;
步骤:先计算 B 的均值和方差,之后将 B 集合的均值、方差变换为0、1( x i ← x i − u b σ b 2 + ϵ x_i \leftarrow \frac{x_i-u_b}{\sqrt{\sigma_b^2+\epsilon}} xi←σb2+ϵxi−ub)
最后将B中每个元素乘以 γ \gamma γ 再加 β \beta β ,输出。





 文章介绍了归一化在深度学习中的重要性,特别是针对内部协变量偏移问题。BatchNormalization(BN)、LayerNormalization(LN)、InstanceNormalization(IN)和GroupNormalization(GN)是四种主要的归一化方法。BN对每个批次的通道进行归一化,LN对每个图片的所有通道归一化,IN则对每个图片的每个通道独立归一化,而GN是对通道进行分组归一化。这些技术有助于提高模型精度,加速训练并缓解梯度消失问题。
文章介绍了归一化在深度学习中的重要性,特别是针对内部协变量偏移问题。BatchNormalization(BN)、LayerNormalization(LN)、InstanceNormalization(IN)和GroupNormalization(GN)是四种主要的归一化方法。BN对每个批次的通道进行归一化,LN对每个图片的所有通道归一化,IN则对每个图片的每个通道独立归一化,而GN是对通道进行分组归一化。这些技术有助于提高模型精度,加速训练并缓解梯度消失问题。
















 3460
3460

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








