强化学习基本概念

WanGxxxx.

已于 2025-03-02 15:46:25 修改

阅读量526

点赞数 8

分类专栏：强化学习文章标签： servlet 深度学习人工智能

于 2024-12-17 19:41:16 首次发布

本文链接：https://blog.youkuaiyun.com/ArtoriaLili/article/details/144531331

版权

强化学习专栏收录该内容

6 篇文章

订阅专栏

b站视频课程：第1课-基本概念（State,action,policy等）_哔哩哔哩_bilibili

第一节课被广泛使用的一个例子 grid-wrold example,一个网格世界，机器人在其中运动。网格的类型不同，有accessible可进入，forbidden禁止，target目标，三个网格，目的就是在最短的步骤从出发点经过accessible网格进入目标区域。这个网格世界是有个边界的，机器人在相邻块移动，不能斜着移动。

一、State

这是这节课的一个重要概念，相对于环境的一个状态 status，在这个网格世界中，指的就是location-位置，在上面的网格中，有 $s_1,s_2,\ldots,s_9$ ,多个location，那么我们就用这些字母表示这些状态，这个s可以理解为一个向量，存储x，y坐标，如果是更复杂的问题，那还有其他位置、速度信息。我们把这些数据放到一起 $\mathcal{S}=\{s_i\}_{i=1}^9$ ，就得到了现代控制理论中说的状态空间。

这个空间就是一个集合 set，就像之前LQR里面位置速度的集合。

二、Action

基本概念action，就相当于我在每一个状态实际上都是有一系列的可采取行动

在这里面就是有五种行动，a1 - a5 分别对应上下左右原地，我们也把这些所有的action放到一起，就得到了 Action space of a state

${\mathcal{A}(s_i)=\{a_i\}_{i=1}^5}$ Action space和 state是依赖的，不同的状态对应的运动策略自然是不同的。

三、 State transiton

当我们采取一个行动，那这个 agent 可以从一个 state 移动到另一个 state，这就是这样的一个过程。 $s_1\xrightarrow{a_2}s_2$ 以这个为例子，如果我在s1,那么采取行动a2后，就会到s2这个状态，这样一个过程就可以用这个式子来表示。这个概念实际上是定义 action和环境的一种交互行为。但是这个与环境的状态交互，在仿真中由我们定义，实际中起始是根据物理模型分析的。

上面我们说到的 Forbidden区，这块位置是可以进去的，但是进去了会被惩罚，如果物理上无法进入，那么就要在transiton定义状态，但是现在我们定义的是第一种状态。这种状态变化，我们也可以用一个表格来表示。

表格每一行对应一个状态，每一列对应一个action。但是如果存在多种可能性，那么表格肯定无法表达，那么一般的方法就是 State transition probability,引入了概率，那么这个就是条件概率。

$\begin{aligned}p(s_2|s_1,a_2)&=1\\p(s_i|s_1,a_2)&=0\quad\forall i\neq2\end{aligned}$

直管来说，当前位置在s1,采取a2的行动，下一时刻跳动s2的概率是多少

四、Policy

非常重要，独有的概念。他会告诉agent，如果我在一个状态，应该采取哪一个action

直观上来看，没一个Policy运动状态都对应一个箭头，基于这些策略，我们就可以得到path，绿色的箭头告诉我们，我们在哪个位置应该做什么，在复杂情况下，我们就可以针对这个策略在某一条件下，任何一个action，采取他的概率是多少，针对一个状态，概率之和应该为1.对每个状态都应该要有对应的策略。

五、Reward

这是非常独特的一个概念，他是个数，标量，在agent采取了一个动作之后，就会得到一个数，这个数是正数，就是鼓励，负数就是对行为的惩罚。如果不给reward,或者设置为0，其实在一定程度上就会是鼓励。在数学技巧上，这个正负和鼓励和惩罚没有必然的关系，可以通过数学技巧来改变。

那么在这个网格世界中我们就可以如此设计：

如果agent想要离开这个边界，那就会给一个负数，r bound = -1，如果进入forbidden里面，也给-1，如果进入目标，就给1，其他都给0.那么设计reward，就可以实现我们的目标。我们也可以用条件概率来表示：

$p(r=-1|s_1,a_1)=1\mathrm{~and~}p(r\neq-1|s_1,a_1)=0$

在s1的情况下，采取a1的行动，reward为-1，概率为1，

六、Trajectory and Return

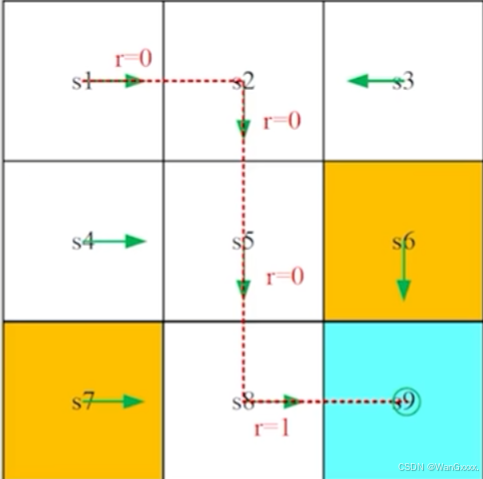
实际上是一个叫做 state-action-reward的链，考虑上图这样的trajectory

$s_1\xrightarrow{a_2}s_2\xrightarrow{a_3}s_5\xrightarrow{a_3}s_8\xrightarrow{a_2}s_9$

这就包含了三个概念，还有一个return，这个return，就是沿着这个 trajectory所得到的所有reward加起来，这里的return就是1。

分析多个trajectory 和 policy，根据return，我们就能知道哪个更好。

七、Discounted return

在上面一小节，我们看到了一条trajectory,但是这个点在最后是会一直呆在原地的，所以

$s_1\xrightarrow{a_2}s_2\xrightarrow{a_3}s_5\xrightarrow{a_3}s_8\xrightarrow{a_2}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}s_9\ldots$

那么这个return就会使无穷，在原地等待。引入Discounted rate，这个其实和深度学习的正则化系数有异曲同工之妙，为了防止数值爆炸，我们将这个rate当作系数乘以每个s，得到

$\begin{aligned}discountedreturn&\begin{aligned}&=0+\gamma0+\gamma^20+\gamma^31+\gamma^41+\gamma^51+\ldots\end{aligned}\\&=\gamma^{3}(1+\gamma+\gamma^{2}+\ldots)=\gamma^{3}\frac{1}{1-\gamma}.\end{aligned}$