为什么Harris角点检测用特征值？为什么Harris像素值变化量矩阵代表椭圆？【OpenCV】【计算机视觉】-优快云博客

本文链接：https://blog.youkuaiyun.com/Art_Smart/article/details/105462761

1. 关于Harris角点检测采用特征值作为判定标准的思考

窗口滑动的像素灰度值变化函数E的方程实际上是二次型（网上很多文章介绍该函数的具体形式和由来，这里不再赘述，见参考资料1）。主对角线元素（特征值）恒大于零且不相同，那么该二次型代表的是椭圆。二次型中间矩阵特征值分解后，对角矩阵代表对圆的伸缩，两边正交矩阵代表对椭圆的旋转（参考马同学对特征值分解的介绍）。两个特征值分别对应椭圆的长轴、短轴。两个特征值分别是椭圆长、短轴平方的倒数。即轴长度与特征值成反比例关系（计算一下标准椭圆的二次型矩阵就明白了）。
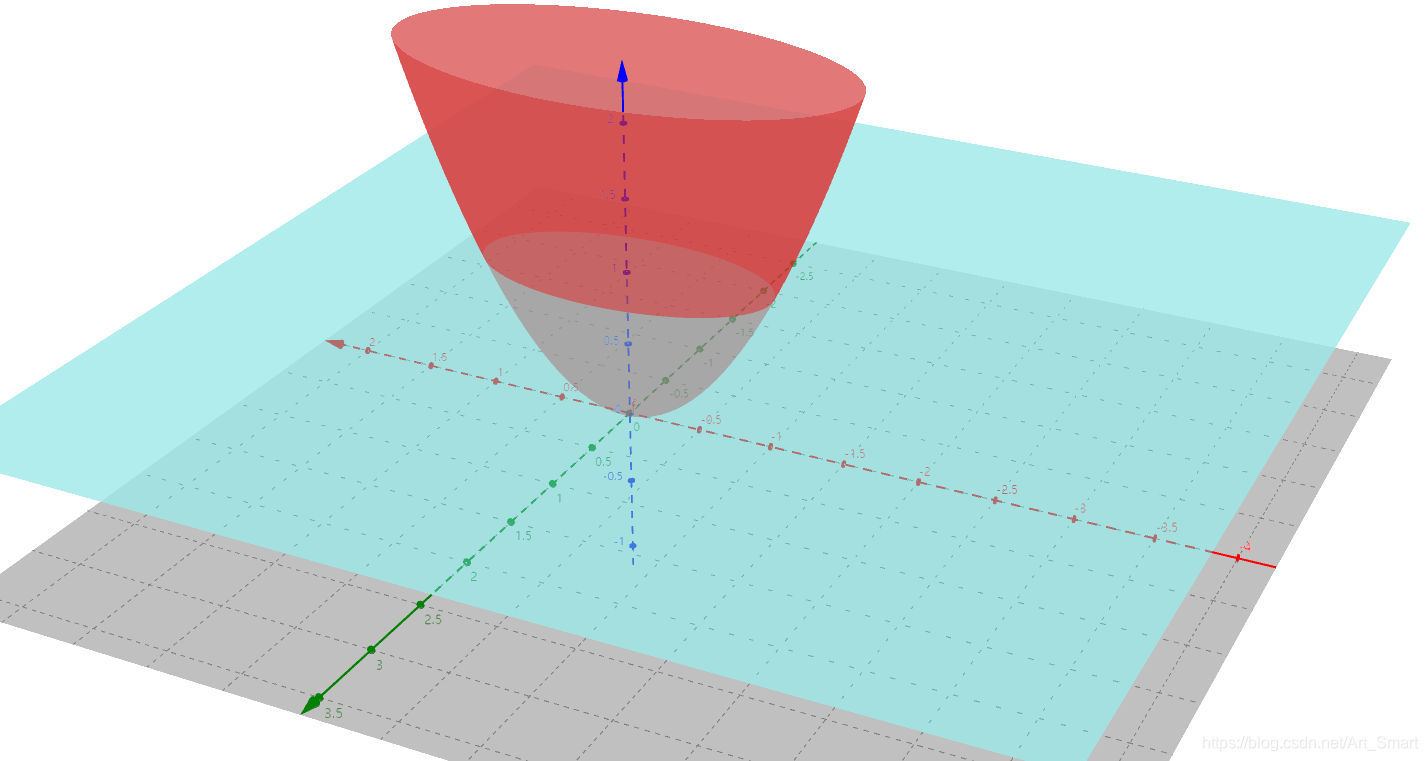
在这里插入图片描述

图中红色图像是灰度值变化函数 E 的图像，其形状类似倒立的圆锥体，但是每一个水平截面都是椭圆曲线（非实心椭圆区域），且长、短轴正比于sqrt(z)。灰色平面是 X-Y 平面。蓝色平面是 Z=c（常数）即 E=c 平面。

假定给定灰度值变化量，即令函数E=c（常数）。该二次型函数变成一个椭圆方程。如下图：
在这里插入图片描述
此时，该二次型代表以偏移量（u，v）为变量的椭圆区域。椭圆短轴的地方，代表像素值变化最剧烈的方向，因为得到相同灰度变化值所需的偏移量最小；长轴的地方，代表像素值变化最缓慢的地方，因为得到相同灰度变化值所需的偏移量最大。

椭圆长短轴分三种情况：
（1）如果长短轴都很大且相近，代表着所有方向的变化都很缓慢，证明窗口在平坦区域；
（2）如果长轴很长，断轴很短，代表在单一方向像素值变化快，其他方向像素值变化慢，证明窗口内包含边缘；
（3）如果长、断轴都很小且相近，代表两个（多个）方向的像素值变化都很快，证明窗口内包含角点。

2. 为什么Harris矩阵M代表的二次型一定是椭圆呢？

我们知道二次型与圆锥曲线密切相关。
M矩阵进行特征分解后的两个特征值为
$\lambda_{1} , \lambda_{2}$

对角矩阵
$\begin{bmatrix} \lambda_{1} &0 \\ 0 & \lambda_{2} \end{bmatrix}$
表征M代表的图形的具体形状，而单位正交特征向量矩阵则代表对该形状的旋转。两个特征值分别是椭圆长、短轴平方的倒数。

要证明M矩阵代表的必定是椭圆，需要证明如下两条：
1、M矩阵有两个不同的特征值，那么M才有两个正交的特征向量。
2、M矩阵的两个特征值均大于0。（这条和椭圆方程形式有关，若一正一负表示双曲线。均为负，该二元二次函数代表的图像与平行于X-Y平面的截面也是椭圆，只不过图像在X-Y平面下方，其函数值为负，与Harris中用二次型代表窗口滑动后像素点灰度值变化程度相悖，因为该程度取欧氏距离（L2范数）的平方，恒为正。）

M矩阵为
$\begin{bmatrix} A &B \\ B & C \end{bmatrix}$
其中A、B、C分别为：
$A=\sum_{m}I_{x_{m}}^{2} \ \ ,C=\sum_{k}I_{y_{k}}^{2}\ \ ,B=\sum_{i}I_{x_{i}} I_{y_{i}}$
其中，Ixi表示窗口在（xi,yi）点处像素值对x轴的偏导数。
由A、B、C的定义可知，A>0，C>0。

3. 证明：M矩阵有两个不同的特征值。

有特征值与矩阵行列式、迹的关系知：
$\lambda_{1}·\lambda_{2}=AC-B^{2}\ (1)\ ,\lambda_{1}+\lambda_{2}=A+C\ (2)$
上述两式带入可得特征方程为：
$\lambda^{2}-(A+C)\lambda+(AC-B^{2})=0$
该方程有两个不同解的充要条件是：
$\Delta=(A+C)^{2}-4(AC-B^{2})=(A-C)^{2}+B^{2}>0$
上式显然成立，所以M必有两个不同特征根。

4. 证明：M矩阵的两个特征值均大于0

$\lambda_{1}·\lambda_{2}=AC-B^{2}=\sum_{m}I_{x_{m}}^{2} ·\sum_{k}I_{y_{k}}^{2}-\sum_{i}I_{x_{i}}^{2} I_{y_{i}}^{2}=\sum_{i\ \neq j}I_{x_{i}}^{2} I_{y_{j}}^{2}>0$
上式显然成立。
$\lambda_{1}+\lambda_{2}=A+C=\sum_{m}I_{x_{m}}^{2}+\sum_{k}I_{y_{k}}^{2}>0$
上式显然成立。
可得不等式方程组：
$\left\{\begin{array}{l}\lambda_1+\lambda_2>0\\\lambda_1\cdot\lambda_2>0\end{array}\right.$
该不等式方程组代表的空间为：
$\left\{\begin{array}{l}\lambda_1>0\\\lambda_2>0\end{array}\right.$
所以，M矩阵两个特征值恒为正。