笔记_Prognosis_week2

一. Tree-based model
a) Decision tree

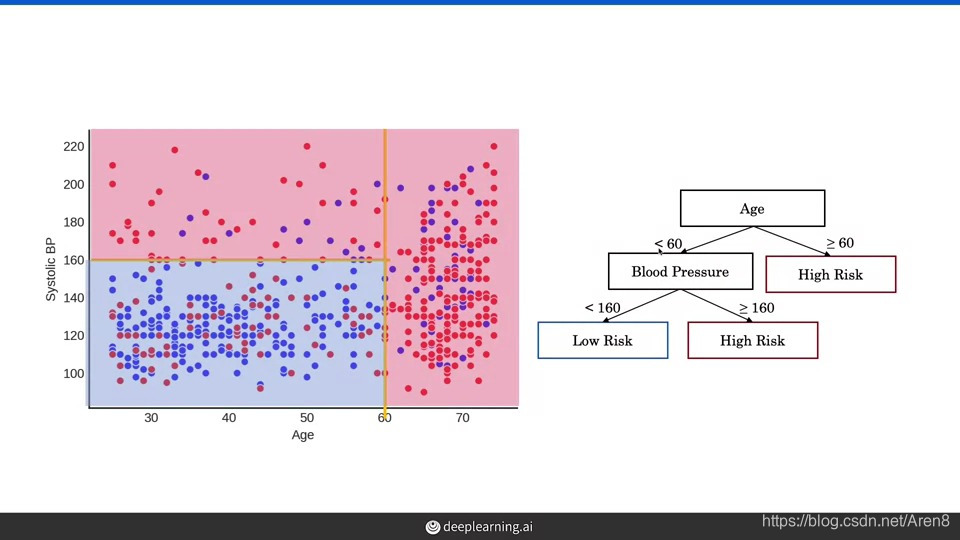
• Decision tree boundaries are always vertical or horizontal.

• Decision trees can model nonlinear associations. Notice how they’re
  able to capture here that the risk is low when both age and BP are
  low.

• The step of building a decision tree is to pick a variable and a
  value of that variable that partitions the data, such that one
  partition contains mostly red and the other partition contains
  mostly blue.
  
  b) Random forest

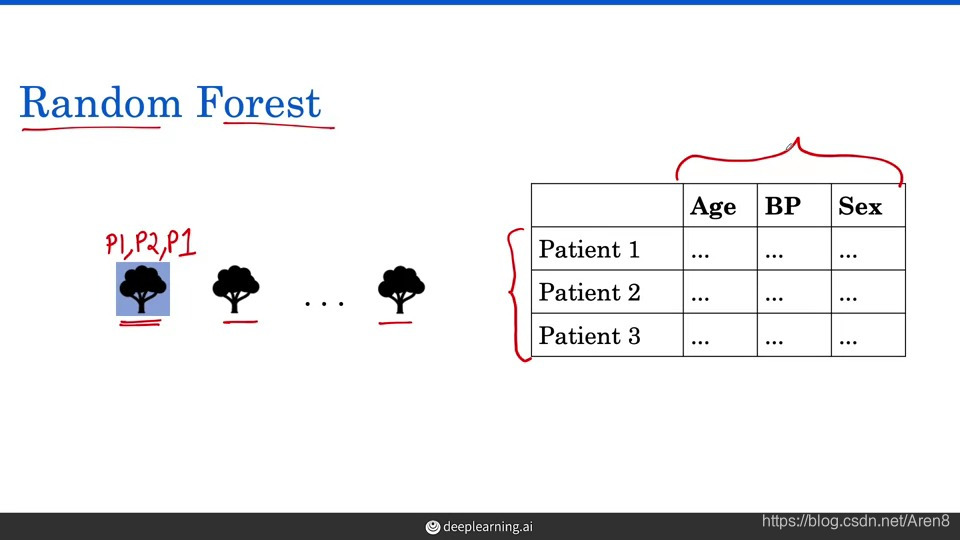
• First, each tree in the forest is constructed using a random sample
  of the patients. For instance, for the first tree, we might draw P1,
  P2, P1, which can happen because the random forest samples with
  replacement.

• Second, the random forest algorithm also uses a subset of features
  when creating decision boundaries.

• With these two key concepts, a random forest algorithm learns to
  build multiple decision trees on given data. And the random forest
  takes the simple average of those risk as the risk prediction.

• Random forests are called an ensemble learning method. There are
  other popular algorithms that use ensembles including Gradient
  Boosting, XGBoost, and LightGBM which are also able to achieve high
  performance when working with structured data in medicine and in
  other domains.
  
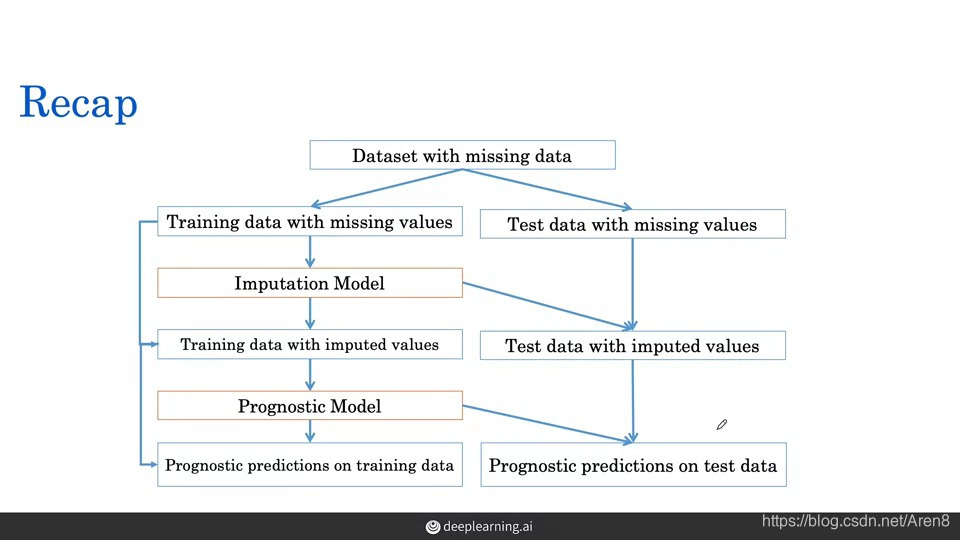
  二. identify missing data

• Problem: New test set with the same study design comes with no
  missing data. Our random forest model performs poor on this new test
  data set.

• The reason why missing data is common in medical field: One reason
  this might happen is in the clinic, physicians may not regularly
  record blood pressure for young patients but might be a routine part
  of care for older patients. And there are a lot of patterns like this
  which can generate a systematic missingness to the data.

• The reason why random forest model performs poor: the distribution of
  previous data set and the new data set are different. As the figure
  shows, we got to eliminating a lot of young patients (the missing group) after dropping. So, we’re performing poorly on patients that are younger (the missing group) but we don’t know it when we using the data after dropping.
  
  三. Missing data category:

• Missing completely at random: flip the coin to decide whether to
  record the BP, this will not lead to bias model.

• Missing at random: when the patient is younger than 60, flip the coin
  to decide whether to record the BP(So missing at random is when
  missingness depends only on the available information).

• Missing not at random: when there are patients waiting, flip the coin
  to decide whether to record the BP (It would be something that would be unobservable in the data——whether there are patient waiting)

  ##we cannot be sure what the cause of the missing data##

四. Imputation——fill in the missing data by estimation

1. Use the mean value of the training data to fill in the blank of the training data and testing data
2. Use regression: fit a linear model to the training set and apply it to the test set