Second-order consensus for nonlinear leader-following multi-agent systems via dynamic output feedback control
写在前面
从今天开始,就要开始记录每天读的论文,思路,公式的推导以及其他的一些乱七八糟的东西了。希望能坚持下去吧。如果对文章有任何问题,或者想与我交流,欢迎加我的qq649660368注明来意,谢谢。
摘要

摘要主要讲的是,论文研究了一个非线性领航跟随系统的二阶共识问题。为了解决无法测量智能体的速度,以及非线性部分未知的情况,设计了一种基于观测器的动态输出反馈控制器,并且这是基于非分离原则的。使用这种反馈控制技术,当选择了合适的增益以后,可以看到系统的输出达到了共识。并且文章还给出了两个例子用来验证控制器的有效性。
这里的non-separation principle通过后续的证明,大概意思就是无法进行变量的分离。
准备工作
问题描述

这里的(1)式描述的就是领航跟随系统的每一个智能体。很好理解,状态(位姿)的导数是速度,速度的导数由
f
(
t
i
,
x
i
,
v
i
)
f(t_i,x_i,v_i)
f(ti,xi,vi)以及
u
u
u来决定,它们分别为系统的非线性部分,以及系统的控制量输入,根据现控的基本知识,很明显
u
u
u即为我们需要设计的部分。
同时问题也规定了领航者的指定轨迹,通过加
d
d
d来描述。这里我们认为这些数学符号均为已知量。
图论


这里主要向读者普及了一下图论的基本知识。在我第一遍阅读的时候在这个位置卡了比较久的时间。所以可以考虑去百度一下相关的一些知识,都是非常常用的图论知识。这里作一个简要的说明。
首先对于一张图来说,可以通过
G
=
{
V
,
E
,
A
}
G=\lbrace V,E,A\rbrace
G={V,E,A}来描述。
V
V
V是图中顶点的集合,
E
E
E为边的集合,两个顶点之间若有联系,则这个联系就是边。
A
A
A是图的邻接矩阵(这里可以直接百度一下,说的应该比我好)。同时也定义了图的度矩阵,或者说出度矩阵
D
D
D,并且定义拉普拉斯矩阵为
L
=
D
−
A
L=D-A
L=D−A,这个矩阵在其他多智能体一致性论文里也会经常出现。定义了若图是联通的,那就是对任意两个节点之间都有一条路径。
同时我们假设
v
0
v_0
v0是领航者。下文中被标签为下标0的,都是领航者相关的部分。领航者与跟随者之间的联系是单向的,都是领航者向跟随者发布自己的位姿信息,而不会反过来接收跟随者的位姿。我们认为若跟随者与领航者有联系,则
b
i
>
0
b_{i}>0
bi>0,反之等于0,这样的矩阵为
B
B
B。
假设与引理

第一条假设是对非线性的部分作了一定的条件约束。第二条则是假设图是连通的,即任意两个节点之间至少有一条路径连通。
第一条引理和拉普拉斯矩阵
L
L
L有关,直接使用就好,第二条是认为若图是联通的,则
L
+
B
>
0
L+B>0
L+B>0。
正文


首先文章给出了控制器和观测器的具体设计,以及一些参数的取值范围。直接看文中的3,4,5会比较蒙,阅读的顺序应该为先看其推导过程,再回过来看这个控制器的结构。
证明如下:

首先定义了两个误差量,分别是对领航轨迹和速度的误差。
然后给出了根据误差的符号(上面加一个横线),给出了跟随者的状态空间表达式。这里的(7)只要把(1)和(2)直接相减就可以得到。然后对控制器的证明由下面的两个步骤完成。第一个步骤是状态反馈控制器的设计,第二个步骤为设计分布式的状态观测器。这里的分布式我觉得就是给每个跟随者都配同一个观测器的意思。
step1:状态反馈控制器设计

这里定义了李雅普诺夫函数,下面的step1的工作都围绕着该函数的导数负定去解决。同时定义了
ξ
\xi
ξ方便后面的描述。这里的带入都是一些展开。

式12是将非线性的部分缩写,用
f
‾
i
\overline{f}_i
fi来表示。这里同样是一些带入的操作。
13式是对12和11的一个整合。没有太大的意义。
14式是对非线性的部分做一些放缩处理。这里使用了两次基本不等式。
第二行到第三行用到了
∣
a
+
b
∣
≤
∣
a
∣
+
∣
b
∣
|a+b|\leq|a|+|b|
∣a+b∣≤∣a∣+∣b∣
黄字部分是我第一遍没有理解的部分。后来发现是对前面那个
2
ρ
∣
x
‾
i
∣
∣
ξ
i
∣
2\rho|\overline{x}_i||\xi_i|
2ρ∣xi∣∣ξi∣的一次基本不等式。正向看可能不太容易,将答案反推,就能得到它是由什么式子展开的了。(latex还是太方便敲公式。第一遍忘了保存关掉了。所以这里讲的很省略,本来就是为了自己整理一下思路而写的博客,所以哈哈哈大家自己理解一下就好了,应该很容易才对。)

15式也是对前面阶段性的整理,并且将公式用向量来描述。
16是直接给出了作者设计的控制器。
第二个等式是将上面的
ξ
i
\xi_i
ξi展开,同时也将
∣
x
‾
i
∣
,
∣
v
‾
i
∣
|\overline{x}_i|,|\overline{v}_i|
∣xi∣,∣vi∣展开得到。问题可能在找不到
x
d
,
v
d
x_d,v_d
xd,vd,但是明显全都展开再整理以后可以得到16式。
17是将所有的16式组合起来,通过矩阵表示。
问题可能在不知道什么表示什么。
这里给出一点小小的提示:
∑
j
∈
N
i
a
i
j
(
x
i
−
x
j
)
=
L
x
‾
\sum_{j\in N_i}a_{ij}(x_i-x_j)=L\overline{x}
∑j∈Niaij(xi−xj)=Lx,其他的自己去考虑了哈。我就不打了。把16式拆成四个部分而已。

这里的17带入15,但是其实他作了这样一个操作再带入
u
=
u
−
u
s
+
u
s
u=u-u_s+u_s
u=u−us+us
然后再做的带入。
结合下面19式得到的结论就可以得到了。
这里的黄色部分,是选择了一个合适的k值,来保证
V
s
˙
\dot{V_s}
Vs˙的负定。
这里的推导省略了。
2
ρ
2
+
ρ
+
1
−
k
(
L
+
B
)
≤
0
2\rho^2+\rho+1-k(L+B)\leq0
2ρ2+ρ+1−k(L+B)≤0
k
(
L
+
B
)
≥
2
ρ
2
+
ρ
+
1
k(L+B)\geq2\rho^2+\rho+1
k(L+B)≥2ρ2+ρ+1
通过公式可以得到19式的条件。
λ
m
i
n
(
L
+
B
)
\lambda_{min}(L+B)
λmin(L+B)是求后面括号矩阵的最小特征值。在这里应该是一个矩阵方面的不等式结论。我没有查到也没有学过,学艺不精,但是论文里面写了,应该就是对的吧,看着就很有道理。
在得到了19式的结果后,我们就可以得到,可以达到系统的全局共识,也就是这里的控制量输入
u
=
u
x
u=u_x
u=ux的时候。
step2:分布式观测器的设计

定义两个新的量
θ
i
,
η
i
\theta_i,\eta_i
θi,ηi,并且认为
θ
^
,
η
^
\hat{\theta},\hat{\eta}
θ^,η^是他们的估计值,也就是实际可以测量得到的值。
21式的左边是正常的对
θ
i
,
η
i
\theta_i,\eta_i
θi,ηi的求导。而后面的估计误差乘一个系数
l
l
l则是观测器的基础操作。不明白的可以回去看看线性系统理论方面的观测器的设计。这里的
l
l
l为待调的参数。
22式是换汤不换药的继续组合+矩阵表示,和17差不多,上面理解了,下面就没问题了。
23 24式需要时间自己看一下,就是简单的求导+带入。

25式就是对21的组合+矩阵表达。
接下来定义两个误差量
e
1
,
e
2
e_1,e_2
e1,e2,分别是对两个量的观测误差。
通过23和25式,可以求导并整理得到27的结论。这里我也自己推过一遍,证明他是对的,这里用到了
e
2
e_2
e2下面的那个奇怪的
l
l
l。没有用到什么新的公式。

28式给出的是观测器的李雅普诺夫函数。接下去的理解和推导还是有不小的难度的。
首先29式第一行是直接对28的求导,并且将27的结论带入并做一些整合。细心一点可以得到论文相同的结果,没有问题。
第三行是将上面的 1,4,7消去,2,5组合,得到公式的前两项。并且做了两次基本不等式。
对
2
(
−
1
2
e
1
T
(
L
+
B
)
)
∗
(
1
2
F
‾
l
)
≤
1
2
e
1
T
(
L
+
B
)
2
e
1
+
F
‾
2
F
‾
2
l
2
2(-\sqrt{\frac{1}{2}}e_1^T(L+B))*(\sqrt{\frac{1}{2}}\frac{\overline{F}}{l})\leq\frac{1}{2}e_1^T(L+B)^2e_1+\frac{\overline{F}^2\overline{F}}{2l^2}
2(−21e1T(L+B))∗(21lF)≤21e1T(L+B)2e1+2l2F2F
同样的方法可以得到下面那一项。
第五行就是做了一个合并,这里用到的
λ
m
a
x
[
(
L
+
B
)
]
2
\lambda_{max}[(L+B)]^2
λmax[(L+B)]2应该和19式类似用到了一个矩阵不等式方面的结论。
同样的,这里的非线性部分
F
‾
2
F
‾
\overline{F}^2\overline{F}
F2F也可以在30式进行处理缩放。
第一行是展开成级数的形式,第二行使用了假设1的公式。
第三行,先通过
ξ
i
\xi_i
ξi做的转化,然后同样用到了前面14式用到的
∣
a
+
b
∣
≤
∣
a
∣
+
∣
b
∣
|a+b|\leq|a|+|b|
∣a+b∣≤∣a∣+∣b∣。不再赘述。
第四行是先将平方展开,然后对中间带绝对值的乘法做了一个基本不等式。
至于为什么这么设计,应该有他自己的道理。
第五行为表示成矩阵形式。
31是对上面的30和29的一个整合。
通过31式这个最终结果,我们发现
V
˙
e
\dot{V}_e
V˙e的负定条件是没有办法证明出来的,因为这和
x
‾
,
ξ
\overline{x},\xi
x,ξ的取值有关。所以我们只能得到一个非分离原理的控制器。
step3:输出反馈控制器设计

这里综合step1和step2所得的结论,可以直接获取32式这个控制器。

选择了step1,2所提供的李雅普诺夫函数,进行组合得到了33。这里的
l
3
2
l^{\frac{3}{2}}
l23属于作者的技巧。
通过上面的19和31结论,我们可以快速的写出34式。
35式是下面三个组合起来的,我一起贴上,免得反反复复去找了。3和16式,


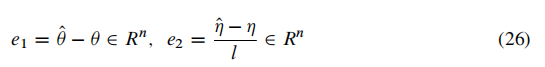
加上下面的20式

20式的后半部分可以把16式的最后
v
i
v_i
vi相关的部分转化为
η
\eta
η,从而带入得到上面的35式。
26式被用在了35到36上。小于等于左边的部分通过26式可以得到。
而右边的不等式可以通过构造基本不等式来解决。和前文思路一致,这里不再赘述。
将得到的36式带入前面总结的34式,可以直接得到37。

这里的38的获得,需要一定的时间去思考。首先想要满足
V
˙
\dot{V}
V˙负定的条件。对于
l
l
l来说需要满足两个中括号的条件。但是很明显,对于第一行的不等式,完全被第二行所包含。也就是被38式max内的第一项所包含,所以这里省略了。
同样的,对37式的第三行的公式而言,其实就对应了max的第二项。我们剩下的目标就是将37式第二行内求解出
l
l
l的条件。
假设
l
1
2
=
x
l^\frac{1}{2}=x
l21=x。
我们可以得到
x
2
−
k
2
x
−
9
λ
2
>
0
x^2-k^2x-\frac{9\lambda}{2}>0
x2−k2x−29λ>0
通过求根公式可以得到其中一个大的解是:(小的那个不符合第一行的那个结果,敲公式太麻烦被我省去了):
x
>
k
2
+
k
4
+
18
λ
2
x>\frac{k^2+\sqrt{k^4+18\lambda}}{2}
x>2k2+k4+18λ
这里又用到了一个基本不等式:
a
+
b
≥
a
+
b
\sqrt{a}+\sqrt{b}\geq\sqrt{a+b}
a+b≥a+b
所以
x
≥
k
2
+
9
λ
2
x\geq k^2+\sqrt{\frac{9\lambda}{2}}
x≥k2+29λ
这样就得到了38的结论。
然后39式给出了
V
˙
\dot{V}
V˙负定的结论。当满足上述条件以后,可以得到了。也就是文中所述
x
i
→
x
d
,
v
i
→
v
d
x_i\to x_d,v_i\to v_d
xi→xd,vi→vd,当
t
→
∞
t\to\infty
t→∞。


这里还给了三个remark,
Remark 1
文中提出的共识算法,是分布式的,信息都是邻居之间传递,所以提高了效率和鲁棒性,并且对通信的要求较小。
Remark 2
虽然考虑的多智能体系统是非线性的,但所提出的控制器和观测器都是线性的。在这里,我们不使用传统的观察者设计方法(即复制整个非线性系统)的主要原因有两个方面:(i)非线性项f./通常由于参数不确定而未知,(ii)线性观测器是更简单、更易于实现。这种观察器和控制器设计方法称为非分离原理设计方法,这里贴一篇参考文献,这里的非分离原理是针对这篇文章所说的,有机会我也会去读一下。Qian C, Lin W. Output feedback control of a class of nonlinear systems: a nonseparation principle paradigm. IEEE
Transactions on Automatic Control 2002; 47(10):1710–1715.。当然,如果它是已知的,我们可以直接为每个代理构造观察者。然后,基于分离原理,我们可以分别分析控制系统的稳定性和观察者误差系统的稳定性。在这种情况下,由于大量信息的使用,闭环系统的动态性能将会更好。
Remark 3
从定理3.1提出的增益条件可以发现,控制器/观察者增益仅由Lipschitz常数和邻接矩阵的最小和最大特征值决定。 因此,增益条件将受到通信拓扑图而不受多智能体个数的影响。
论文剩下的部分给出了两个数值的例子,作为这篇文章的支撑材料。大家去翻翻原文就好。这里就不贴了,反正我也懒得翻译。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








