[MATLAB]平台直方图算法MATLAB实现

MATLAB验证FPGA平台直方图的实现

Blog: https://blog.youkuaiyun.com/AnimateX
Email: semi_xiaobai@qq.com

---

1 直方图

在统计学中，直方图（英语：Histogram）是一种对数据分布情况的图形表示，是一种二维统计图表，它的两个坐标分别是统计样本和该样本对应的某个属性的度量。

---

2 归一化直方图

把直方图上每个属性的计数除以所有属性的计数之和，就得到了归一化直方图。之所以叫“归一”，是因为归一化直方图的所有属性的计数之和为1，也就是说，每个属性对应计数都是0到1之间的一个数（百分比）。

---

3 应用

3.1 图像直方图（英语：Image Histogram）

图像直方图是用以表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素数。可以借助观察该直方图了解需要如何调整亮度分布。这种直方图中，横坐标的左侧为纯黑、较暗的区域，而右侧为较亮、纯白的区域。因此，一张较暗图片的图像直方图中的数据多集中于左侧和中间部分；而整体明亮、只有少量阴影的图像则相反。

很多数码相机提供图像直方图功能，拍摄者可以通过观察图像直方图了解到当前图像是否过分曝光或者曝光不足。

计算机视觉领域常借助图像直方图来实现图像的二值化。

3.2 颜色直方图

在图像处理和摄影领域中，颜色直方图（英语：Color Histogram）指图像中颜色分布的图形表示。数字图像的颜色直方图覆盖该图像的整个色彩空间，标绘各个颜色区间中的像素数。

颜色直方图本身可以针对任意色彩空间使用，但这一术语通常只用在诸如 RGB 和 HSV 的三维色彩空间，而针对灰度图像时常使用亮度直方图（英语：Intensity Histogram）这一术语。

3.3 质量直方图

在质量管理领域中，质量分布图是根据从生产过程中收集来的质量数据分布情况，画成以组距为底边、以频数为高度的一系列连接起来的直方图。

---

4 直方图均衡化

直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。如下图所示为直方图均衡化的示意图。

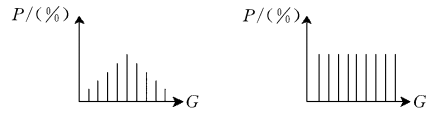
这种方法通常用来增加许多图像的全局对比度，尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法，亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

这种方法对于背景和前景都太亮或者太暗的图像非常有用，这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作，如果已知均衡化函数，那么就可以恢复原始的直方图，并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择，它可能会增加背景噪声的对比度并且降低有用信号的对比度。

---

参考书： 冈萨雷斯 数字图像处理第三版

5 理论知识

考虑连续灰度值，并用变量r表示待处理图像的灰度。r的取值范围是[0, L-1]，L代表灰度级总数。先注意变换形式（灰度映射）：

$$s=T(r), 0\leq{r}\leq{L-1}\hspace{5.5cm} (1)$$
对于输入图像中每个具有r值的像素值产生一个输出灰度值 $s$。我们假设：
(a) $T(r)$在区间 $0\leq{r}\leq{L-1}$上为单调递增函数；
(b) 当 $0\leq{r}\leq{L-1},\quad 0\leq{T(r)}\leq{L-1}$。
引出反函数：
$$r=T^{-1}(s),0\leq{s}\leq{L-1}\hspace{5cm} (2)$$
这种情况下，上面(a)假设变为：
(a) $T(r)$在区间 $0\leq{r}\leq{L-1}$上是一个严格单调递增函数。

条件(a)中要求$T(r)$为单调递增函数是为了保证输出灰度值不少于相应的输入值，防止灰度反变换时产生认为缺陷。条件(b)是保证输出灰度的范围与输入灰度的范围相同。最后新的(a)保证从$s$到$r$的映射是一对一的，防止出现二义性。

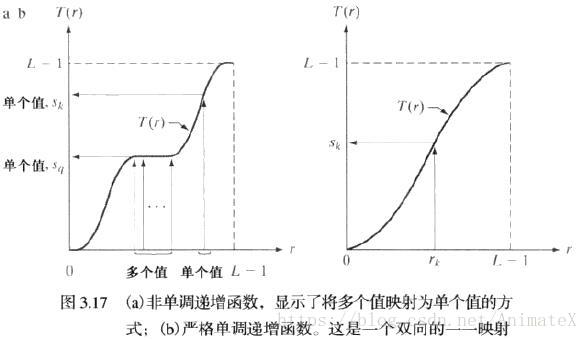
上图满足(a)和(b)两个假设，可以看出多值映射到单值也是可能的，并且仍然满足两个假设。
简单来讲， $r$到$s$映射很完美，但是我们想要唯一的从映射的值恢复 $r$值（反映射由反向箭头表示），上图(a)则存在问题。图中$s_k$的反映射是可能的，但 $s_q$反映射的是一个范围的值，通常，要防止由 $s_q$恢复原始的 $r$值的问题。如上图(b)所示，$T(r)$要求是严格单调的，以保证反映射是单值的（即两个方向上的映射都是一对一的），因为实践中我们处理的是整数灰度值，必须把所有结果四舍五入为最接近的整数值。因此，如果严格单调不满足时，我们就需要寻找最接近整数匹配的方法来解决非唯一反变换的问题。
如下图所示。

---

6 数学知识

一幅图像的灰度级可以看成是区间$[0, L-1]$内的随机变量。随机变量的基本描绘子是其概率密度函数（PDF）。令$p_r(r)$和$p_s(s)$分别表示随机变量$r$和$s$的概率密度函数，其中p的下标用于指示不同的函数。由基本概率论得到的一个基本结论就是，如果$p_r(r)$和$p_s(s)$已知，且在感兴趣的值域$T(r)$上是连续可微的，则变换后的变量$s$的PDF可由下面的简单公式得到:

$$p_s(s)=p_r(r) \left| \frac{d_r}{d_s} \right| \hspace{7.8cm} (3)$$
这样，我们看到，输出灰度变量s的PDF就由输入灰度的PDF和所用的变换函数决定。
在图像处理中特别重要的变换函数有如下形式：

$$s=T(r)=(L-1)\int^r_0p_r(w)dw \hspace{5cm} (4)$$
其中， $w$是积分的假变量。公式右边是随机变量$r$的累积分布函数（CDF）。因为PDF总为正，一个函数的积分应该是该函数下方的面积，遵循公式（4）的变换函数满足前述假设（a），因为函数下的面积不随 $r$的增大而减小。当在该等死中上限是$r=L-1$时，积分值等于1（PDF曲线下方的面积总是1），所以 $s$的最大值是（L-1），并且假设（b）也是满足的。
寻找公式（3）中相应的变换$p_s(s)$。由基本积分学中的莱布尼茨准则知道，关于上限的定积分的导数是被积函数在该上限的值，即
$$\frac{d_s}{d_r}=\frac{d_{T(r)}}{d_r}=(L-1)\frac{d}{d_r}[\int^r_0p_r(w)dw]=(L-1)p_r \hspace{1cm} (5)$$
将公式（5）带入公式（3），并记住概率密度值为正，得到
$$p_s(s)=p_r(r) \left| \frac{d_r}{d_s} \right| =p_r(r) \left| \frac{1}{(L-1)p_r(r)} \right| = \frac{1}{L-1} \hspace{1.3cm} (6)$$
$0\leq{s}\leq{L-1}$,从该公式可知, $p_s(s)$可知，这是一个均匀概率密度函数。
则知 $T(r)取决于p_r(r)$， $p_s(s)$与 $p_r(r)$形式无关。请看下面这个例子。

因为直方图是PDF近似，而且在处理中不允许造成新的灰度级，所以在实际的直方图均衡应用中，很少见到完美平坦的直方图。

---

7 代码实现

工具：MATLAB

注：本测试使用FPGA给出的灰度数据而非图片作为测试

function code

function imgOut = AHE(imgIn)
    [M, N, num] = size(imgIn);

    num_compress = 256;

    imgOut = zeros(M, N, num);


    for i = 1 : num
        % PDF
        imgTemp = round(imgIn(:, :, i));
        imgTemp = imgTemp - min( imgTemp(:) ) + 1;

        NUM = max( imgTemp(:) );

        tempPDF = zeros(1, NUM);

        % PDF: tempPDF
        for j = 1 : NUM
            tempPDF(j) = length(find(imgTemp == j));
        end
        % 计算平台值
        maxiumTempPDF = tempPDF( find( diff( sign( diff( tempPDF ) ) ) < 0 ) + 1 );

        Tmax = mean( maxiumTempPDF(:) );

        % 平台值处理
        for j = 1 : NUM
            if tempPDF(j) > Tmax
                tempPDF(j) = Tmax;
            end
        end
        % 归一化直方图
        tempPDF = tempPDF ./ (M * N);

        % CDF
        % 计算累计直方图
        tempCDF = cumsum(tempPDF);

        % HE
        % 从做开始往右对应映射
        tempH = floor( tempCDF .* (num_compress - 1) );

        % 还原数据
        for j = 1 : M
            for k = 1 : N
                imgOut(j, k, i) = tempH(imgTemp(j, k));
            end
        end
        imgOut(:, :, i) = imgOut(:, :, i) - 1;
    end
end

test code

load('objF2.mat');
figure, imshow(objF2, [ ]);
imgLF = AHE(objF2);
figure, imshow(imgLF, [ ]);

Compare
1 原始图像

2 平台直方图后的新图像

---

仅供学习！转载请提供出处！

---

参考文章：

[1]维基百科的例子不错，大家可以看看！
https://zh.wikipedia.org/wiki/%E7%9B%B4%E6%96%B9%E5%9B%BE%E5%9D%87%E8%A1%A1%E5%8C%96
[2]这个附的两个代码可以直接用的，结合前面的理论很好理解
http://www.cnblogs.com/ChenxofHit/archive/2011/02/28/1966910.html
[3]例子很直观！看图即理解
http://www.cnblogs.com/tianyalu/p/5687782.html
[4]平台直方图
http://blog.chinaaet.com/helimin/p/5100018220