背包dp相关问题

采药

思路

01背包模板代码

#include <iostream>
using namespace std;
const int N = 105,M = 1e3+10;
int f[N][M];//fij 前i个物品 在时间为j的前提下的最大值
int t[N],v[N];
int T,n;
int main() {
    cin>>T>>n;
    for(int i = 1;i<=n;i++)
    {
        scanf("%d%d",&t[i],&v[i]);
    }

    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=T;j++){
            f[i][j] = f[i-1][j];
            if(j>=t[i]){
                f[i][j] = max(f[i][j],f[i-1][j-t[i]]+v[i]);
            }
        }
    }

    cout<<f[n][T];

    return 0;
}

优化代码：
这里把条件写错了，de了好久，吐了，乌鱼子

#include <iostream>
using namespace std;
const int N = 105,M = 1e3+10;
int f[M];//fij 前i个物品 在时间为j的前提下的最大值
int t[N],v[N];
int T,n;
int main() {
    cin>>T>>n;
    for(int i = 1;i<=n;i++)
    {
        scanf("%d%d",&t[i],&v[i]);
//        cout<<t[i]<<' '<<v[i]<<endl;
    }
    for(int i = 1;i<=n;i++){
        for(int j = T;j>=t[i];j--){
                f[j] = max(f[j],f[j-t[i]]+v[i]);
//            if(j==95) cout<<f[95]<<endl;
        }
    }

    cout<<f[T];

    return 0;
}

多重背包三

单调队列优化

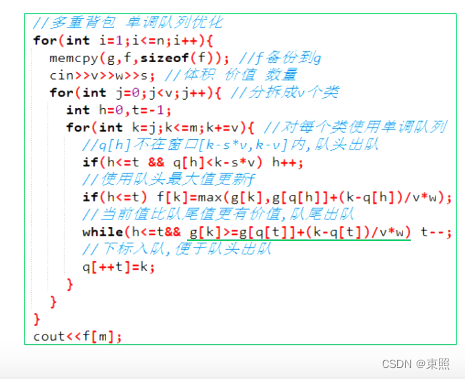
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e3+10,M = 2e4+10;
int f[M],g[M],q[M];
int main() {
    int n,m;
    cin>>n>>m;
    for(int i = 1;i<=n;i++){
        int v,w,s;
        memcpy(g,f,sizeof f);
        scanf("%d%d%d",&v,&w,&s);
        for(int j = 0;j<v;j++){
            int hh = 0,tt = -1;//每一个类都要维护一个滑动窗口
            for(int k = j;k<=m;k+=v){
                //k往后每次走v
                if(hh<=tt&&q[hh]< k-s*v) hh++;//队头不在窗口中 队头出队
                if(hh<=tt) f[k] = max(f[k],g[q[hh]]+(k-q[hh])/v*w); //用队头（最大值）去更新当前f[k]值 但是使用的是f[i-1][q[hh]]的值 所以要用g[M]存下上一排
                while(hh<=tt&&g[q[tt]]+(k-q[tt])/v*w<=g[k]) tt--;
                q[++tt] = k;
            }
        }
    }
    cout<<f[m];
    return 0;
}