算法 | 虚树学习笔记

最新推荐文章于 2024-09-29 23:10:08 发布
原创 最新推荐文章于 2024-09-29 23:10:08 发布 · 391 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文介绍了虚树的概念，包括其构建方法和最坏情况分析。通过举例说明虚树的构建过程，并提供了HDU6035 Colorful tree和HNOI2014 | 世界树两道题目的题解，展示了虚树在解决树形结构问题中的应用，如计算路径权值和确定控制点。
虚树学习笔记?

blog

  • 虚树是一棵虚拟构建的树…废话 这棵树只包含关键点和关键的点,而其他不影响虚树结构的点和边都相当于进行了路径压缩…而且整棵虚树的大小不会超过关键点的2倍

    • 举个例子？
    • 比方说…4 5 6 7 表示关键点(现在你要让这些关键点也形成一棵树…要求点最少但不能破坏原来树的结构)
    • 构建完的虚树长这个样(其实这也是构建虚树时候的最坏情况…所有原来树上的点都加入了虚树之中)
    • 什么时候才会出现这种最坏的情况???当所有叶子节点都是关键点的时候…，但是很显然的是叶子结点不会超过 n 2 \dfrac{n}{2} 2n​个

  • 如何构建虚树？

    • 预处理出dfs序…将关键点按照dfs序进行排序

    • 我们使用一个栈,从栈顶到栈底的元素形成虚树的一条树链.

    • Code

      • 	sort(af + 1, af + 1 + num, cmp);
	if(con[1] != 1) st[++top] = 1;
	for(int i = 1; i <= num; ++i) {
		int pos = af[i], fa = 0;
		for(; top;) {
			fa = GetLCA(st[top], pos);
			if(top > 1 && dep[fa] < dep[st[top - 1]]) {
				add(st[top - 1], st[top]), top--;
			} else if(dep[fa] < dep[st[top]]) {
				add(fa, st[top]), top--;
				break;
			} else {
				break;
			}
		}
		if(st[top] != fa) 
			st[++top] = fa;
		st[++top] = pos;
	}
	for(; top > 1; --top)
		add(st[top - 1], st[top]);

  • 正确性✅?

    • 对于任意指定两点 a , b a,b a,b 的 l c a lca lca ，都存在 d f s dfs dfs 序连续的两点 u , v u,v u,v( d f n [ u ] ≤ d f n [ v ] dfn[u]\leq dfn[v] dfn[u]≤dfn[v]) 分别属于 l c a lca lca包含 a , b a,b a,b 的两棵子树，此时这 v v v 加入时按照上面的操作必定会把 l c a lca lca加入栈，所以应当加入的点都加入了。对于非 l c a lca lca 点，按照上面操作是不会出现这个点的。
HDU6035 Colorful tree

  • 题意：

    • 给你一棵 n ( 1 ≤ n ≤ 200000 ) n(1\leq n\leq 200000) n(1≤n≤200000)个节点的树…每一个节点有一个颜色.一条路径的权值定义为出现颜色集合的大小…问所有路径的权值和是多少…

  • 题解:

    当我们在考虑这个问题怎么求的时候…我们很容易地考虑到要计算每个颜色的贡献

    我们会发现这样正着做会很难…遇难则反

    • 问题转换为求有多少条路径没有出现过颜色 c c c

    事实上我们并不需要构建出每一种颜色的虚树… 只需一遍dfs就可以考虑啦！

    但是应用到了虚树的思想…

    首先一个颜色没有 c o l col col的联通块里任意两个点的路径上都不会出现 c o l col col这个颜色

    我们记录一个 s u m [ x ] sum[x] sum[x]表示遍历到当前这个点 颜色为 x x x的最高子树总大小。

    假设当前点为 n o w now now,那么接下去就要遍历它的儿子…

    • 我们记下遍历每个儿子之前的 s u m [ c o l [ n o w ] ] sum[col[now]] sum[col[now]]值为 l a s t last last
    • 那么遍历完当前儿子之后 a d d = s u m [ c o l [ n o w ] ] − l a s t add=sum[col[now]] - last add=sum[col[now]]−last就是这个儿子顶部颜色为 c o l [ n o w ] col[now] col[now]的个数
    • 那么 s z [ s o n ] − a d d sz[son]-add sz[son]−add就是颜色不为 c o l [ n o w ] col[now] col[now]的联通块大小

  • Code

    #include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 10;
struct data {
	int nt, to;
} a[N << 1];
ll ans;
int sz[N], vis[N], head[N], col[N], sum[N], cnt = 0;

void add(int x, int y) {
	a[++cnt].to = y;
	a[cnt].nt = head[x];
	head[x] = cnt;
}

ll js(ll x) {
	return x * (x - 1) / 2;
}

void dfs(int u, int fa) {
	sz[u] = 1;
	int son = 0;
	for(int i = head[u]; i; i = a[i].nt) {
		int to = a[i].to;
		if(to == fa) {
			continue;
		}
		int last = sum[col[u]];
		dfs(to, u);
		sz[u] += sz[to];
		int now = sum[col[u]] - last;
		ans -= js(sz[to] - now);
		son += sz[to] - now;
	}
	sum[col[u]] += son + 1;
}

int main() {
	int n, cas = 0;
	while(scanf("%d", &n) == 1) {
		cnt = ans = 0;
		int tot = 0;
		for(int i = 1; i <= n; ++i) {
			scanf("%d", &col[i]);
			if(!vis[col[i]]) {
				tot++, vis[col[i]] = 1;
			}
		}
		for(int i = 1, x, y; i < n; ++i) {
			scanf("%d%d", &x, &y);
			add(x, y), add(y, x);
		}
		ans = 1ll * tot * js(n);
		dfs(1, 0);
		for(int i = 1; i <= n; ++i) {
			head[i] = 0;
			if(vis[col[i]]) {
				// printf("%d %d\n", col[i], sum[col[i]]);
				ans -= js(n - sum[col[i]]);
				vis[col[i]] = 0;
				sum[col[i]] = 0;
			}
		}
		++cas;
		printf("Case #%d: %lld\n", cas, ans);
	}
	return 0;
}
HNOI2014 | 世界树

  • 题意

    • 给你一棵 n ( 1 ≤ n ≤ 100000 ) n(1\leq n\leq100000) n(1≤n≤100000)个节点的树 每次给你 n u m ( ∑ n u m ≤ 100000 ) num(\sum num \leq 100000) num(∑num≤100000)个控制点

      • 一个点的控制点是离它最近的且标号最小的点

      问你每个控制点控制了多少个点

  • 题解

    首先肯定是对这个 n u m num num个点构建虚树

    先预处理出虚数上的点的控制点 在去更新原树上的控制点

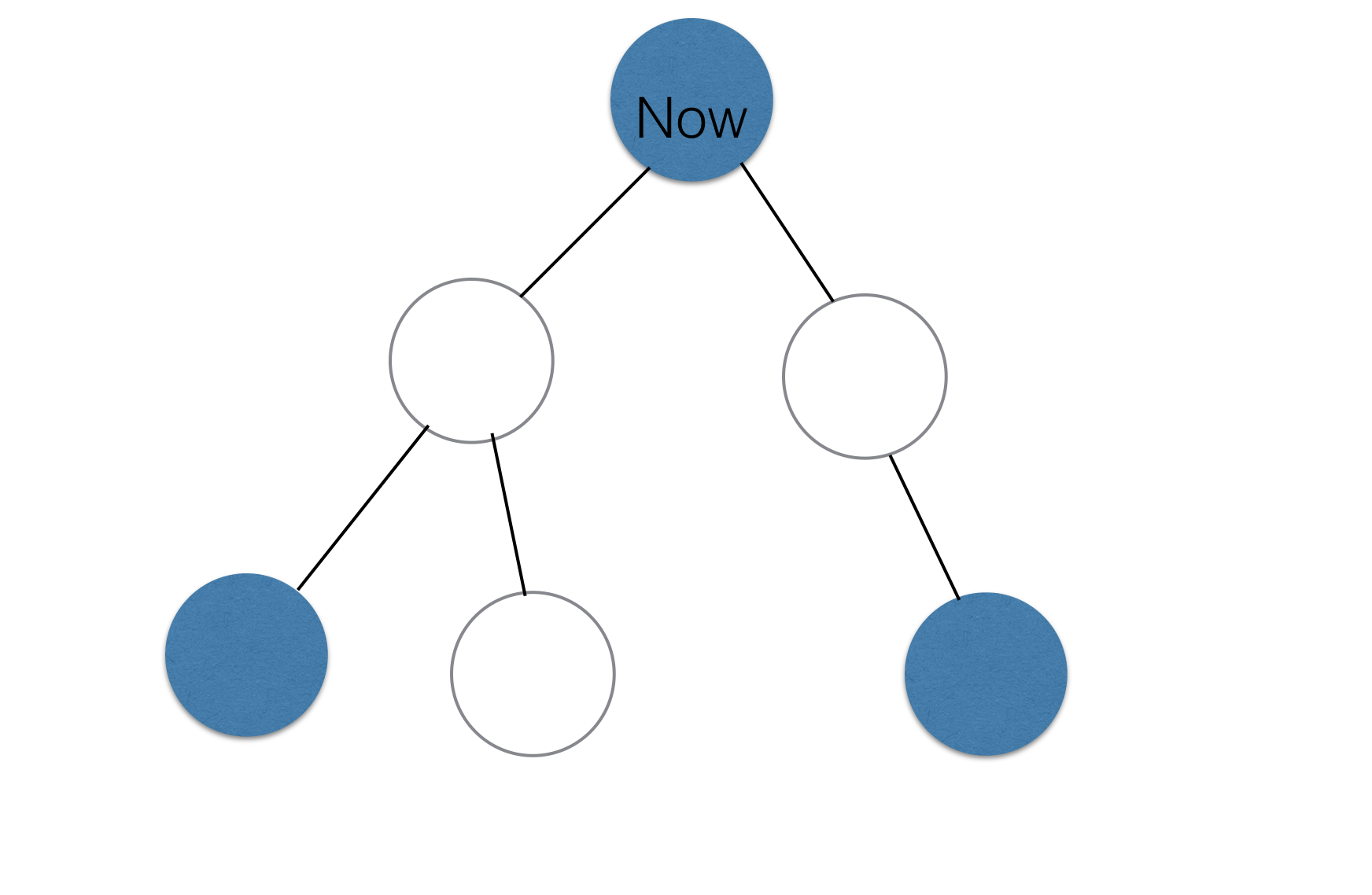
    (蓝色点为虚树上的点)有这么两种情况

    • 这两个点的控制点是一样(假设为 c o n [ x ] con[x] con[x]) 那么这两个点之间的所有点的控制点显然都是 c o n [ x ] con[x] con[x]

    • 这两个点的控制点是不一样的假设为 c o n [ x ] , c o n [ y ] con[x],con[y] con[x],con[y]

      首先倍增出 m i d mid mid点 再根据 c o n [ x ] , c o n [ y ] con[x],con[y] con[x],con[y]的大小判断距离相同时的情况

  • Code

    #include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10, LOG = 20;
struct data {
	int nt, to;
} a[N << 1];
int con[N], f[N], be[N], af[N], st[N], rem[N], c[N];
int head[N], g[N][LOG + 1], dep[N], sz[N], dfn[N];
int n, cnt = 0, res = 0, now = 0, top = 0;

void add(int x, int y) {
	a[++cnt].to = y;
	a[cnt].nt = head[x];
	head[x] = cnt;
}

void predfs(int x, int fa) {
	dfn[x] = ++res;
	dep[x] = dep[fa] + 1;
	sz[x] = 1, g[x][0] = fa;
	for(int i = head[x]; i; i = a[i].nt) {
		int to = a[i].to;
		if(to == fa) {
			continue;
		}
		predfs(to, x);
		sz[x] += sz[to];
	}
}

void prepare() {
	for(int j = 1; j <= LOG; ++j)
		for(int i = 1; i <= n; ++i)
			g[i][j] = g[g[i][j - 1]][j - 1];
}

int GetLCA(int A, int B) {
	if(dep[A] > dep[B]) 
		swap(A, B);
	for(int i = LOG; i >= 0; --i)
		if(dep[g[B][i]] >= dep[A])
			B = g[B][i];
	if(A == B)
		return A;
	for(int i = LOG; i >= 0; --i)
		if(g[A][i] != g[B][i])
			A = g[A][i], B = g[B][i];
	return g[A][0];
}

int dis(int x, int y) {
	return dep[x] + dep[y] - 2 * dep[GetLCA(x, y)];
}

void dfs(int x) {
	c[++now] = x, rem[x] = sz[x];
	for(int i = head[x]; i; i = a[i].nt) {
		int to = a[i].to;
		dfs(to);
		if(!con[to]) continue;
		int d1 = dis(x, con[to]), d2 = dis(x, con[x]);
		if((d1 == d2 && (con[to] < con[x])) || d1 < d2 || !con[x])
			con[x] = con[to];
	}
}

void Dfs(int x) {
	if(!con[x]) return ;
	for(int i = head[x]; i; i = a[i].nt) {
		int to = a[i].to;
		int d1 = dis(to, con[to]), d2 = dis(to, con[x]);
		if((d1 == d2 && (con[x] < con[to])) || d1 > d2 || !con[to])
			con[to] = con[x];
		Dfs(to);
	}
}

void work(int x, int y) {
	int ny = y, mid = y;
	for(int i = LOG; i >= 0; --i)
		if(dep[g[ny][i]] > dep[x])
			ny = g[ny][i];
	rem[x] -= sz[ny];
	if(con[x] == con[y]) {
		f[con[x]] += sz[ny] - sz[y];
		return ;
	}
	for(int i = LOG; i >= 0; --i) {
		int nxt = g[mid][i];
		if(dep[nxt] <= dep[x]) continue;
		int d1 = dis(con[x], nxt), d2 = dis(con[y], nxt);
		if(d1 > d2 || (d1 == d2 && con[y] < con[x])) mid = nxt;
	}
	f[con[x]] += sz[ny] - sz[mid];
	f[con[y]] += sz[mid] - sz[y];
}

bool cmp(int x, int y) {
	return dfn[x] < dfn[y];
}

void go() {
	now = cnt = top = 0;
	int num;
	scanf("%d", &num);
	for(int i = 1; i <= num; ++i) {
		scanf("%d", &be[i]);
		con[be[i]] = be[i], af[i] = be[i];
	}
	sort(af + 1, af + 1 + num, cmp);
	if(con[1] != 1) st[++top] = 1;
	for(int i = 1; i <= num; ++i) {
		int pos = af[i], fa = 0;
		for(; top;) {
			fa = GetLCA(st[top], pos);
			if(top > 1 && dep[fa] < dep[st[top - 1]]) {
				add(st[top - 1], st[top]), top--;
			} else if(dep[fa] < dep[st[top]]) {
				add(fa, st[top]), top--;
				break;
			} else {
				break;
			}
		}
		if(st[top] != fa) 
			st[++top] = fa;
		st[++top] = pos;
	}
	for(; top > 1; --top)
		add(st[top - 1], st[top]);
	dfs(1), Dfs(1);
	for(int i = 1; i <= now; ++i)
		for(int j = head[c[i]]; j; j = a[j].nt)
			work(c[i], a[j].to);
	for(int i = 1; i <= now; ++i)
		f[con[c[i]]] += rem[c[i]];
	for(int i = 1; i <= num; ++i) 
		printf("%d ", f[be[i]]);
	puts("");
	for(int i = 1; i <= now; ++i)
		head[c[i]] = con[c[i]] = f[c[i]] = rem[c[i]] = 0;
}

int main() {
	scanf("%d", &n);
	for(int i = 1, x, y; i < n; ++i) {
		scanf("%d%d", &x, &y);
		add(x, y), add(y, x);
	}
	predfs(1, 0), prepare();
	memset(head, 0, sizeof head);
	int m;
	scanf("%d", &m);
	for(int o = 1; o <= m; ++o) {
		go();
	}
	return 0;
}
虚树详解
tylon2006的博客
11-30 864
虚树大意：通过建一棵只包含询问点和不超过询问点数减一个lca的树来减少点的个数，降低时间复杂度 这东西不难，常用于辅助树形dp，难点在于dp… 使用该算法的标志为不确定组的询问次数与给出的询问点数和 例如： 每次询问w个数，∑i=1qwi=300000\sum_{i=1}^qw_i=300000\quad∑i=1q​wi​=300000 算法： 构建过程十分简单，放心食用 举个例子：P2495 ...
【算法竞赛学习笔记】树分治
SC_Linno的博客
03-16 660
title : 树分治 date : 2021-8-25 tags: ACM,图论 author : Linno 树分治 树分治是再树形结构上进行分治的一种操作，主要思想是除去树中的某些对象，使原树被分解成若干个互不相交的部分，由此可以解决许多以路径为询问对象的问题。 一颗树上的路径有经过根节点的或者不经过根节点的两种。 若我们把根节点删掉，则可以生成若干棵以原根节点的儿子为根节点的子树。 问题引入 给一颗带边权树，统计最短距离不超过k的顶点的对数。 解法 假设我们按重心把树分成若干子树，那么符合条件的.
虚树学习笔记
forever_shi的博客
11-17 241
全机房的小伙伴们都早就会虚树了，就我不会，于是决定学习一下虚树。前两天看了一些别人的讲解，大体明白了虚树的思想，于是写一篇学习笔记。 虚树经常用来解决在一棵树上选出若干点，有若干次询问，每次询问求这若干点的某一个东西，一般选出的点的总数是1e5量级的。这类题的一个暴力做法通常是可以对于每次询问都暴力树形dp，但是这样复杂度就比较高，我们发现每次只选出了一些点，但是却对整棵树重新做了一遍dp，看起来...
图论专题-学习笔记：虚树
Plozia 的小窝
12-01 581
图论专题-学习笔记：虚树1. 前言2. 详解2.1 虚树定义2.2 虚树构造2.3 例题3. 总结4. 参考资料 1. 前言 虚树，主要是用于一类树上问题，这类问题通常是需要取一些关键点，然后要在这些关键点和其 LCA 上做一些奇怪的玩意。 关键前置知识：LCA。 2. 详解 2.1 虚树定义 首先我们需要知道虚树是什么： 现在给出一棵 nnn 个点的树，从中选取出 kkk 个关键点，这些关键点以及其两两的 LCA 构成了对于这些关键点而言的虚树，特别注意如果取出来的树不连通的话我们还需要一个根节点来连通。
C++学习笔记与算法精要总结
从标签“C++学习笔记 C++算法”可以看出，该资料不仅涵盖了C++基础语法，还涉及了算法的实现与应用。这表明其内容不仅限于语言层面的语法知识，更注重实际编程中如何利用C++进行高效的数据结构操作与算法实现。结合...
ACM模板 | 学习笔记 树相关
风浔凌的博客
02-17 348
持续更新中qwq 咕咕咕 1 最小生成树 切割性质 假定所有边权均不相同。设S为既非空集也非全集的V的子集，边e是满足一个端点在S内，另一个端点不再S内的所有边中权值权值最小的一个，则图G的所有生成树均包含e。 回路性质。假定所有边权均不相同。设C为图G的任意回路，边e是C上权值最大的边，则图G的所有生成树均不包含e。 1.1 增量最小生成树 从包含的n个点的空图开始，依次加入m条带权边。每加入一条边，输出当前图中最小生成树权值（如果当前图不联通，输出无解）。 如果加入一条边（u,v）后，图中恰好包含一
《数据结构、算法与应用 —— C++语言描述》学习笔记 — 平衡搜索树 — 红黑树
coding-hwz
10-24 610
《数据结构、算法与应用 —— C++语言描述》学习笔记 — 平衡搜索树 — 红黑树一、基本概念 一、基本概念 红黑树是这样的一棵二叉搜索树：树中每一个节点的颜色或者是红色或者是黑色。红-黑树的其他特征可以用相应的扩充二叉树来说明： ① 根节点和所有外部节点都是黑色。 ② 在根至外部节点路径上，没有连续两个节点是红色。 ③ 在所有根节点至外部节点的路径上，黑色节点的数目相同。 红黑树还有另一种等价，它取决于父子节点间的指针颜色。从父节点指向黑色孩子的指针是黑色，从父节点指向红色孩子的指针是红色。另外还有： ①
《Python一行流》学习笔记8——算法
最新发布
AlianHN的博客
09-29 1554
本系列到这里就结束了，希望大家有时间的话还是去看一下原版书，相信你一定大有收获。当初在图书馆看到这本书的时候，真的是被它的简单给惊艳到了，用短短的一行代码就能实现很多强大的功能吧。
[学习笔记]虚树
weixin_33859231的博客
02-13 244
前言&&思想 一些给定树上一些点集，要处理和该点集有关的询问（例如和点集关系，点集选择限制）的题目， 很多子树没有变化，暴力没有意义。 提取出有关的点和路径，构成虚树 虚树上DP等等，难点往往在于找到非虚树部分的答案。 建立 1.暴力sort再sort LCA一般都要用，所有点按照dfn序sort，相邻两点的LCA就是所有涉及到的LCA 注意，LCA可能算重！...
虚树
Destiny
02-28 222
虚树 虚树 开个新坑，差点暴毙，开心。 虚树是什么？ ​ 虚树，顾名思义就是不真实的树，它出现在一类树形DP问题中。当你发现一道题目是在树上搞事情，多组询问、并且无法用树上莫队这种数据结构暴力维护、\(\sum k\)为多少时，恭喜你，这是一道虚树题。现在为了了解它，我们从一道经典虚树问题开始。 [SDOI2011]消耗战 题目大意 给出一棵树，每条边有一个边权。 有m...
算法学习——虚树
weixin_30470857的博客
09-15 179
虚树听起来是一个很高大上的东西，实际上实现起来是比较简单的。 大致的意思是说，对于一棵树而言，也许每次询问我们只需要用到其中的部分节点，因此如果每次询问我们要对全部的节点都做一次处理的话，显然会造成浪费，且很可能会超时。 这时就需要虚树了。 因为有些节点是完全无用的，但你又不能因此毁了原树——说不定下次询问还要用呢？ 所以我们可以提取出需要用到的部分节点，重新建一棵树。 我们把需要...
日常学习——Virtual_Tree(虚树）
digangmeng2546的博客
02-12 634
概念 虚树，顾名思义就是虚构的树，它是一种用来解决树上问题的算法，主要思想是只将原树上必要的点和它们的最近公共祖先取出来，构成一棵虚树，并保留他们在树上的相对关系。 引入 我们先来看一道题: 给定一棵n个点的树，每次询问给定一个大小为k的点集，你需要切掉一些边，使得点集中的点均不与1号点联通，而每条边都有被切掉所需的代价，你还要让总代价最小。\(2 \leqslant n \leqsla...
虚树详细讲解
weixin_45630722的博客
07-31 2983
新学虚树，写篇文章仔细地回顾一下吧。。。这玩意花了挺长时间的。 什么是虚树 虚树常常被使用在树形 dpdpdp 中，就比如这题。当一次询问仅仅涉及到整颗树中少量结点时，为每次询问都对整棵树进行 dpdpdp 在时间上是不可接受的。此时，我们建立一颗仅仅包含部分关键结点的虚树，将非关键点构成的链简化成边或是剪去，在虚树上进行 dpdpdp 。 虚树包含所有的询问点及它们之间的 lcalcalca 。显然虚树的叶子节点必然是询问点，因此对于某次含有 kkk 个点的询问，虚树最多有 kk...
知识点 - 虚树
qq_41848675的博客
09-13 483
知识点 - 虚树 解决问题类型： 利用虚树，可以对于指定多组点集 SSS 的询问进行每组 O(∣S∣log2n+f(∣S∣))O(|S|log_2n+f(|S|))O(∣S∣log2​n+f(∣S∣)) 的回答，其中 f(x)f(x)f(x)指的是对于树上有 xxx 个点的情况下单组询问这个问题的时间复杂度。可以看到，这个复杂度基本上(除了那个 log2nlog_2nlog2​n以外)与 nnn ...
一道虚树题
ACoder
04-30 351
虚树学习
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值