参考文章:
https://www.cnblogs.com/guoyaohua/p/8600214.html 十大经典排序算法最强总结(含JAVA代码实现)
https://mp.weixin.qq.com/s/gHjWM2eAyA4_kSRt4CMZmQ 归并排序就这么简单
归并排序分析:
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
| O(n*logn) | O(n*logn) | O(n*logn) | O(n) | Out-place | 稳定 |
归并排序原理:
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
归并排序算法描述:
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
算法原理图解:

Java代码实现:
代码一:
package com.sorting.algorithm;
import java.util.Arrays;
public class MergeSort {
public static int[] mergeSort(int[] array){
if(array.length<2)
return array;
int mid = array.length/2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
return merge(mergeSort(left),mergeSort(right));
}
private static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length+right.length];
for (int i=0, j=0, index=0; index < result.length; index++) {
if(i >= left.length){
result[index] = right[j]; j++;
}else if(j >= right.length){
result[index] = left[i]; i++;
}else if(left[i] < right[j]){
result[index] = left[i]; i++;
}else {
result[index] = right[j]; j++;
}
}
return result;
}
public static void printArr(int[] array){
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + ",");
}
System.out.println();
}
public static void main(String[] args) {
int[] array = { 58,26,10,32 };
System.out.println("排序之前:");
printArr(array);
System.out.println("-------------------------------");
System.out.println("排序过程");
int[] newArray = mergeSort(array);
System.out.println("-------------------------------");
System.out.println("排序之后:");
printArr(newArray);
}
}
代码二:
package com.sorting.algorithm;
public class MergeSort2 {
public static int[] mergeSort(int[] array,int L, int R){
// 如果只剩余一个元素,即L==R ,或者L>R 就返回
if(L >= R)
return array;
// 找到数组分割的中间数
int M = L+(R-L)/2;
// 对左边不断进行拆分
mergeSort(array, L, M);
// 对右边不断进行拆分
mergeSort(array, M+1, R);
// 返回两个有序数组的合并
return merge(array,L,M,R);
}
/*
* 2-路归并,归并两个已经排好序的数组
* L 数组起始部分
* M 数组中间部分
* R 数组结尾部分
*/
private static int[] merge(int[] array, int L, int M, int R) {
printArr(array);
// 左半部分数组
int[] leftArray = new int[M-L+1];
// 右半部分数组
int[] rightArray = new int[R-M];
// 将原数组左部分拷贝到左半部分数组中
for (int i = L; i <= M; i++) {
leftArray[i-L] = array[i];
}
// 将原数组右部分拷贝到右半部分数组中
for (int j = M+1; j <= R; j++) {
rightArray[j-M-1] = array[j];
}
/*
* i 为指向 leftArray 数组的模拟指针
* j 为指向 rightArray 数组的模拟指针
* k 为指向 array 数组的模拟指针
*/
int i=0,j=0,k=L;
// 比较左右两部分数组,哪个比较小,就放到原数组中
while(i < leftArray.length && j < rightArray.length){
if(leftArray[i] < rightArray[j]){
array[k] = leftArray[i];
k++;
i++;
}else{
array[k] = rightArray[j];
k++;
j++;
}
}
// 如果左半部分数组有剩余,就全部拷贝到原数组中
while(i < leftArray.length){
array[k] = leftArray[i];
k++;
i++;
}
// 如果右半部分数组有剩余,就全部拷贝到原数组中
while(j < rightArray.length){
array[k] = rightArray[j];
k++;
j++;
}
return array;
}
public static void printArr(int[] array){
for (int i = 0; i < array.length; i++) {
if(i != array.length-1)
System.out.print(array[i] + ",");
else
System.out.println(array[i]);
}
System.out.println();
}
public static void main(String[] args) {
int[] array = { 26,58,10,32,11,22,34,60 };
System.out.println("排序之前:");
printArr(array);
System.out.println("-------------------------------");
System.out.println("排序过程");
int[] newArray = mergeSort(array,0,array.length-1);
System.out.println("-------------------------------");
System.out.println("排序之后:");
printArr(newArray);
}
}
代码三:
package com.sorting.algorithm;
import java.util.Arrays;
public class MergeSort3 {
public static void mergeSort(int[] array, int l, int r) {
// 如果左部分只剩一个数,就返回
if(l >= r)
return ;
// 找到分隔数
int mid = (r+l)/2;
// 分隔左半部分,并继续分隔,直到最后剩一个数
mergeSort(array, l, mid);
// 分隔右半部分,并继续分隔,直到最后只剩下一个数
mergeSort(array, mid+1, r);
// 2-路归并,合并两个有序的数组
merge(array,l,mid,r);
}
/*
* 2-路归并
* 合并两个有序的数组,
* array: 是原数组
* l : 是分隔数组中的左起点
* mid : 是分隔左右的分隔下标
* r : 是分隔数组中的右终点
*/
private static void merge(int[] array, int l, int mid, int r) {
// 辅助数组
int[] aux = Arrays.copyOfRange(array, l, r+1);
// i 指向左半部分的起始 , j 指向右半部分的起始
int i=l, j=mid+1;
for (int k = l; k <= r; k++) {
if(i > mid){ // 如果左半部分已经添加完
array[k] = aux[j-l]; j++;
}
else if(j > r){ // 右半部分已经添加完
array[k] = aux[i-l]; i++;
}
else if(aux[i-l] <= aux[j-l]){ // 如果左半部分小于右半部分的数字
array[k] = aux[i-l]; i++;
}
else { // 如果右半部分的数字小于左半部分的数字
array[k] = aux[j-l]; j++;
}
}
}
public static void printArr(int[] array){
for (int i = 0; i < array.length; i++) {
if(i != array.length-1)
System.out.print(array[i] + ",");
else
System.out.println(array[i]);
}
System.out.println();
}
public static void main(String[] args) {
int[] array = { 58,36,70,22,88,64,1,32 };
System.out.println("排序之前:");
printArr(array);
System.out.println("-------------------------------");
System.out.println("排序过程");
mergeSort(array,0,array.length-1);
System.out.println("-------------------------------");
System.out.println("排序之后:");
printArr(array);
}
}
归并排序测试
代码一:
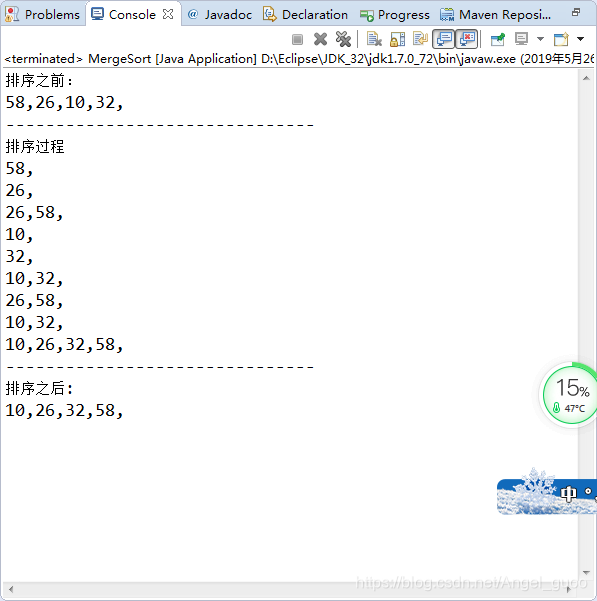
代码二:
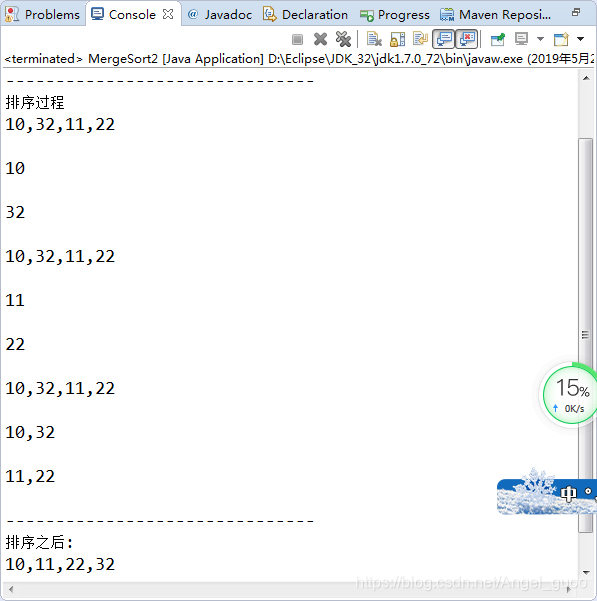
代码三:
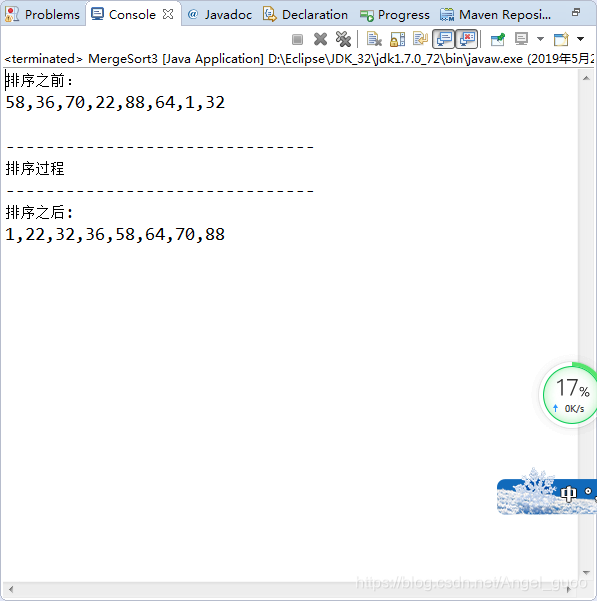










 归并排序是一种基于分治法的稳定排序算法,通过将两个有序子序列合并成一个完全有序序列。本文介绍了归并排序的原理、算法描述,并提供了多个Java代码实现示例,帮助读者理解和掌握这一经典排序方法。
归并排序是一种基于分治法的稳定排序算法,通过将两个有序子序列合并成一个完全有序序列。本文介绍了归并排序的原理、算法描述,并提供了多个Java代码实现示例,帮助读者理解和掌握这一经典排序方法。
















 64
64

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








