为什么这样求得的T和B,再加上N,为什么就能实现能把切线空间下的法向量转换成模型坐标系下的法向量?
这一点我没看到有文章能说清楚,这里我尝试按我的理解来解释下,重新强调一下我们的求解目标:求TBN坐标系的三个基向量,用它能把切线空间下的法向量转换成模型坐标系下的法向量。

我的思路是对于模型的某个三角形,把法向量纹理图按这个三角形的对应的纹理坐标对齐,再把T轴B轴分别与U轴V轴对齐,大概会得到上图第3个图那个样子,这时TBN坐标系就固定了下来,就是我们最终要求的,只是现在还不知道TBN三个坐标基是多少,然后我们把TBN坐标系及法向纹理图直接抽走,保留这个形态,得到上图最右边的样子。那么对于那个黄色三角形以及绿色的法向量来说,从上图第3个图到上图最右图的转换实际上就是从切线空间到模型坐标系的转换,转换的方法就是前面提到的线性代数知识点,将TBN坐标系下的坐标值,用TBN三个基在模型坐标系中对应的值来变换。
现在要求TBN,我们来列些式子,我们不知道绿色的法向量变换后的坐标,因为它就是我们最终想通过TBN变换求得的,但是我们知道黄色三角形变换后的坐标,也就是三角形对应的模型顶点在模型坐标系下的坐标,这样就能通过把TBN坐标系下的那个三角形变换到模型坐标系下的那个三角形建立变换等式,也就是前面这个式子:
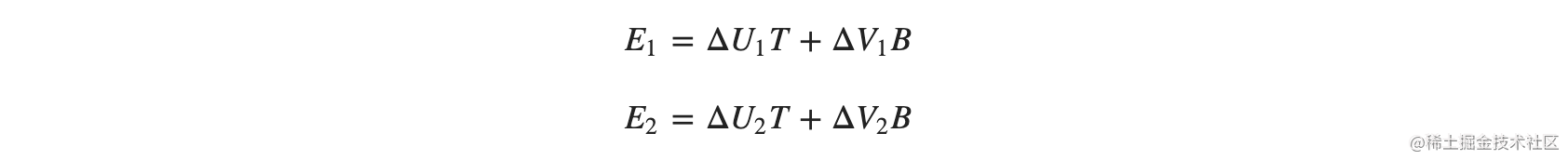
通过这两个式子就能求解出T和B:
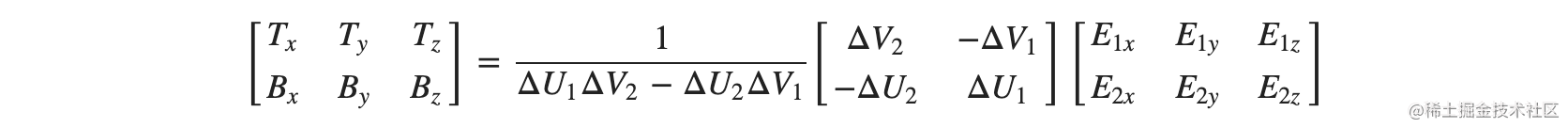





 本文介绍了如何通过提前计算TBN矩阵优化3D渲染中的法向量转换,以及如何将光照计算从模型坐标系转换到切线空间以减少fragment shader中的计算开销。详细解析了TBN坐标系的构建过程,并提到了glTF格式对tangent数据的支持。
本文介绍了如何通过提前计算TBN矩阵优化3D渲染中的法向量转换,以及如何将光照计算从模型坐标系转换到切线空间以减少fragment shader中的计算开销。详细解析了TBN坐标系的构建过程,并提到了glTF格式对tangent数据的支持。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1136
1136

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








