【必收藏】揭秘大模型“心里有数“的秘密：难度感知机制全解析

最新推荐文章于 2025-12-05 11:17:30 发布

原创最新推荐文章于 2025-12-05 11:17:30 发布 · 779 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #大模型入门 #大模型学习 #AI大模型 #LLM #大模型 #语言模型

前言

当大语言模型（LLM）面对一道数学题时，它是否能自己判断这道题是简单还是困难？更进一步，这种“难度感知”能力，是否真实存在于模型内部？又是否可以被我们定位、干预甚至利用？

近期，一篇题为《Probing the Difficulty Perception Mechanism of Large Language Models》的论文首次系统性地回答了这些问题。

一句话：大模型不仅能感知问题难度，而且这种感知是结构化的、可定位的，甚至藏在特定的注意力头里。

大模型的特定注意力头模式服务于难度感知

大模型也有“心里有数”的时候？

在自适应推理（比如根据题目难度动态调整思考长度）中，准确标注问题难度至关重要。但人工标注成本高、主观性强，代理指标如强模型的平均回答长度不一定准确，此外，基于熵的判别并没有解释模型的内在感知机制。

研究团队基于人工标注难度等级的极具挑战的数学问题数据集 DeepMath-103K（发布于 Qwen2.5 约半年后），在多个主流 LLM（如 Qwen2.5 系列）的最后一个输入 token 的隐藏表示上训练了一个轻量线性探针（linear probe）。实验表明：

该探针能以较高精度预测问题难度（MSE 损失稳定收敛，测试集表现良好）；
难度信息在高维嵌入空间中呈线性可分，但在低维可视化中难以区分
探针在分布外数据（仍为数学问题）上表现也符合预期，说明其具备一定泛化能力。

这表明，LLM 在接收到问题后、尚未开始生成答案前，其内部表示已隐式编码了对问题难度的判断。

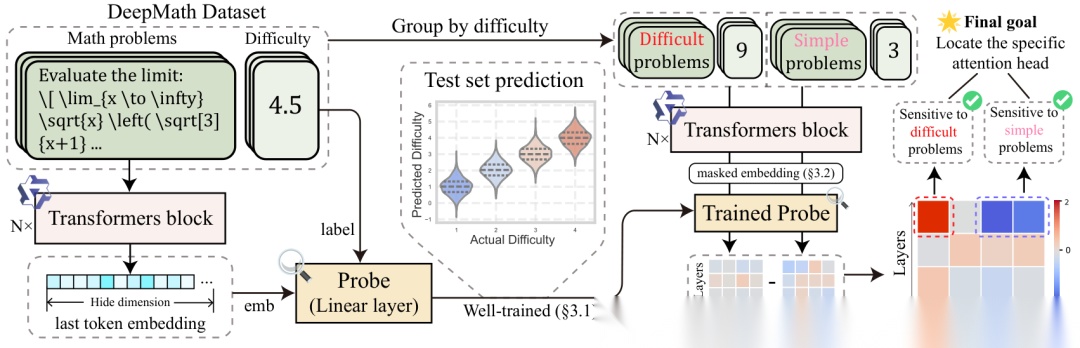
探针训练和注意力头模式识别。左侧演示了如何根据最后的令牌嵌入和相应的难度标签来训练难度探测器。右侧展示了使用探针识别注意力头模式的过程，其中困难问题的注意力头的难度分数减去简单问题的难度分数得到一个分化分数，用于定位对难度最敏感的注意力头。

方法详解：如何探测大模型的“难度感知”？

研究团队进一步定位到了负责难度感知的具体注意力头。这是通过注意力模块掩码消融实现的。

核心在于两个关键技术步骤：高维线性探针训练与注意力头模式识别。

1. 高维线性探针：难度感知存在于高维空间

尽管在低维可视化中，不同难度的数学题嵌入混杂难分，但是作者发现它们在高维空间上是线性的。

为此，他们在模型最后一个输入 token 的隐藏表示上训练一个轻量线性回归探针：

其中为预测难度，和为可学习参数。探针通过最小化均方误差优化：

实验表明，该探针不仅能准确拟合 DeepMath 数据集的人工难度标签，还能对分布外数据（如更简单的 GSM8K）给出合理低难度预测，验证了其泛化能力。

关键洞见：LLM 在尚未开始生成答案前，其内部表示已隐式编码了问题难度，且该编码在高维空间中呈线性结构。

2. 注意力头模式识别：定位“难度感知神经元”

为进一步定位难度感知的物理载体，作者采用一种基于注意力头消融的归因方法。

设为多头注意力输出，为输出投影矩阵，则最终表示为：

给定已训练好的难度探针方向，作者逐个屏蔽除第 i 个头外的所有注意力头，可以构造消融表示：

这样可以相应的得到，然后可以计算其对难度的贡献得分：

对“简单”与“困难”样本分别计算平均得分与，定义归因得分：

表示该头对难题更敏感（红色），则对简单题更敏感（蓝色）。如图 4 所示，Qwen2.5 系列模型在最后几层层呈现出清晰的“红蓝对立”模式。

通过计算不同难度样本下各头的归因得分差异，可清晰识别出具有判别性的“难度感知头”。在 Qwen2.5-7B 的最后一层 Transformer 中：

第 10–13 号注意力头：对简单题更敏感；
第 7、8、16、23 号注意力头：对难题更活跃。

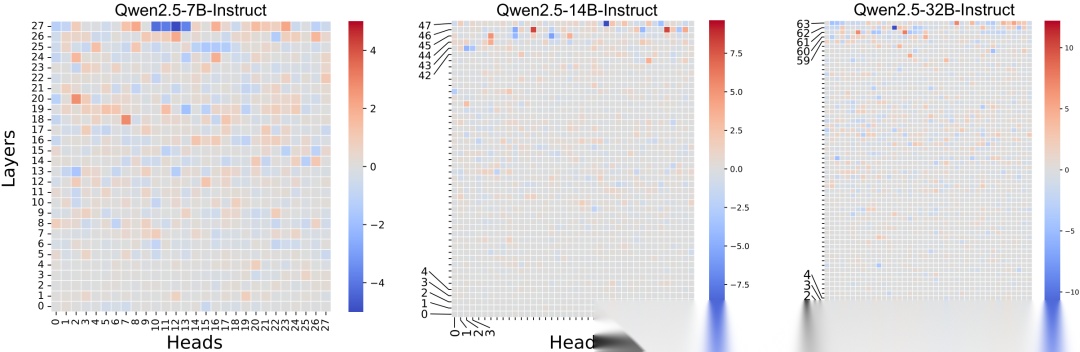
不同尺寸模型注意力头模式归因得分差异。图中展示了在显著难度差异下（9 级和 3 级）的方向。蓝色注意力头关注简单问题，而红色注意力头对应复杂问题识别。

3. 消融实验

因果验证：通过缩放这些头的输出（如将“简单头”×0.1、“难题头”×2.0），可显著操控模型对同一问题的难度判断（见原论文表 1），证实其功能性作用。

注意力头消融实验：

如果抑制“简单头”+ 增强“困难头” → 模型整体“觉得题目变难了”；
反之，则“觉得题目变简单了”。

这种因果干预证明：这些注意力头确实在功能性地编码难度感知。

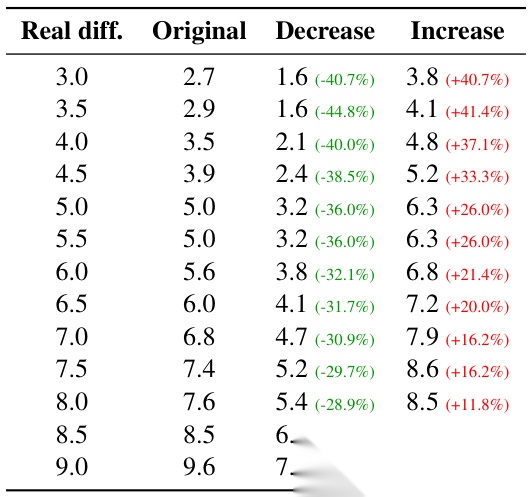
不同调整条件下的预测难度。Real diff. 表示 DeepMath 手动标注的难度标签。Original 指在未进行干预时，探针输出的平均难度估计；而 Decrease 代表抑制特定注意力头的难度感知，Increase 则表示相应的增强。

难度感知 ≠ 不确定性

大家原本困难认为模型输出越“犹豫”（即熵越高），题目就越难。但研究发现：

token 级别的难度感知与熵不一致。

例如：当模型生成数字时，虽然它非常确定（熵接近 0），但探针显示此时难度感知答复提高——研究者猜测这是因为数字一旦出错，后续推理容易全错。

作者承认，模型对一个问题的输出的熵越高，表明模型的不确定性越强，通常问题也确实越难，但这似乎不完全代表模型所认为的难易。

token 级别基于所提出的难度感知方法判别难度

token 级别基于熵的不确定性判别

并非所有模型都“心里有数”

有趣的是，Llama3.1-8B-Instruct 几乎没有明显的难度感知头，而经过蒸馏的 DeepSeek-R1 模型出现了感知头功能反转的情况。

这表明预训练和后训练质量都会显著影响模型是否具备清晰的难度感知机制。

未来工作

这项发现不仅有理论意义，更有许多继续探索的空间：

自动难度标注：用训练好的探针为新题目打难度标签，省去人工成本；
构建高质量基准：用于课程学习、自适应推理训练；
控制推理行为：动态调整 token 预算，避免“简单题啰嗦、难题放弃”。
开放问题的难度评估：关于数学问题的难度评估已经有许多工作，但开放问题的评估仍然值得讨论。

结语

该工作首次证明：大语言模型不仅能感知问题难度，而且这种感知是结构化、可定位、可干预的。它打破了“LLM 是黑箱”的刻板印象，展示了通过机制可解释性工具深入理解模型内部运作的可能性。

大模型不只是“黑箱”——它有自己的“难易判断标准”。

最后

为什么要学AI大模型

当下，⼈⼯智能市场迎来了爆发期，并逐渐进⼊以⼈⼯通⽤智能（AGI）为主导的新时代。企业纷纷官宣“ AI+ ”战略，为新兴技术⼈才创造丰富的就业机会，⼈才缺⼝将达 400 万！

DeepSeek问世以来，生成式AI和大模型技术爆发式增长，让很多岗位重新成了炙手可热的新星，岗位薪资远超很多后端岗位，在程序员中稳居前列。

在这里插入图片描述

与此同时AI与各行各业深度融合，飞速发展，成为炙手可热的新风口，企业非常需要了解AI、懂AI、会用AI的员工，纷纷开出高薪招聘AI大模型相关岗位。
在这里插入图片描述
最近很多程序员朋友都已经学习或者准备学习 AI 大模型，后台也经常会有小伙伴咨询学习路线和学习资料，我特别拜托北京清华大学学士和美国加州理工学院博士学位的鲁为民老师给大家这里给大家准备了一份涵盖了AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频 全系列的学习资料，这些学习资料不仅深入浅出，而且非常实用，让大家系统而高效地掌握AI大模型的各个知识点。