LeetCode 98. 验证二叉搜索树 (递归)

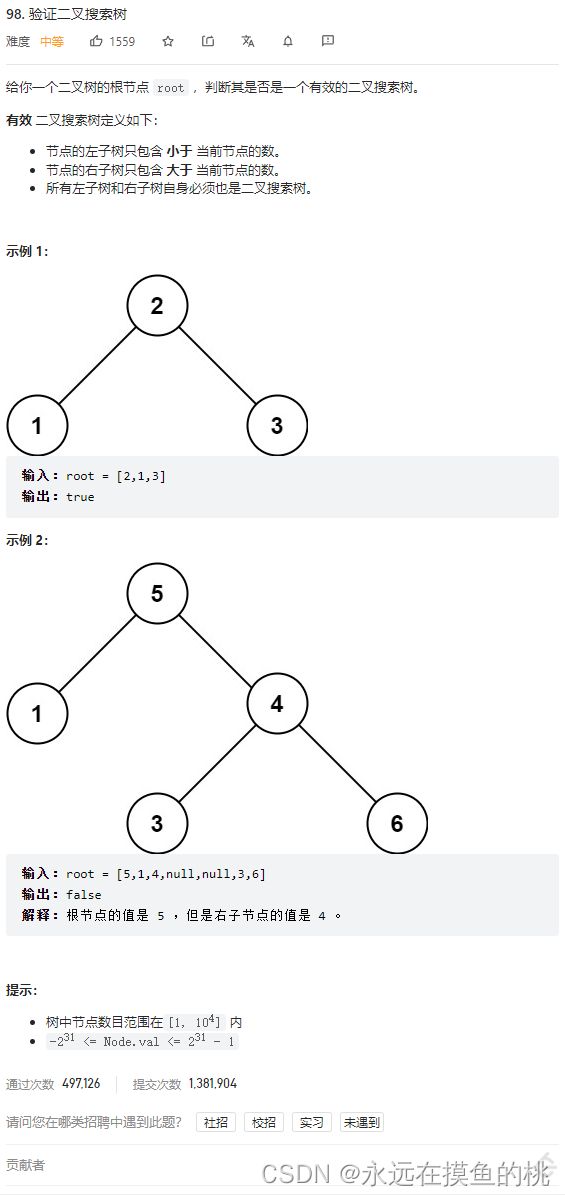
思路

利用二叉搜索树的特性，左子树均小于根节点，右子树均大于根节点；
所以我们利用一个函数，传入一个节点的左右子树，以及它所对应的最大值和最小值；

1. 对于左子树，最小值为空，最大值就是当前根节点的值
2. 对于右子树，最大值为空，最小值就是当前根节点的值

根据这个规律，依次递归的查找每个节点的左右子树，是否在其对应的范围之内，如果最后到达叶子结点都符合，说明是二叉搜索树，返回true；只要有一个不符合，就返回false

代码实现(java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return isBST(root, null, null);
    }

    public boolean isBST(TreeNode root, TreeNode min, TreeNode max) {
        if(root == null) return true;
        // 如果这个节点，小于等于了自己的左子树根节点，或者大于等于了右子树根节点，说明不是二叉搜索树
        if(min != null && root.val <= min.val) return false;
        if(max != null && root.val >= max.val) return false; 
    
        return isBST(root.left, min, root) && isBST(root.right, root, max);
    }
}